湖南省娄底市2023年中考模拟数学考试试卷 (5月份)
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的倒数是( )A、 B、 C、 D、2. 下面的计算正确的是( )A、 B、 C、 D、3. 九年级班的名同学参加学校举办的青少年图书教育活动讲故事比赛,他们的成绩单位:分分别是 , , , , , 这组数据的中位数和平均数分别为( )A、 , B、 , C、 , D、 ,4. 党的二十大报告中指出,我国全社会研发经费支出从一万亿元增加到二万八千亿元,居世界第二位,研发人员总量居世界首位.将2800000000000用科学记数法表示为( )A、0.28×1013 B、2.8×1011 C、2.8×1012 D、28×10115. 中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )A、
 中国探火
中国探火
B、 中国探月
中国探月
C、 中国行星探测
中国行星探测
D、 中国火箭
6. 光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且 , 则( )
中国火箭
6. 光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且 , 则( ) A、 B、 C、 D、7. 下列命题中,假命题是( )A、若的三边满足 , 则是直角三角形
A、 B、 C、 D、7. 下列命题中,假命题是( )A、若的三边满足 , 则是直角三角形
B、顺次连接任意四边形各边中点得到的四边形是平行四边形
C、对角线互相垂直平分的四边形是菱形
D、对角线相等且垂直的四边形是正方形8. 如图,下列解析式能表示图中变量 , 之间关系的是( ) A、
A、
B、
C、
D、9. 如图,为的切线,切点为 , 连接、 , 交于点 , 点在上,连接、 , 若 , , 则的长为( ) A、 B、 C、 D、10. 如图,抛物线与直线交于 , 两点,则不等式的解集为( )
A、 B、 C、 D、10. 如图,抛物线与直线交于 , 两点,则不等式的解集为( )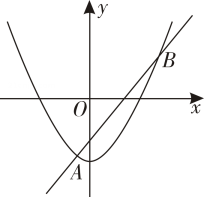 A、
A、
B、
C、
D、或11. 如图,中, , , 点是边上的动点,过点作于点 , 于点 , 则的长是( ) A、 B、 C、或 D、12. 若“”是一种数学运算符号,并且 , , , , 且公式 , 则( )A、 B、 C、 D、
A、 B、 C、或 D、12. 若“”是一种数学运算符号,并且 , , , , 且公式 , 则( )A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
13. 函数y= 中自变量x的取值范围是 .14. 若 , 则 .15. 如图,把沿平行于的直线折叠,使点落在边上的点处,若 , 则的度数为 .
 16. 如图,正方形内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称现随机的向该图形内投掷一枚小针,则针尖落在正方形内切圆中黑色部分的概率为 .
16. 如图,正方形内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称现随机的向该图形内投掷一枚小针,则针尖落在正方形内切圆中黑色部分的概率为 . 17. 某几何体的三视图如图所示,根据图中数据可得,该几何体的侧面积为 .
17. 某几何体的三视图如图所示,根据图中数据可得,该几何体的侧面积为 . 18. 如图,在矩形中,将绕点逆时针旋转得到 , 使得、、三点恰好在同一直线上,与相交于点 , 连接 , 以下结论正确的是: .
18. 如图,在矩形中,将绕点逆时针旋转得到 , 使得、、三点恰好在同一直线上,与相交于点 , 连接 , 以下结论正确的是: .;∽;点是线段的黄金分割点; .

三、解答题(本大题共8小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算: .20. 先化简,再求值: , 其中是满足条件的合适的正整数.21. 湖南省作为全国第三批启动高考综合改革的省市之一,从年秋季入学的高中一年级学生开始实施高考综合改革为了了解我县某小区居民对此政策的关注程度,某数学兴趣小组随机采访了该小区部分居民,根据采访情况制做了统计图表:根据统计图表,解答下列问题:
关注程度
频数
频率
A.高度关注
B.一般关注
C.没有关注
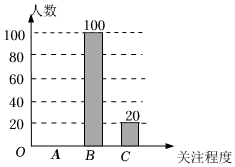 (1)、此次采访的居民人数为 , , ;
(1)、此次采访的居民人数为 , , ;
(2)、根据以上信息补全图中的条形统计图;
(3)、请估计在该小区名居民中,高度关注新高考政策的约有多少人?22. 为了测量高速公路某桥的桥墩高度,某数学兴趣小组在同一水平地面、两处实地测量,如图所示在处测得桥墩顶部处的仰角为和桥墩底部处的俯角为 , 在处测得桥墩顶部处的仰角为 , 测得、两点之间的距离为 , 直线、在同一平面内,请你用以上数据,求桥墩的高度. 23. 广西平陆运河北起横州市西津水电站库区平塘江口,南止于钦江出海口沙井港航道,在一航道建设中,某渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方已知辆大型渣土运输车与辆小型渣土运输车一次共运输土方吨,辆大型渣土运输车与辆小型渣土运输车一次共运输土方吨.(1)、一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
23. 广西平陆运河北起横州市西津水电站库区平塘江口,南止于钦江出海口沙井港航道,在一航道建设中,某渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方已知辆大型渣土运输车与辆小型渣土运输车一次共运输土方吨,辆大型渣土运输车与辆小型渣土运输车一次共运输土方吨.(1)、一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)、该渣土运输公司决定派出大、小两种型号渣土运输车共辆参与把吨土方全部运走,若一辆大型渣土运输车耗费元,一辆小型渣土运输车耗费元,请你设计出最省钱的运输方案.24. 如图,在平行四边形中,对角线 , 相交于点 , , 点是的中点,过点作 , 交于点 .
 (1)、求证:四边形是矩形;
(1)、求证:四边形是矩形;
(2)、若 , 矩形的面积为 , 请直接写出的值.

