北京市顺义区2023年中考二模数学考试试卷

试卷更新日期：2023-10-09 类型：中考模拟

进入出卷网下载

一、选择题（本大题共8小题，共16.0分。在每小题列出的选项中，选出符合题目的一项）

1. 如图是某几何体的侧面展开图，该几何体是（）

A、圆柱
B、圆锥
C、三棱柱
D、长方体

查看试题解析
2. $4$ 月 $23$ 日是世界读书日 $. 2023$ 北京书市以“书香京城 $\cdot$ 悦读春天”为主题，于 $4$ 月 $14$ 日至 $4$ 月 $24$ 日在主展区内集中展示展销超过 $40$ 万种优秀出版物及文化产品，满足民众多样化高品质的阅读文化需求，将 $400000$ 用科学记数法表示应为（）

A、 $0.4 \times 1 0^{6}$ B、 $4 \times 1 0^{5}$ C、 $40 \times 1 0^{4}$ D、 $4 \times 1 0^{4}$

查看试题解析
3. 如图，为了加固房屋，要在屋架上加一根横梁 $D E$ ，使 $D E / / B C$ .若 $∠ A B C = 30 °$ ，则 $∠ B D E$ 的度数是（）

A、 $30 °$ B、 $60 °$ C、 $120 °$ D、 $150 °$

查看试题解析
4. 实数 $a$ 在数轴上的对应点的位置如图所示，若实数 $b$ 满足 $- b < | a | < b$ ，则 $b$ 的值可以是（）

A、 $2$ B、 $1$ C、 $0$ D、 $- 1$

查看试题解析
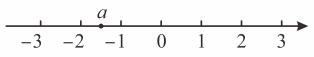5. 下列图形既是轴对称图形，又是中心对称图形的是（）

A、 B、
C、 D、

查看试题解析
6. 某餐饮外卖平台规定，点单时除点餐费用外，需另付配送费 $9$ 元 $.$ 某学习小组收集了一段时间内该外卖平台的部分订单，统计了每单的消费总额和每单不计算配送费的消费额的两组数据，对于这两组数据，下列判断正确的是（）

A、众数相同 B、中位数相同 C、平均数相同 D、方差相同

查看试题解析
7. 如图，要测量楼高 $M N$ ，在距 $M N$ 为 $15 m$ 的点 $B$ 处竖立一根长为 $5.5 m$ 的直杆 $A B$ ，恰好使得观测点 $E$ 、直杆顶点 $A$ 和高楼顶点 $N$ 在同一条直线上，若 $D B = 5 m$ ， $D E = 1.5 m$ ，则楼高 $M N$ 是（）

A、 $13.5 m$
B、 $16.5 m$
C、 $17.5 m$
D、 $22 m$

查看试题解析
8. 某超市一种干果现在的售价是每袋 $30$ 元，每星期可卖出 $100$ 袋，经市场调研发现，如果在一定范围内调整价格，每涨价 $1$ 元，每星期就少卖出 $5$ 袋，已知这种干果的进价为每袋 $20$ 元，设每袋涨价 $x ($ 元 $)$ ，每星期的销售量为 $y ($ 袋 $)$ ，每星期销售这种干果的利润为 $z ($ 元 $) .$ 则 $y$ 与 $x$ ， $z$ 与 $x$ 满足的函数关系分别是（）

A、一次函数，二次函数 B、一次函数，反比例函数
C、反比例函数，二次函数 D、反比例函数，一次函数

查看试题解析

二、填空题（本大题共8小题，共16.0分）

9. 若分式 $\frac{x - 2}{x - 1}$ 的值为 $0$ ，则 $x$ 的值为．

查看试题解析
10. 五边形的内角和是°．

查看试题解析
11. 在平面直角坐标系 $x O y$ 中，若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $A (1 ， 3)$ 和点 $B (- 3 ， n)$ ，则 $n$ 的值为．

查看试题解析
12. 如果 $a - b = 3$ ，那么代数式 $(1 - \frac{a}{a + b}) \cdot \frac{a^{2} - b^{2}}{b}$ 的值为．

查看试题解析
13. 如图，在 $△ A B C$ 中， $A D$ ， $B D$ 分别是 $∠ B A C$ ， $∠ A B C$ 的平分线，过点 $D$ 作 $E F / / A B$ ，分别交 $A C$ ， $B C$ 于点 $E$ ， $F .$ 若 $A E = 4$ ， $B F = 6$ ，则 $E F$ 的长为．

查看试题解析
14. 不透明的袋子中有四个完全相同的小球，上面分别写着数字 $1$ ， $2$ ， $3$ ， $4 .$ 随机摸出一个小球，记录其数字，放回并摇匀，再随机摸出一个小球，记录其数字，则两次记录的数字不相同的概率是．

查看试题解析
15. 如图，将矩形纸片 $A B C D$ 折叠，使点 $B$ 与 $C D$ 边的中点 $E$ 重合，折痕恰好为 $A F$ ，则 $\frac{C F}{B F}$ 的值为．

查看试题解析
16. 在一次数学活动课上，李老师将一副扑克牌中的红桃 $2 ～ 10$ 共 $9$ 张牌挑出，打乱顺序随机发给了甲、乙、丙三名同学，每人三张牌 $.$ 已知甲的三张牌数字之和是 $12$ ，乙的三张牌数字之和与丙的三张牌数字之和相同，且乙的三张牌上的数字都是奇数 $.$ 写出甲的三张牌上的数字是，丙的三张牌上的数字是．

查看试题解析

三、解答题（本大题共12小题，共68.0分。解答应写出文字说明，证明过程或演算步骤）

17. 计算： $(π - 4)^{0} + | - \sqrt{2} | - 2 c o s 60 ° - \sqrt{18}$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 3 x - 4 > 2 - 3 x \\ \frac{4 x + 3}{5} > - 1 \end{array}$ ．

查看试题解析
19. 已知：线段 $A B$ 及射线 $A M .$ 求作：等腰 $△ A B C$ ，使得点 $C$ 在射线 $A M$ 上．
作法一：如图 $1$ ，以点 $B$ 为圆心， $B A$ 长为半径作弧，交射线 $A M$ 于点 $C ($ 不与点 $A$ 重合 $)$ ，连接 $B C$ ．
作法二：如图 $2$ ，
$①$ 在 $A B$ 上取一点 $D$ ，以点 $A$ 为圆心， $A D$ 长为半径作弧，交射线 $A M$ 于点 $E$ ，连接 $D E$ ；
$②$ 以点 $B$ 为圆心， $A D$ 长为半径作弧，交线段 $B A$ 于点 $F$ ；
$③$ 以点 $F$ 为圆心， $D E$ 长为半径作弧，交前弧于点 $G$ ；
$④$ 作射线 $B G$ 交射线 $A M$ 于点 $C$ ．
作法三：如图 $3$ ，
$①$ 分别以点 $A$ ， $B$ 为圆心，大于 $\frac{1}{2} A B$ 的同样长为半径作弧，两弧分别交于点 $P$ ， $Q$ ；
$②$ 作直线 $P Q$ ，交射线 $A M$ 于点 $C$ ，连接 $B C$ ．
根据以上三种作法，填空：由作法一可知：▲   $= A B$ ， $∴ △ A B C$ 是等腰三角形；
由作法二可知： $∠$      ▲ $= ∠ B A M$ ， $∴ C A = C B （） ($ 填推理依据 $)$ ， $∴ △ A B C$ 是等腰三角形；
由作法三可知： $P Q$ 是线段 $A B$ 的▲   $∴ C A = C B （） ($ 填推理依据 $) ∴ △ A B C$ 是等腰三角形．

查看试题解析
20. 已知关于 $x$ 的方程 $x^{2} - b x + 2 b - 4 = 0$ ．

(1)、求证：方程总有两个实数根；

(2)、若 $b$ 为正整数，且方程有一个根为负数，求 $b$ 的值．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $A$ 关于 $B C$ 的对称点为 $D$ ，连接 $B D$ ， $C D$ ．

(1)、求证：四边形 $A B D C$ 是菱形；

(2)、过点 $A$ 作 $A E ⊥ B D$ 于 $E$ ，且交 $B C$ 于点 $F$ ，若 $A B = 6$ ， $B E = 4$ ，求 $A F$ 的长．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b (k \neq 0)$ 的图象由 $y = - 2 x$ 的图象平移得到，且过点 $(2 ， - 1)$ ．

(1)、求这个一次函数的解析式；

(2)、当 $x > 2$ 时，对于 $x$ 的每一个值，函数 $y = m x (m \neq 0)$ 的值大于函数 $y = k x + b (k \neq 0)$ 的值，直接写出 $m$ 的取值范围．

查看试题解析
23. 在某次男子三米跳板比赛中，每名参赛选手要进行六轮比赛，每轮得分的计算方式如下，

如图是对参加比赛的甲、乙、丙三位选手的得分数据进行了整理，描述和分析，给出部分信息：
$a .$ 甲、丙两位选手的得分折线图：

$b .$ 乙选手六轮比赛的得分： $74.5$ ， $68.6$ ， $96.9$ ， $m$ ， $63.25$ ， $92.75$ ；
$c .$ 甲、乙、丙三位选手六轮比赛得分的平均数：
选手
甲
乙
丙
平均数
          $85.55$
     $n$
          $82.55$
根据以上信息，回答下列问题：

(1)、已知乙选手第四轮动作的难度系数为 $3.5$ ，七名裁判的打分分别为： $8.0$ ， $8.0$ ， $8.5$ ， $8.0$ ， $8.0$ ， $8.0$ ， $7.5$ ，求乙选手第四轮比赛的得分 $m$ 及表中 $n$ 的值；

(2)、从甲、丙两位选手的得分折线图中可知，选手     ▲     发挥的稳定性更好 $($ 填“甲”或丙” $)$ ；

(3)、每名选手六轮比赛得分的总和为个人最终得分，根据上述信息判断：在甲、乙、丙三位选手中，最终得分最高的是     ▲    $($ 填“甲”“乙”或“丙” $)$ ．

查看试题解析
24. 如图， $P A$ ， $P B$ 分别与 $⊙ O$ 相切于 $A$ ， $B$ 两点， $A C$ 是 $⊙ O$ 的直径．

(1)、求证： $∠ B A C = \frac{1}{2} ∠ A P B$ ；

(2)、连接 $P O$ 交 $⊙ O$ 于点 $D$ ，若 $A C = 6$ ， $c o s ∠ B A C = \frac{4}{5}$ ，求 $P D$ 的长．

查看试题解析

25. 某架飞机着陆后滑行的距离

y (

单位：

m)

与滑行时间

x (

单位：

s)

近似满足函数关系

y = a x^{2} + b x (a \neq 0)

，由电子监测获得滑行时间

x

与滑行距离

y

的几组数据如表：

滑行时间 $x / s$	$0$	$2$	$4$	$6$	$8$	$10$
滑行距离 $y / m$	$0$	$114$	$216$	$306$	$384$	$450$

(1)、根据上述数据，求出满足的函数关系

y = a x^{2} + b x (a \neq 0)

；

(2)、飞机着陆后滑行多远才能停下来？此时滑行的时间是多少？

查看试题解析

26. 在平面直角坐标系 $x O y$ 中，已知抛物线 $y = a x^{2} - 2 a^{2} x - 3 (a \neq 0)$ ．

(1)、求该抛物线的对称轴 $($ 用含 $a$ 的式子表示 $)$ ；

(2)、若 $a = 1$ ，当 $- 2 < x < 3$ 时，求 $y$ 的取值范围；

(3)、已知 $A (2 a - 1 ， y_{1})$ ， $B (a ， y_{2})$ ， $C (a + 2 ， y_{3})$ 为该抛物线上的点，若 $y_{1} < y_{3} < y_{2}$ ，求 $a$ 的取值范围．

查看试题解析
27. 已知： $∠ A B C = 120 °$ ， $D$ ， $E$ 分别是射线 $B A$ ， $B C$ 上的点，连接 $D E$ ，以点 $D$ 为旋转中心，将线段 $D E$ 绕着点 $D$ 逆时针旋转 $60 °$ ，得到线段 $D F$ ，连接 $E F$ ， $B F$ ．

(1)、如图 $1$ ，当 $B D = B E$ 时，求证： $B F = 2 B D$ ；

(2)、当 $B D \neq B E$ 时，依题直补全图 $2$ ，用等式表示线段 $B D$ ， $B F$ ， $B E$ 之间的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，已知点 $P$ ，直线 $l$ 与图形 $G .$ 连接点 $P$ 与图形 $G$ 上任意一点 $Q$ ，取 $P Q$ 的中点 $M$ ，点 $M$ 关于直线 $l$ 的对称点为 $N$ ，所有的对称点组成的图形 $W$ 称为图形 $G$ 关于点 $P$ 及直线 $l$ 的“对应图形” $.$ 已知点 $A (4 ， 0)$ ．

(1)、对于直线 $l$ ： $x = a$ ，若直线 $y = - 2 x - 4$ 关于点 $A$ 及直线 $l$ 的“对应图形”与直线 $y = - 2 x - 4$ 的交点在 $x$ 轴的上方，求 $a$ 的取值范围；

(2)、已知点 $B (0 ， 4)$ ， $C (- 4 ， 0)$ ， $D (6 ， 4)$ ，直线 $l$ ： $x = - 1$ ， $⊙ T$ 的圆心 $T (t ， 0)$ ，半径为 $2 .$ 若存在 $⊙ T$ 关于点 $D$ 及直线 $l$ 的“对应图形“与 $△ A B C$ 的边有交点，直接写出 $t$ 的取值范围．

查看试题解析

选手	甲	乙	丙
平均数	$85.55$	$n$	$82.55$