北京市延庆区2023年中考一模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共8小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列几何体的主视图和俯视图完全相同的是( )A、
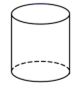 B、
B、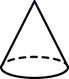 C、
C、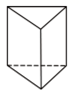 D、
D、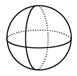 2. 2022年6月5日,中华民族再探苍穹,神舟十四号载人飞船通过长征二号F运载火箭成功升空,并与天和核心舱顺利进行接轨.据报道,长征二号F运载火箭的重量大约是500000kg.将数据500000用科学记数法表示,结果是( )A、5×105 B、5×106 C、0.5×105 D、0.5×1063. 下列图形中,是中心对称图形的是( )A、
2. 2022年6月5日,中华民族再探苍穹,神舟十四号载人飞船通过长征二号F运载火箭成功升空,并与天和核心舱顺利进行接轨.据报道,长征二号F运载火箭的重量大约是500000kg.将数据500000用科学记数法表示,结果是( )A、5×105 B、5×106 C、0.5×105 D、0.5×1063. 下列图形中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 不透明的袋子中装有一个红色小球和一个白色小球,除颜色外两个小球无其他差别从中随机取出一个小球后,放回并摇匀,再从中随机取出一个小球,则两次都取到白色小球的概率为( )A、 B、 C、 D、5. 实数a,b在数轴上的对应点的位置如图所示,则下列结论中,正确的是( )
4. 不透明的袋子中装有一个红色小球和一个白色小球,除颜色外两个小球无其他差别从中随机取出一个小球后,放回并摇匀,再从中随机取出一个小球,则两次都取到白色小球的概率为( )A、 B、 C、 D、5. 实数a,b在数轴上的对应点的位置如图所示,则下列结论中,正确的是( )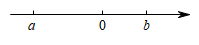 A、 B、 C、 D、6. 如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是( )
A、 B、 C、 D、6. 如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是( )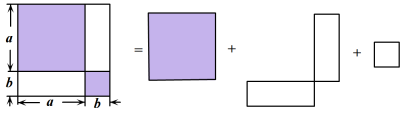 A、 B、 C、 D、7. 如图是作线段垂直平分线的作图痕迹,则下列结论不一定成立的是( )
A、 B、 C、 D、7. 如图是作线段垂直平分线的作图痕迹,则下列结论不一定成立的是( ) A、
A、
B、
C、
D、8. 如图,用绳子围成周长为的矩形,记矩形的一边长为 , 它的邻边长为当在一定范围内变化时,随的变化而变化,则与满足的函数关系是( ) A、一次函数关系 B、二次函数关系 C、正比例函数关系 D、反比例函数关系
A、一次函数关系 B、二次函数关系 C、正比例函数关系 D、反比例函数关系二、填空题(本大题共8小题,共16.0分)
-
9. 若 在实数范围内有意义,则实数x的取值范围是 .10. 分解因式: =11. 方程组的解为 .12. 如图,的弦 , 相交于点若 , , 则
 13. 如图,在中,点 , 分别在边 , 上,且 , 若 , , 的面积是 , 则的面积是 .
13. 如图,在中,点 , 分别在边 , 上,且 , 若 , , 的面积是 , 则的面积是 . 14. 如图,在中,点 , 将向左平移个单位得到 , 再向下平移个单位得到 , 则点的对应点的坐标为 .
14. 如图,在中,点 , 将向左平移个单位得到 , 再向下平移个单位得到 , 则点的对应点的坐标为 . 15. 在平面直角坐标系中,点 , 在反比例函数的图象上,且 , 请你写出一个符合要求的的值 .16. 甲、乙两种物质的溶解度与温度之间的对应关系如图所示,下列说法中,
15. 在平面直角坐标系中,点 , 在反比例函数的图象上,且 , 请你写出一个符合要求的的值 .16. 甲、乙两种物质的溶解度与温度之间的对应关系如图所示,下列说法中,
甲、乙两种物质的溶解度均随着温度的升高而增大;
当温度升高至时,甲的溶解度比乙的溶解度小;
当温度为时,甲、乙的溶解度都小于;
当温度为时,甲、乙的溶解度相同.
所有正确结论的序号是 .三、计算题(本大题共2小题,共10.0分)
-
17. 计算: .18. 解不等式组
四、解答题(本大题共10小题,共58.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 已知 , 求代数式的值.20. 已知关于的一元二次方程 .
(1)、求证:方程总有两个实数根;
(2)、如果方程有一个根为正数,求的取值范围.21. 如图,在平行四边形中,连接 , 点为边的中点,连接并延长,交的延长线于点 , 连接 . (1)、求证:四边形是矩形;
(1)、求证:四边形是矩形;
(2)、若 , , 求四边形的面积.22. 在平面直角坐标系中,一次函数的图象由正比例函数的图象平移得到,且经过点 .(1)、求 , 的值;
(2)、当时,对于的每一个值,函数的值小于一次函数的值,直接写出的取值范围.23. 如图,是的外接圆,是的直径, , 且 . (1)、求证:是的切线;
(1)、求证:是的切线;
(2)、若 , , 求的半径.24. 原地正面掷实心球是北京市初中学业水平考试体育现场考试的选考项目之一实心球被掷出后的运动路线可以看作是抛物线的一部分如图所示,建立平面直角坐标系 , 实心球从出手到落地的过程中,它的竖直高度单位:与水平距离单位:近似满足函数关系 .
小明训练时,实心球的水平距离与竖直高度的几组数据如下:
水平距离
竖直高度
根据上述数据,解决下列问题:
(1)、直接写出实心球竖直高度的最大值是 ;
(2)、求出满足的函数关系;
(3)、求实心球从出手到落地点的水平距离.25. 为了增强同学们的消防安全意识,普及消防安全知识,提高自防自救能力,某中学开展了形式多样的培训活动为了解培训效果,该校组织七、八年级全体学生参加了消防知识竞赛百分制 , 并规定分及以上为优秀,分为良好,分为及格,分及以下为不及格学校随机抽取了七、八年级各名学生的成绩进行了整理与分析,下面给出了部分信息.
抽取七年级名学生的成绩如下:
抽取七年级名学生成绩的频数分布直方图如图:
数据分成组: , , , ,
抽取八年级名学生成绩的扇形统计图:
七年级、八年级各抽取的名学生成绩的平均数、中位数如表:年级
平均数
中位数
七年级
八年级
请根据以上信息,完成下列问题:
(1)、补全七年级名学生成绩的频数分布直方图,写出表中的值;
(2)、该校八年级有学生人,估计八年级测试成绩达到优秀的学生有多少人?
(3)、在七年级抽取的学生成绩中,高于他们平均分的学生人数记为;在八年级抽取的学生成绩中,高于他们平均分的学生人数记为比较 , 的大小,并说明理由.26. 在平面直角坐标系中,点在抛物线上. (1)、当时,求的值;(2)、点在抛物线上,若存在 , 使得 , 直接写出的取值范围.27. 如图,在中, , , 是边上的高,点是边上的一动点不与点 , 重合 , 连接交于点将线段绕点顺时针旋转得到线段 , 连接 .
(1)、当时,求的值;(2)、点在抛物线上,若存在 , 使得 , 直接写出的取值范围.27. 如图,在中, , , 是边上的高,点是边上的一动点不与点 , 重合 , 连接交于点将线段绕点顺时针旋转得到线段 , 连接 .
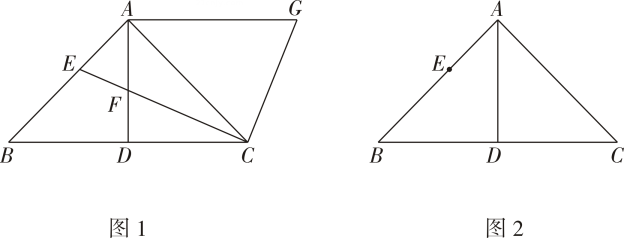 (1)、如图 , 当是的角平分线时,
(1)、如图 , 当是的角平分线时,
求证:;
直接写出(2)、依题意补全图 , 用等式表示线段 , , 之间的数量关系,并证明.28. 在平面直角坐标系中,的半径为对于线段和点点不在直线上 , 给出如下定义:过点作直线的平行线 , 如果线段关于直线的对称线段是的弦,那么线段称为的点对称弦.
 (1)、如图, , , , , , 在线段 , 中,的点对称弦是 ;
(1)、如图, , , , , , 在线段 , 中,的点对称弦是 ;
(2)、等边的边长为 , 点若线段是的点对称弦,求的值;
(3)、点在直线上,的半径为 , 过点作直线的垂线,交于点 , 若点在上,且线段是的点对称弦,直接写出点的横坐标的取值范围.