北京市通州区2023年2023年中考一模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共8小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列图形:线段;角;等边三角形;平行四边形其中既是轴对称图形又是中心对称图形的是( )A、 B、 C、 D、2. 年月国家统计局网站数据显示,年全国居民人均消费支出元,将用科学记数法表示( )A、 B、 C、 D、3. 如图,一副三角板拼成如图所示图形,则的度数为( )
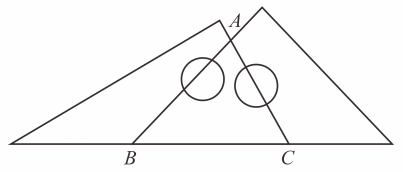 A、 B、 C、 D、4. 正七边形的外角和为( )A、 B、 C、 D、5. 如图是某个几何体的表面展开图,则这个几何体是( )
A、 B、 C、 D、4. 正七边形的外角和为( )A、 B、 C、 D、5. 如图是某个几何体的表面展开图,则这个几何体是( )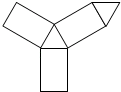 A、长方体 B、三棱柱 C、三棱锥 D、四棱锥6. 点 , 在数轴上的位置如图所示,点 , 表示的有理数为 , 如果 , , 那么下列描述数轴原点的位置说法正确的是( )
A、长方体 B、三棱柱 C、三棱锥 D、四棱锥6. 点 , 在数轴上的位置如图所示,点 , 表示的有理数为 , 如果 , , 那么下列描述数轴原点的位置说法正确的是( ) A、原点在点左侧 B、原点在点的右侧 C、原点在点、之间,且 D、原点在点、之间,且7. 如图 , 一个均匀的转盘被平均分成等份,分别标有 , , , , , , , , , 小凯转动转盘做频率估计概率的实验,当转盘停止转动后,指针指向的数字即为实验转出的数字,图 , 是小凯记录下的实验结果情况,那么小凯记录的实验是( )
A、原点在点左侧 B、原点在点的右侧 C、原点在点、之间,且 D、原点在点、之间,且7. 如图 , 一个均匀的转盘被平均分成等份,分别标有 , , , , , , , , , 小凯转动转盘做频率估计概率的实验,当转盘停止转动后,指针指向的数字即为实验转出的数字,图 , 是小凯记录下的实验结果情况,那么小凯记录的实验是( )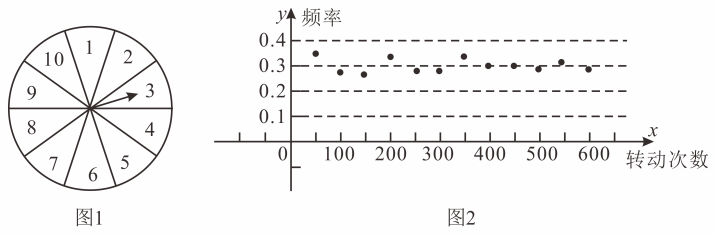 A、转动转盘后,出现偶数 B、转动转盘后,出现能被整除的数
A、转动转盘后,出现偶数 B、转动转盘后,出现能被整除的数
C、转动转盘后,出现比大的数 D、转动转盘后,出现能被整除的数8. 如图,在平面直角坐标系中,四边形是一个矩形,小球从点出发沿直线向点运动,到达点时被第一次反弹,每当小球沿直线运动碰到矩形的边时反弹,反弹时反射角等于入射角,当小球第次碰到矩形的边时,小球所在位置的坐标为( )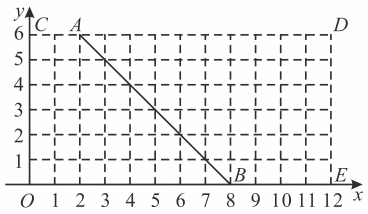 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共16.0分)
-
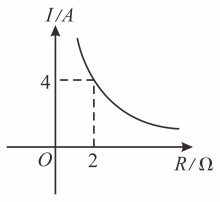
9. 若代数式有意义,那么的取值范围是 .10. 分解因式 .11. 已知为整数,且 , 则等于 .12. 方程的解是 .13. 由电源、开关、滑动变阻器及若干导线组成的串联电路中,已知电源电压为定值,闭合开关后,改变滑动变阻器的阻值始终保持 , 发现通过滑动变阻器的电流与滑动变阻器的电阻成反比例函数关系,它的图象如图所示,若使得通过滑动变阻器的电流不超过 , 则滑动变阻器阻值的范围是 .
 14. 为探究浸种处理对花生种子萌发率的影响,九年级的生物小组同学取粒花生种子完成实验同学们将粒花生种子平均分成五组,获得如下花生种子萌发量数据,如表格.
14. 为探究浸种处理对花生种子萌发率的影响,九年级的生物小组同学取粒花生种子完成实验同学们将粒花生种子平均分成五组,获得如下花生种子萌发量数据,如表格.组别
处理花生种子萌发量单位:粒
第组
第组
第组
第组
第组
浸种小时、
在温度的条件下,将粒种子浸种小时,萌发量大致为 粒
15. 在中, , , 将一个直角尺的直角顶点与边上的中点重合,并绕点旋转,分别交、于点、 , 如果四边形恰巧是正方形,则的长度为 .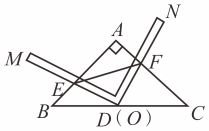 16. 某学校带领名学生到农场参加植树劳动,学校同时租用 , , 三种型号客车去农场,其中 , , 三种型号客车载客量分别为人、人、人,租金分别为元、元、元为了节省资金,学校要求每辆车必须满载,并将学生一次性送到农场植树,请你写出一种满足要求的租车方案 ,满足要求的几种租车方案中,最低租车费用是 元
16. 某学校带领名学生到农场参加植树劳动,学校同时租用 , , 三种型号客车去农场,其中 , , 三种型号客车载客量分别为人、人、人,租金分别为元、元、元为了节省资金,学校要求每辆车必须满载,并将学生一次性送到农场植树,请你写出一种满足要求的租车方案 ,满足要求的几种租车方案中,最低租车费用是 元三、解答题(本大题共12小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算: .18. 解不等式组 .19. 先化简,再求值:已知 , 求的值.20. 如图,在四边形中, , , 为的中点,请你用无刻度的直尺
在图中画的边上的高线小蕊的画法如下请你按照小器的画法完成画图,并填写证明的依据.
画法:
连接 ,
连接 , 交于点 ,
连接 , 交于点 ,
作射线 , 交于点 ,
即为所求的边上的高线
证明:
, 为的中点,
.
,
四边形是平行四边形. ▲ .
点是中点. ▲ .
、是的中线.
是的中线.
,
是边上的高线. ▲ .21. 已知在中, , 点 , 分别是边 , 中点,连接 , , 延长到点 , 使得 , 连接 , . (1)、求证:四边形是菱形;
(1)、求证:四边形是菱形;
(2)、如果 , 且 , 求的长.22. 如图,平面直角坐标系中,一次函数的图象分别与 , 轴交于 , 两点,正比例函数的图象与交于点 .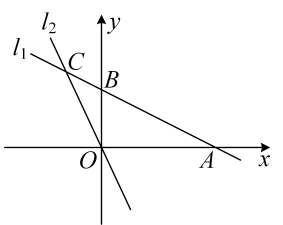 (1)、求的值及的表达式;
(1)、求的值及的表达式;
(2)、一次函数的图象为 , 且 , , 三条直线不能围成三角形,直接写出所有满足条件的的值.23. 北极海冰是地球系统的重要组成部分,其变化可作为全球气候变化的重要指示器为了应对全球气候问题,科学家运用卫星遥感技术对北极海冰覆盖面积的变化情况进行监测,根据对多年的数据进行整理、描述和分析,形成了如下信息:
、年间北极海冰年最低覆盖面积变化的频数分布直方图如下所示:数据分成组: , , , , , , ,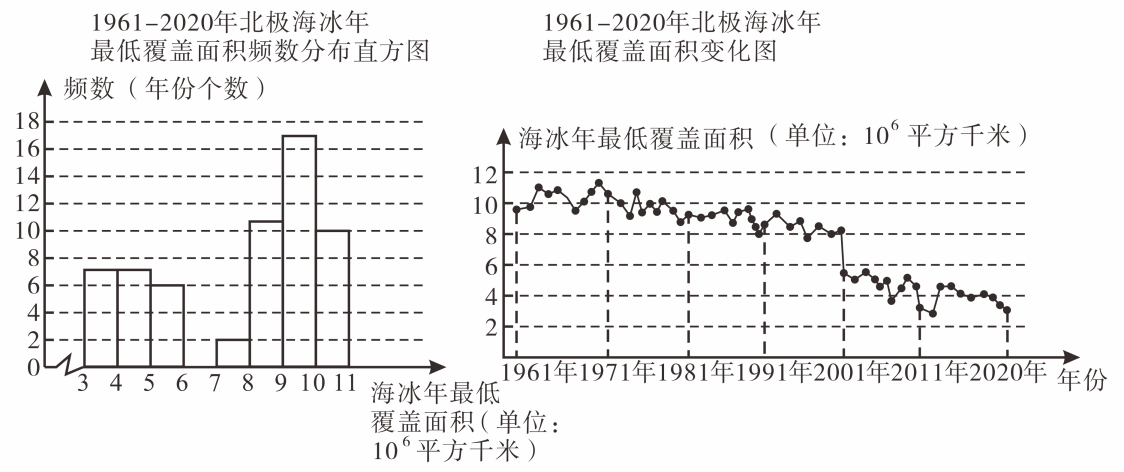
、年间北极海冰年最低覆盖面积的数据在这一组的是: , , , , , , , , , ,(1)、写出年间北极海冰年最低覆盖面积的中位数是 ▲ 平方千米;
(2)、北极海冰最低覆盖面积出现了大面积的缩减是 ▲ 年
(3)、请参考反映年间北极海冰年最低覆盖面积变化的折线图,解决以下问题:
记北极地区年北极海冰年最低覆盖面积的方差为 , 年北极海冰年最低覆盖面积的方差为 , 请直接判断 ▲ 的大小关系填写“”“”或“”;
根据年以后北极海冰年最低覆盖面积的相关数据,推断全球气候发生了怎样的变化?在你的生活中应采取哪些措施应对这一变化?24. 如图,是圆内接三角形,过圆心作 , 连接 , , 过点作 , 交的延长线于点 , .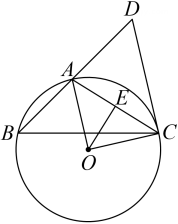 (1)、求证:是的切线;
(1)、求证:是的切线;
(2)、如果 , 求半径的长度.25. 如图,是学校灌溉草坪用到的喷水设备,喷水口离地面垂直高度为米,喷出的水流都可以抽象为平面直角坐标系中的一条抛物线.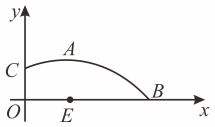 (1)、灌溉设备喷出水流的最远射程可以到达草坪的最外侧边沿点 , 此时,喷水口喷出的水流垂直高度与水平距离的几组数据如下表.
(1)、灌溉设备喷出水流的最远射程可以到达草坪的最外侧边沿点 , 此时,喷水口喷出的水流垂直高度与水平距离的几组数据如下表.水平距离米
竖直高度米
结合数据,求此抛物线的表达式,并求出水流最大射程的长度.
(2)、为了全面灌溉,喷水口可以喷出不同射程的水流,喷水口喷出的另外一条水流形成的抛物线满足表达式 , 此水流最大射程米,求此水流距离地面的最大高度.26. 在平面直角坐标系中,已知点 , 在二次函数的图象上.
(1)、当时,求的值;
(2)、当 , 求的取值范围.27. 直线是线段的垂直平分线,垂足为点 , 点是直线上一点,连接以为斜边作等腰直角 , 连接 .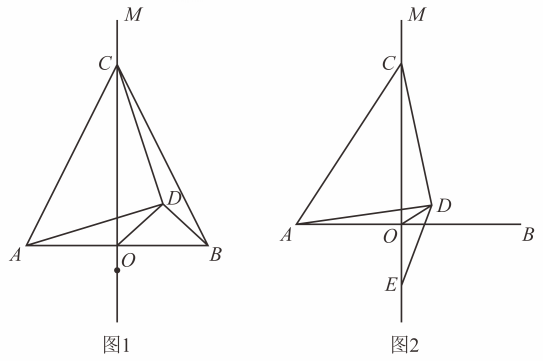 (1)、如图 , 若 , 求的度数;
(1)、如图 , 若 , 求的度数;
(2)、如图所示,点是射线上一点,且 , 连接 , 延长至点 , 使得 , 连接 , 根据题意补全图 , 写出线段 , 之间的关系,并证明.28. 在中, , , 给出如下定义:作直线分别交 , 边于点 , , 点关于直线的对称点为 , 则称为等腰直角关于直线的“直角对称点”点可与点重合,点可与点重合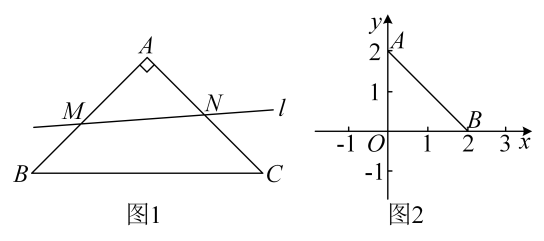 (1)、在平面直角坐标系中,点 , , 直线: , 为等腰直角关于直线的“直角对称点”.
(1)、在平面直角坐标系中,点 , , 直线: , 为等腰直角关于直线的“直角对称点”.
当时,写出点的坐标;
连接 , 求长度的取值范围;(2)、的半径为 , 点是上一点,以点为直角顶点作等腰直角 , 其中 , 直线与、分别交于、两点,同时为等腰直角关于直线的“直角对称点”,连接 , 当点在上运动时,直接写出长度的最大值与最小值.