天津市滨海新区2023年中考二模数学考试试卷

试卷更新日期：2023-10-09 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1. 计算 $3 - (- 3)$ 的结果等于（）

A、 $0$ B、 $6$ C、 $9$ D、 $27$

查看试题解析
2. $2 c o s 45 °$ 的值等于（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $1$ D、 $2$

查看试题解析
3. $2023$ 年第一季度，天津港完成货物吞吐量 $114000000$ 吨，同比增长 $4.71 %$ ，将数字 $114000000$ 用科学记数法表示应为（）

A、 $0.114 \times 1 0^{9}$ B、 $1.14 \times 1 0^{8}$ C、 $11.4 \times 1 0^{7}$ D、 $114 \times 1 0^{6}$

查看试题解析
4. 天津市的旅游形象宣传口号是“天天乐道，津津有味”，下列汉字中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图是一个由 $6$ 个完全相同的正方体组成的立体图形，它的主视图是（）

A、 B、 C、 D、

查看试题解析
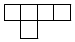6. 估计 $\sqrt{41}$ 的值在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
7. 方程 $x^{2} + 10 x + 9 = 0$ 的两个根是（）

A、 $x_{1} = 1$ ， $x_{2} = 9$ B、 $x_{1} = - 1$ ， $x_{2} = 9$
C、 $x_{1} = 1$ ， $x_{2} = - 9$ D、 $x_{1} = - 1$ ， $x_{2} = - 9$

查看试题解析
8. 计算 $\frac{b + 2}{b + 1} - \frac{1}{b + 1}$ 的结果为（）

A、 $1$ B、 $- 1$ C、 $\frac{1}{b + 1}$ D、 $\frac{2}{b + 1}$

查看试题解析
9. 若点 $A (x_{1} ， - 4)$ ， $B (x_{2} ， 3)$ ， $C (x_{3} ， 6)$ 都在反比例函数 $y = - \frac{10}{x}$ 的图象上，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{3} < x_{2} < x_{1}$ C、 $x_{3} < x_{1} < x_{2}$ D、 $x_{2} < x_{3} < x_{1}$

查看试题解析
10. 如图， $△ A O C$ 是平面直角坐标系中的等腰三角形，顶点 $O$ 的坐标是 $(0 ， 0)$ ，点 $A$ 在第一象限，点 $C$ 在 $x$ 轴的正半轴上 $A O = A C = 5$ ， $O C = 6$ ，则点 $A$ 的坐标是（）

A、 $(3 ， 4)$ B、 $(3 ， 0)$ C、 $(4 ， 3)$ D、 $(0 ， 3)$

查看试题解析
11. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ 是边 $A B$ 上一点，连 $A F$ 接 $D C$ ，将 $△ A D C$ 沿 $D C$ 所在直线折叠得到 $△ F D C$ ，点 $F$ 是点 $A$ 的对应点， $F C$ 与 $A B$ 交于点 $E$ ，下列结论一定正确的是（）

A、 $D C = D B$
B、 $∠ A F C = ∠ D C B$
C、 $C E = C B$
D、 $A D ⊥ D F$

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c$ 大致图象如图所示，其中顶点为 $(2 ， - 9 a)$ ，下列结论 $① a b c > 0$ ； $② 4 a - 2 b + c > 0$ ； $③$ 若方程 $a (x - 5) (x + 1) = - 1$ 有两根为 $x_{1}$ 和 $x_{2}$ ，且 $x_{1} < x_{2}$ ，则 $x_{1} < - 1 < 5 < x_{2}$ ，其中正确的个数是（）

A、 $0$ 个
B、 $1$ 个
C、 $2$ 个
D、 $3$ 个

查看试题解析

二、填空题（本大题共6小题，共18.0分）

13. 计算：a⁵÷a³= ．

查看试题解析
14. 计算 $(\sqrt{15} - 1) (\sqrt{15} + 1)$ 的结果等于．

查看试题解析
15. 不透明的袋子中装有 $10$ 个球，其中有 $3$ 个红球， $7$ 个绿球，这些球除颜色外无其他差别，从袋子中随机取出 $1$ 个球，则它是绿球的概率是．

查看试题解析
16. 将直线 $y = 2 x$ 向上平移1个单位长度，平移后直线的解析式为.

查看试题解析
17. 如图，在矩形 $A B C D$ 中，点 $E$ ， $F$ 分别是较长边 $A D$ ， $B C$ 上的点，且 $E F / / A B$ ， $E D = A B$ ，连接 $O B$ 交 $E F$ 于点 $M$ ，连接 $A M$ ，若 $C F = 2 B F$ ， $A D = 6$ ，则 $A M =$ ．

查看试题解析
18. 如图，在每个小正方形的边长都为 $1$ 的网格中， $△ A B C$ 的顶点 $A$ ， $B$ ， $C$ 都在圆上，点 $A$ ， $B$ 均在格点上，点 $C$ 在网格线上．

(1)、线段 $A B$ 的长为；

(2)、在优弧 $\overset{⏜}{A C B}$ 上找一点 $P$ ，使 $C P = A B$ ，请简要说明点 $P$ 的位置是如何找到的 $($ 不要求证明 $)$ ．

查看试题解析

三、解答题（本大题共7小题，共66.0分。解答应写出文字说明，证明过程或演算步骤）

19. 解不等式组 ${\begin{array}{l} 3 x + 10 \geq 0 ， ① \\ 4 x \leq x + 6 ， ② \end{array}$
请结合题意填空，完成本题的解答
⑴解不等式 $①$ ，得     ▲     ；
⑵解不等式 $②$ ，得     ▲  ；
⑶把不等式 $①$ 和 $②$ 的解集在数轴上表示出来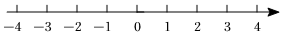

⑷原不等式组的解集为     ▲   ．

查看试题解析
20. 为了解某学校九年级学生开展“综合与实践”活动的情况，抽样调查了该校若干九年级学生上学期参加“综合与实践”活动的天数，并根据调查所得数据绘制了如图所示的统计图 $①$ 和 $②$ ．
根据图中信息，解答下列问题：

(1)、本次接受调查的九年级学生有人，图 $②$ 中 $n$ 的值是；

(2)、求统计的这组学生活动数据的平均数、众数和中位数 $($ 平均数保留一位小数 $)$ ．

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，点 $D$ 是边 $A B$ 上一点，以 $B D$ 为直径的圆 $O$ 与边 $A C$ 相切于点 $E$ ，与边 $B C$ 相交于点 $F$ ， $B F = B O$ ，点 $G$ 是 $B F$ 中点．

(1)、如图 $①$ ，求 $∠ G O B$ 的度数；

(2)、如图 $②$ ，延长 $G O$ 交 $⊙ O$ 于点 $M$ ，连接 $E M$ ，若 $A C = 3 \sqrt{3}$ ， $B F = 2 C F$ ，求 $E M$ 的长．

查看试题解析
22. 如图，某小区内有一个人工湖，小明想知道它的宽度 $.$ 已知他所在的楼正好和人工湖最宽处的 $B$ ， $C$ 两点在一条直线上，他测得 $B$ 处和 $C$ 处的俯角分别是 $67 °$ 和 $22 °$ ，又知小明的观测高度距地面 $20$ 米，此楼和人工湖在同一水平面上，根据上述条件请你计算一下该人工湖最宽处 $B$ ， $C$ 两点间的距离 $($ 结果精确到 $1$ 米 $) .$ 其中 $t a n 67 ° \approx \frac{12}{5}$ ， $t a n 22 ° \approx \frac{2}{5}$ ．

查看试题解析
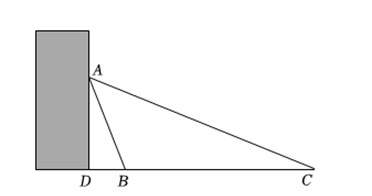23. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．
已知张强家、蔬菜种植基地和农贸市场依次在同一直线上，张强家距蔬菜种植基地 $20$ 公里，张强家距农贸市场 $60$ 公里 $.$ 某天早晨张强从家出发，匀速行驶 $30$ 分钟到达蔬菜种植基地；在基地停留 $40$ 分钟装载蔬菜；然后匀速行驶了 $40$ 分钟到达农贸市场；在农贸市场停留 $60$ 分钟后，匀速行驶 $72$ 分钟返回家中，给出的图象反映了这个过程中张强离开家的距离 $y k m$ 与离开家的时间 $x m i n$ 之间的对应关系．
请根据相关信息，解答下列问题：

(1)、填表：
离开家的时间 $/ m i n$
          $20$
          $40$
          $80$
          $110$
          $200$
离开家的距离 $/ k m$
          $\frac{40}{3}$

          $60$

(2)、填空：
$①$ 蔬菜种植基地与农贸市场的距离是 $k m$ ；
$②$ 从蔬菜种植基地到农贸市场的速度是 $k m / m i n$ ；
$③$ 当张强离家的距离为 $10 k m$ 时，他离开家的时间是 $m i n$ ；

(3)、当 $0 \leq x \leq 110$ 时，请直接写出 $y$ 与 $x$ 的函数解析式．

查看试题解析
24. 如图，在平面直角坐标系中，点 $A$ 在第一象限，点 $B$ 在 $x$ 轴正半轴上， $△ A O B$ 是边长为 $4$ 的等边三角形，点 $C$ ， $D$ 分别在边 $O B$ 和 $A B$ 上， $△ C D B$ 是边长为 $2$ 的等边三角形 $.$ 现将 $△ C D B$ 绕点 $B$ 顺时针旋转，得到 $△ E F B$ ，旋转角为 $α$ ，点 $C$ ， $D$ 的对应点分别是点 $E$ 和 $F$ ．

(1)、如图 $①$ ，连接 $O E$ ，当 $α = 30 °$ 时，求 $O E^{2}$ ；

(2)、如图 $②$ ，连接 $A E$ ， $A F$ ，旋转过程中，当点 $F$ 落到 $x$ 轴 $($ 点 $F$ 在点 $B$ 的右侧 $)$ 时，求 $△ A E F$ 的面积；

(3)、如图 $③$ ，连接 $O E$ ， $A F$ ，若点 $G$ ， $H$ 分别是 $O E$ ， $A F$ 的中点，连接 $B G$ ， $G H$ ， $B H$ ，得 $△ B G H$ ， $△ B G H$ 是什么三角形？请说明理由；若 $△ B G H$ 的面积是 $S$ ，请直接写出 $S$ 的取值范围．

查看试题解析
25. 抛物线 $y = a x^{2} + b x + 4$ 与 $x$ 轴交于 $A$ ， $B$ 两点 $($ 点 $A$ 在点 $B$ 的左侧 $)$ ，与 $y$ 轴交于点 $C$ ，点 $B (3 ， 0)$ ，对称轴为直线 $x = 1$ ．

(1)、求该抛物线的顶点坐标；

(2)、作直线 $B C$ ，点 $P$ 是抛物线上一动点．
$①$ 作直线 $P C$ ，当 $∠ P C B = ∠ A B C$ 时，求点 $P$ 的坐标；
$②$ 当点 $P$ 在第一象限的抛物线上运动时，过点 $P$ 作直线 $B C$ 的垂线交 $B C$ 于点 $E$ ，作 $P F ⊥ y$ 轴交 $B C$ 于点 $F$ ， $P E + P F$ 有最大值吗？若有，请直接写出该值；若没有，请写出理由．

查看试题解析

离开家的时间 $/ m i n$	$20$	$40$	$80$	$110$	$200$
离开家的距离 $/ k m$	$\frac{40}{3}$			$60$