重庆市永川区2023年中考一模数学考试试卷

试卷更新日期：2023-10-09 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1. $- 6$ 的相反数是（）

A、 $6$ B、 $- 6$ C、 $\frac{1}{6}$ D、 $- \frac{1}{6}$

查看试题解析
2. 甲骨文是中国的一种古代文字，是汉字的早期形式.下列甲骨文中，是轴对称图形的是（）.

A、 B、 C、 D、

查看试题解析
3. 将等腰直角三角形纸片和矩形纸片按如图方式叠放在一起，若 $∠ 1 = 30 °$ ，则 $∠ 2$ 的度数为（）

A、 $10 °$ B、 $15 °$ C、 $20 °$ D、 $30 °$

查看试题解析
4. 五一假期，小明去游乐园游玩，坐上了他向往已久的摩天轮．摩天轮上，小明离地面的高度 $h ($ 米 $)$ 和他坐上摩天轮后旋转的时间 $t ($ 分钟 $)$ 之间的部分函数关系如图所示，则下列说法错误的是（）

A、摩天轮旋转一周需要 $6$ 分钟
B、小明出发后的第 $3$ 分钟和第 $9$ 分钟，离地面的高度相同
C、小明离地面的最大高度为 $42$ 米
D、小明出发后经过 $6$ 分钟，离地面的高度为 $3$ 米

查看试题解析
5. 如图， $△ A B C$ 与 $△ D E F$ 是位似图形，点 $O$ 为位似中心，已知 $B O$ ： $O E = 2$ ： $1$ ，则 $△ A B C$ 与 $△ D E F$ 的面积之比是（）

A、 $1$ ： $2$
B、 $1$ ： $4$
C、 $2$ ： $1$
D、 $4$ ： $1$

查看试题解析
6. 用大小相同的圆点摆成如图所示的图案，按照这样的规律摆放，则第 $8$ 个图案中共有圆点的个数是（）

A、 $34$ B、 $40$ C、 $49$ D、 $59$

查看试题解析
7. 估计 $\sqrt{2} (\sqrt{23} - \sqrt{2})$ 的值应在（）

A、 $2$ 和 $3$ 之间 B、 $3$ 和 $4$ 之间 C、 $4$ 和 $5$ 之间 D、 $5$ 和 $6$ 之间．

查看试题解析
8. 一件商品的原价是100元，经过两次提价后的价格为121元，如果每次提价的百分率都是x，根据题意，下面列出的方程正确的是（）

A、 $100 (1 + x) = 121$ B、 $100 (1 - x) = 121$ C、 $100 {(1 + x)}^{2} = 121$ D、 $100 {(1 - x)}^{2} = 121$

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $D$ 是 $A B$ 上的一点，以 $A D$ 为直径的 $⊙ O$ 与 $B C$ 相切于点 $E$ ，连接 $A E$ 、 $D E$ ，若 $∠ B = 30 °$ ， $A C = 3$ ，则 $B D$ 的长度是（）

A、 $\sqrt{3}$ B、 $2$ C、 $3$ D、 $2 \sqrt{3}$

查看试题解析
10. 定义：如果代数式 $A = a_{1} x^{2} + b_{1} x + c_{1} (a_{1} \neq 0 ， a_{1} ， b_{1} ， c_{1}$ 是常数 $)$ 与 $B = a_{2} x^{2} + b_{2} x + c_{2} (a_{2} \neq 0 ， a_{2} ， b_{2} ， c_{2}$ 是常数 $)$ ，满足 $a_{1} + a_{2} = 0$ ， $b_{1} = b_{2}$ ， $c_{1} + c_{2} = 0$ ，则称这两个代数式 $A$ 与 $B$ 互为“同心式”，下列四个结论：
$(1)$ 代数式： $- 3 x^{2} + 2 x$ 的“同心式”为 $3 x^{2} - 2 x$ ；
$(2)$ 若 $8 m x^{2} + n x - 5$ 与 $6 n x^{2} - 4 x + 5$ 互为“同心式”，则 $(m + n)^{2023}$ 的值为 $1$ ；
$(3)$ 当 $b_{1} = b_{2} = 0$ 时，无论 $x$ 取何值时，“同心式” $A$ 与 $B$ 的值始终互为相反数；
$(4)$ 若 $A$ 、 $B$ 互为“同心式”，且 $b_{1}^{2} - 36 a_{1} c_{1} = 0$ ，则 $A - 2 B = 0$ 有两个相等的实数根．
其中，正确的结论有个．（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析

二、填空题（本大题共8小题，共32.0分）

11. 计算： $(3 - π)^{0} + | - \sqrt{3} | =$ ．

查看试题解析
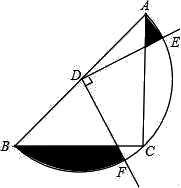
12. 截止 $2022$ 年底，重庆私人汽车拥有量约为 $8200000$ 辆，请把 $8200000$ 用科学记数法表示为．

查看试题解析
13. 已知 $2 x^{| m | - 2} + 3 = 9$ 是关于 $x$ 的一元二次方程，则 $m =$ ．

查看试题解析
14. 盒子里有3张形状、大小、质地完全相同的卡片，上面分别标着数字1，2，3，从中随机抽出1张后不放回，再随机抽出1张，则两次抽出的卡片上的数字之和为奇数的概率是.

查看试题解析
15. 如图，在△ABC中，CA=CB，∠ACB=90°，AB=4，点D为AB的中点，以点D为圆心作圆，半圆恰好经过三角形的直角顶点C，以点D为顶点，作90°的∠EDF，与半圆交于点E，F，则图中阴影部分的面积是．

查看试题解析
16. 如图，正方形 $A B C D$ 中，点 $E$ 、 $F$ 分别在边 $C D$ ， $A D$ 上， $B E$ 与 $C F$ 交于点 $G .$ 若 $B C = 4$ ， $D E = A F = 1$ ，则 $G F$ 的长为．

查看试题解析
17. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} \frac{5 x - 2}{3} \leq x - 2 \\ \frac{a - x}{2} < x + 1 \end{array}$ 无解，且关于 $y$ 的分式方程 $\frac{a y}{y + 1} = \frac{6}{y + 1} - 2$ 的解是整数，则所有满足条件的整数 $a$ 的值之和为．

查看试题解析
18. 若一个多位数右边的数字减去左边相邻的数字的差都是同一个数，我们称这个数为“阶梯数”，其中这个差为阶梯数的阶梯，如三位“阶梯数”有 $123$ ， $135$ ， $147$ ， $159$ ， $258$ ， $753$ ， $852$ ， $\dots$ 等等 $.$ 写出一个阶梯为 $2$ 的四位“阶梯数”为；若一个三位“阶梯数”的各位数字之和大于 $14$ 小于 $18$ ，且阶梯 $a$ 使关于 $x$ 的一元二次方程 $x^{2} - x - (a - 4) = 0$ 有实数解，则这个“阶梯数”为．

查看试题解析

三、解答题（本大题共8小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）

19. 如图，四边形 $A B C D$ 是平行四边形．

(1)、尺规作图 $($ 不写作法，保留作图痕迹 $)$ ：作出 $∠ A B C$ 的角平分线 $B E$ ，交 $A D$ 于点 $E$ ；在线段 $B C$ 上截取 $B F = B A$ ，连接 $E F$ ；

(2)、在 $(1)$ 所作图中，经过学习小组讨论发现四边形 $A B F E$ 是菱形，并给出以下证明，请你补充完整．
证明： $∵$ 四边形 $A B C D$ 为平行四边形，
$∴$       ▲   ；
$∴ ∠ A E B = ∠ C B E$ ．
$∵ B E$ 平分 $∠ A B C$ ，
$∴$      ▲  ．
$∴ ∠ A E B = ∠ A B E$ ．
$∴$       ▲   ．
$∵ A B = B F$ ，
$∴ A E = B F .$ 而 $A E / / B F$ ，
$∴$       ▲  ．
$∵ B A = B F$ ，
$∴$ 四边形 $A B F E$ 为菱形．

查看试题解析
20. 计算：

(1)、 $x (x - 2 y) + (x + y)^{2}$ ；

(2)、 $(2 - \frac{m}{m - 3}) \div \frac{m^{2} - 36}{m^{2} - 6 m + 9}$ ．

查看试题解析

21. 为了解学生掌握垃圾分类知识的情况，增强学生环保意识

.

某学校举行了“垃圾分类人人有责”的知识测试活动，现从该校七、八年级中各随机抽取

20

名学生的测试成绩

(

满分

10

分，

6

分及

6

分以上为合格

)

进行整理、描述和分析，下面给出了部分信息．
七年级

20

名学生的测试成绩为：

7

，

8

，

7

，

9

，

7

，

6

，

5

，

9

，

10

，

9

，

8

，

5

，

8

，

7

，

6

，

7

，

9

，

7

，

10

，

6

．
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、

8

分及以上人数所占百分比如下表所示：

年级	平均数	众数	中位数	$8$ 分及以上人数所占百分比
七年级	$7.5$	$a$	$7$	$45 %$
八年级	$7.5$	$8$	$b$	$C$

根据以上信息，解答下列问题．

(1)、由上表植空

. a =

. b =

. c =

(2)、该校七、八年级共

1200

名学生参加了此次测试活动

.

估计参加此次测试活动成合格的学生数是多少？

(3)、根据上述数据

.

你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好？请说明理由

(

写出一条理由即可

)

查看试题解析

22. 车厘子，其含铁量是水果之首，它营养丰富，深受消费者喜爱 $.$ 某超市准备花 $10000$ 元购进一批车厘子，实际购买时，由于在原进价的基础上打了 $8$ 折，结果用同样的钱比预期多购进了 $100$ 斤．

(1)、车厘子的实际进价为每斤多少元？

(2)、若该品种的车厘子市场售价为 $40$ 元 $/$ 斤，可售出 $200$ 斤，根据销售经验，降低售价会促进销量的增加，即售价每斤降价 $1$ 元，销量相应增加 $20$ 斤，超市决定将部分车厘子降价促销，当售价定为多少元时，可使促销部分的车厘子获利 $4500$ 元？

查看试题解析
23. 我省为实现 $5 G$ 网络全覆盖， $2020 - 2025$ 年拟建设 $5 G$ 基站七千个 $.$ 如图，在坡度为 $i = 1$ ： $2.4$ 的斜坡 $C B$ 上有一建成的基站塔 $A B$ ，小符在坡脚 $C$ 测得塔顶 $A$ 的仰角为 $45 °$ ，然后她沿坡面 $C B$ 行走 $13$ 米到达 $D$ 处，在 $D$ 处测得塔顶 $A$ 的仰角为 $53 ° . ($ 点 $A$ 、 $B$ 、 $C$ 、 $D$ 均在同一平面内 $) ($ 参考数据： $s i n 53 ° \approx \frac{4}{5}$ ， $c o s 53 ° \approx \frac{3}{5}$ ， $t a n 53 ° \approx \frac{4}{3})$

(1)、求 $D$ 处的竖直高度；

(2)、求基站塔 $A B$ 的高．

查看试题解析
24. 一次函数 $y = k x + b (k \neq 0)$ 的图象与反比例函数 $y = \frac{m}{x} (m \neq 0)$ 的图象交于点 $A (a ， 4)$ 和点 $B (- 4 ， - 2)$ ，与 $y$ 轴交于点 $C$ ．

(1)、求反比例函数和一次函数的解析式，并在网格中画出一次函数 $y = k x + b$ 的图象．

(2)、根据图象，直接写出关于 $x$ 的不等式 $k x + b \geq \frac{m}{x}$ 的解集．

(3)、点 $D (4 ， b)$ 在一次函数 $y = k x + b$ 的图象上，过点 $D$ 作 $D F ⊥ y$ 轴于点 $F$ ，交反比例函数的图象于点 $E$ ，连接 $B F$ ， $A E$ ，求四边形 $A B F E$ 的面积．

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 $y = x^{2} + b x + c$ 交 $x$ 轴于 $A (1 ， 0)$ 、 $B$ 两点 $($ 点 $A$ 在点 $B$ 的左侧 $)$ ，交 $y$ 轴于点 $C (0 ， 5)$ ，连接 $B C$ ．

(1)、求该抛物线的解析式；

(2)、如图 $1$ ，将直线 $B C$ 沿 $y$ 轴向上平移 $6$ 个单位长度后与抛物线交于 $D$ 、 $E$ 两点，交 $y$ 轴于点 $G$ ，若点 $P$ 是抛物线上位于直线 $B C$ 下方 $($ 不与 $A$ 、 $B$ 重合 $)$ 的一个动点，过点 $P$ 作 $P M / / y$ 轴交 $D E$ 于点 $M$ ，交 $B C$ 于点 $H$ ，过点 $M$ 作 $M N ⊥ B C$ 于点 $N$ ，求 $P M + N H$ 的最大值及此时点 $P$ 的坐标；

(3)、如图 $2$ ，当点 $P$ 满足 $(2)$ 问条件时，将 $△ C B P$ 绕点 $C$ 逆时针旋转 $α (0 ° < α < 90 °)$ 得到 $△ C B' P'$ ，此时点 $B'$ 恰好落到直线 $E D$ 上，已知点 $F$ 是抛物线上的一个动点，在直线 $E D$ 上是否存在一点 $Q$ ，使得以点 $C$ 、 $B'$ 、 $F$ 、 $Q$ 为顶点的四边形为平行四边形，若存在，请直接写出所有符合条件的点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析
26. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点D为 $B C$ 边上一动点，连接 $A D$ ，将 $A D$ 绕着D点逆时针方向旋转 $90 °$ 得到 $D E$ ，连接 $A E$ .

(1)、如图1， $A H ⊥ B C$ ，点D恰好为 $C H$ 中点， $A E$ 与 $B C$ 交于点G，若 $A B = 4$ ，求 $A E$ 的长度；

(2)、如图2， $D E$ 与 $A B$ 交于点F，连接 $B E$ ，在 $B A$ 延长线上有一点P， $∠ P C A = ∠ E A B$ ，求证： $A B = A P + \sqrt{2} B D$ ；

(3)、如图3， $D E$ 与 $A B$ 交于点F，且 $A B$ 平分 $∠ E A D$ ，点M为线段 $A F$ 上一点，点N为线段 $A D$ 上一点，连接 $D M$ ， $M N$ ，点K为 $D M$ 延长线上一点，将 $△ B D K$ 沿直线 $B K$ 翻折至 $△ B D K$ 所在平面内得到 $△ B Q K$ ，连接 $D Q$ ，在M，N运动过程中，当 $D M + M N$ 取得最小值，且 $∠ D K Q = 4 5^{°}$ 时，请直接写出 $\frac{D Q}{B C}$ 的值.

查看试题解析