甘肃省平凉市2023年中考二模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列设计图中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系中,点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 一元一次不等式组 的解集中,整数解的个数是( )A、4 B、5 C、6 D、75. 如图,数轴上的点 , , , , 分别表示数 , , , , , 则表示数的点应落在( )
3. 在平面直角坐标系中,点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 一元一次不等式组 的解集中,整数解的个数是( )A、4 B、5 C、6 D、75. 如图,数轴上的点 , , , , 分别表示数 , , , , , 则表示数的点应落在( ) A、线段上 B、线段上 C、线段上 D、线段上6. 下列命题是真命题的是( )A、中位数就是一组数据中最中间的一个数
A、线段上 B、线段上 C、线段上 D、线段上6. 下列命题是真命题的是( )A、中位数就是一组数据中最中间的一个数
B、一组数据的众数可以不唯一
C、已知、、是的三条边,则
D、邻边相等的平行四边形是矩形7. 若单项式与是同类项,则 , 的值分别是( )A、 , B、 ,
C、 , D、 ,8. 如图,有一张直角三角形纸片ABC,两条直角边AC=5,BC= 10,将△ABC折叠,使点A和点B重合,折痕为DE,则CD的长为( )
 A、1.8 B、2.5 C、3 D、3.759. 如图,、、是圆上的三点,且四边形是平行四边形,交圆于点 , 则等于( )
A、1.8 B、2.5 C、3 D、3.759. 如图,、、是圆上的三点,且四边形是平行四边形,交圆于点 , 则等于( ) A、
A、
B、
C、
D、10. 在平面直角坐标系中,二次函数的图象如图所示,现给以下结论:
;
;
;
为实数;
.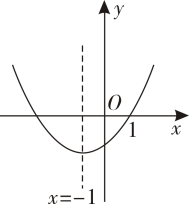
其中错误结论的个数有( )
A、个
B、个
C、个
D、个二、填空题(本大题共8小题,共32.0分)
-
11. .12. 港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一,它是世界总体跨度最长的跨海大桥,全长55000米.数字55000用科学记数法表示为.13. 若是方程的一个根,则的值为 .14. 在一个不透明的盒子中装有除颜色外其他完全相同的若干红球和个白球若每次将球充分搅匀后,任意摸出个球,记下颜色后再放回盒子,通过大量重复试验后,发现摸到白球的频率稳定在左右,则红球的个数约为 .15. 若关于x的一元二次方程 有两个实数根,则k的取值范围是 .16. 如图, , 若 , , , 则 .
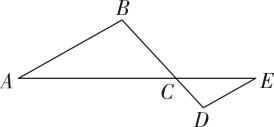 17. 如图,在中, , 以为直径的交于点 , 若 , 则图中阴影部分的面积为 .
17. 如图,在中, , 以为直径的交于点 , 若 , 则图中阴影部分的面积为 . 18. 在公园内,牡丹按正方形形状种植,在它的周围种植芍药,如图反映了牡丹的列数和芍药的数量规律,那么当时,芍药的数量为 株
18. 在公园内,牡丹按正方形形状种植,在它的周围种植芍药,如图反映了牡丹的列数和芍药的数量规律,那么当时,芍药的数量为 株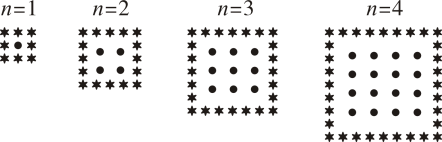
三、计算题
-
19. 解方程: .
四、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
20. 化简: .21. 如图,平分的外角 .
 (1)、尺规作图:作的角平分线 , 交于点保留作图痕迹,不写作法;(2)、若 , 则 .22. 图是一种淋浴喷头,图是图的示意图,若用支架把喷头固定在点处,手柄长 , 与墙壁的夹角 , 喷出的水流与形成的夹角 , 现在住户要求:当人站在处淋浴时,水流正好喷洒在人体的处,且使 , 问:安装师傅应将支架固定在离地面多高的位置?
(1)、尺规作图:作的角平分线 , 交于点保留作图痕迹,不写作法;(2)、若 , 则 .22. 图是一种淋浴喷头,图是图的示意图,若用支架把喷头固定在点处,手柄长 , 与墙壁的夹角 , 喷出的水流与形成的夹角 , 现在住户要求:当人站在处淋浴时,水流正好喷洒在人体的处,且使 , 问:安装师傅应将支架固定在离地面多高的位置?
参考数据: , , , , , , , , .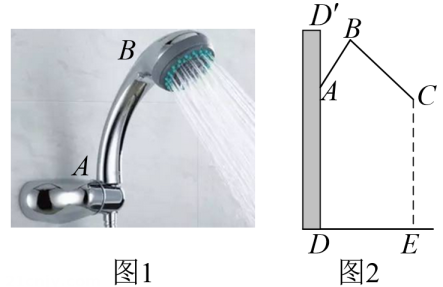 23. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.24. 随着人民生活水平的不断提高,外出旅游已成为家庭生活的一种方式某社区为了解每户家庭旅游的消费情况,随机抽取部分家庭,对每户家庭的年旅游消费金额进行问卷调查,并根据调查结果绘制成如下不完整的统计图表.
23. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.24. 随着人民生活水平的不断提高,外出旅游已成为家庭生活的一种方式某社区为了解每户家庭旅游的消费情况,随机抽取部分家庭,对每户家庭的年旅游消费金额进行问卷调查,并根据调查结果绘制成如下不完整的统计图表.
组别
家庭年旅游消费金额元
户数

请你根据统计图表提供的信息,解答下列问题:
(1)、本次被调查的家庭有 户,表中 .(2)、本次调查数据的中位数落在哪一组?请说明理由.(3)、在扇形统计图中,组所对应扇形的圆心角是多少度?(4)、若该社区有户家庭,请你估计年旅游消费在元以上的家庭户数.25. 如图,一次函数的图象与反比例函数在第一象限的图象交于和两点,与轴交于点 .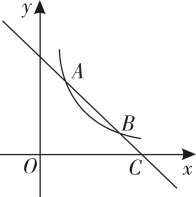 (1)、求反比例函数的解析式;(2)、若点在轴上,且的面积为 , 求点的坐标.26. 如图,在中,弦与弦相交于点 , 于点 , 过点的直线与的延长线相交于点 .
(1)、求反比例函数的解析式;(2)、若点在轴上,且的面积为 , 求点的坐标.26. 如图,在中,弦与弦相交于点 , 于点 , 过点的直线与的延长线相交于点 . (1)、若 , 求证:是的切线.(2)、连接 , 若 , , 求的半径.27.
(1)、若 , 求证:是的切线.(2)、连接 , 若 , , 求的半径.27.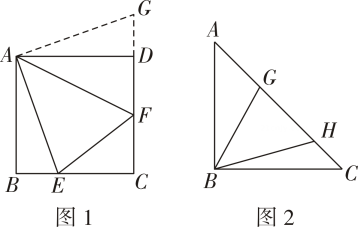 (1)、建立模型:如图 , 在正方形中, , 分别是 , 上的点,且 , 探究图中线段 , , 之间的数量关系小王同学探究此问题的方法是将绕点逆时针旋转使得与重合,连接 , 由此得到 ,再证明≌ ,可得出线段 , , 之间的数量关系为 .(2)、拓展延伸:如图 , 在等腰直角三角形中, , , 点 , 在边上,且 , 写出图中线段 , , 之间的数量关系并证明.28. 如图,在平面直角坐标系中,的边在轴上, , 以为顶点的抛物线经过点 , 交轴于点 , 动点在对称轴上.
(1)、建立模型:如图 , 在正方形中, , 分别是 , 上的点,且 , 探究图中线段 , , 之间的数量关系小王同学探究此问题的方法是将绕点逆时针旋转使得与重合,连接 , 由此得到 ,再证明≌ ,可得出线段 , , 之间的数量关系为 .(2)、拓展延伸:如图 , 在等腰直角三角形中, , , 点 , 在边上,且 , 写出图中线段 , , 之间的数量关系并证明.28. 如图,在平面直角坐标系中,的边在轴上, , 以为顶点的抛物线经过点 , 交轴于点 , 动点在对称轴上.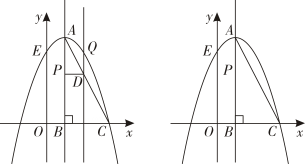 (1)、求抛物线的解析式.(2)、若点从点出发,沿方向以个单位长度秒的速度匀速运动到点停止,设运动时间为秒,过点作交于点 , 过点且平行于轴的直线交抛物线于点 , 连接 , , 当为何值时,的面积最大?最大值是多少?(3)、抛物线上是否存在点 , 使得以点 , , , 为顶点的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式.(2)、若点从点出发,沿方向以个单位长度秒的速度匀速运动到点停止,设运动时间为秒,过点作交于点 , 过点且平行于轴的直线交抛物线于点 , 连接 , , 当为何值时,的面积最大?最大值是多少?(3)、抛物线上是否存在点 , 使得以点 , , , 为顶点的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
-