甘肃省酒泉市2023年中考一模数学考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 中国人最早使用负数,可追溯到两千多年前的秦汉时期,的相反数是( )A、 B、 C、 D、2. 可燃冰是一种新型能源,它的密度很小,可燃冰的质量仅为数字用科学记数法表示是( )A、 B、 C、 D、3. 下列运算中,正确的是( )A、 B、
C、 D、4. 如图,将三角尺直立举起靠近墙面,打开手机手电筒照射三角尺,在墙面上形成影子.则三角尺与影子之间属于以下哪种图形变换( )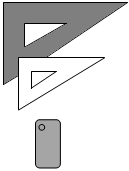 A、平移 B、轴对称 C、旋转 D、位似5. 如图,在数轴上标注了四段范围,则表示的点落在( )
A、平移 B、轴对称 C、旋转 D、位似5. 如图,在数轴上标注了四段范围,则表示的点落在( ) A、第 段 B、第 段 C、第 段 D、第 段6. 在某县中小学安全知识竞赛中,参加决赛的6个同学获得的分数分别为(单位:分):95、97、97、96、98、99,对于这6个同学的成绩下列说法正确的是( )A、众数为95 B、极差为3 C、平均数为96 D、中位数为977. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A、第 段 B、第 段 C、第 段 D、第 段6. 在某县中小学安全知识竞赛中,参加决赛的6个同学获得的分数分别为(单位:分):95、97、97、96、98、99,对于这6个同学的成绩下列说法正确的是( )A、众数为95 B、极差为3 C、平均数为96 D、中位数为977. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )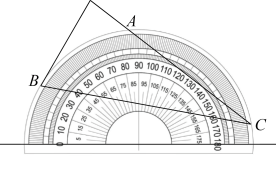 A、28° B、30° C、36° D、56°8. 如图,在中, , , , 以点为圆心,长为半径画弧,与交于点 , 再分别以、为圆心,大于的长为半径画弧,两弧交于点、 , 作直线 , 分别交、于点、 , 则的长度为( )
A、28° B、30° C、36° D、56°8. 如图,在中, , , , 以点为圆心,长为半径画弧,与交于点 , 再分别以、为圆心,大于的长为半径画弧,两弧交于点、 , 作直线 , 分别交、于点、 , 则的长度为( ) A、
A、
B、
C、
D、9. 中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有个,甜果有个,则可列方程组为( )A、 B、 C、 D、10. 如图 , 在平行四边形中,点沿方向从点移动到点 , 设点移动路程为 , 线段的长为 , 图是点运动时随变化的关系图象,则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
11. 分解因式: =.12. 一副三角板如图摆放,直线 , 则的度数是 .
 13. 老师为帮助学生正确理解物理变化与化学变化,将种生活现象制成看上去无差别的卡片如图从中随机抽取一张卡片,抽中生活现象是物理变化的概率是 .
13. 老师为帮助学生正确理解物理变化与化学变化,将种生活现象制成看上去无差别的卡片如图从中随机抽取一张卡片,抽中生活现象是物理变化的概率是 . 14. 如图,在中,边的垂直平分线交于点 , 连接 , 若 , , 则的周长是 .
14. 如图,在中,边的垂直平分线交于点 , 连接 , 若 , , 则的周长是 . 15. 若 , 则以、为边长的等腰三角形的周长为 .16. 如图是第四套人民币角硬币,该硬币边缘镌刻的正多边形的外角的度数为
15. 若 , 则以、为边长的等腰三角形的周长为 .16. 如图是第四套人民币角硬币,该硬币边缘镌刻的正多边形的外角的度数为 17. 已知关于的一元二次方程有实数根,则的取值范围是 .18. 如图,在直角坐标系中,△ABC的顶点C与原点O重合,点A在反比例函数y= (k>0,x>0)的图象上,点B的坐标为(4,3),AB与y轴平行,若AB=BC,则k= .
17. 已知关于的一元二次方程有实数根,则的取值范围是 .18. 如图,在直角坐标系中,△ABC的顶点C与原点O重合,点A在反比例函数y= (k>0,x>0)的图象上,点B的坐标为(4,3),AB与y轴平行,若AB=BC,则k= .
三、计算题(本大题共1小题,共4.0分)
-
19. 计算: .
四、解答题(本大题共9小题,共62.0分。解答应写出文字说明,证明过程或演算步骤)
-
20. 先化简,再求值: ,其中 .21. 如图,四边形中, , , 于点 .
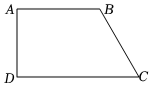 (1)、用尺规作的角平分线,交于点;不写作法,保留作图痕迹(2)、连接求证:四边形是菱形.22. 为传承酒泉文明、弘扬民族精神某校“综合与实践”小组开展了测量鼓楼如图高度的实践活动,请你帮他们完成下面的实践报告,测量鼓楼高度的实践报告:
(1)、用尺规作的角平分线,交于点;不写作法,保留作图痕迹(2)、连接求证:四边形是菱形.22. 为传承酒泉文明、弘扬民族精神某校“综合与实践”小组开展了测量鼓楼如图高度的实践活动,请你帮他们完成下面的实践报告,测量鼓楼高度的实践报告:活动课题
测量鼓楼高度
活动目的
运用三角函数知识解决实际问题
活动工具
测角仪、皮尺等测量工具
方案示意图

测量步骤
如图
利用测角仪站在处测得城门楼最高点的仰角为;
前进了米到达处选择测点 , 与在同一水平线上, , 两点之间的距离可直接测得,测角仪高度忽略不计 , 在处测得点的仰角为 .参考数据
, , , , , .
计算鼓楼的高度结果保留整数
23. 已知甲袋中有个红球,个白球,乙袋中有个红球,个白球,从甲、乙两袋中各摸出个球,摸出的两个球都是红球的概率是多少?琪琪给出了下面的解题过程,请判断琪琪的解题过程是否正确,如不正确,请写出正确的解题过程琪琪的解法:用树状图列出所有可能的结果如图所示;从树状图可以看出一共有种等可能的结果,其中两个球都是红球的结果有种,所以摸出的两个球都是红球的概率为 .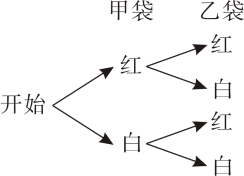 24. 为了了解学生在一年中的课外阅读量,九班对九年级名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:本以下;本;本;本以上根据调查结果统计整理并制作了如图所示的两幅统计图表:
24. 为了了解学生在一年中的课外阅读量,九班对九年级名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:本以下;本;本;本以上根据调查结果统计整理并制作了如图所示的两幅统计图表:各种情况人数统计频数分布表 课外阅读情况 A B C D 频数 20 x y 40  (1)、表中 , 的值分别为: , ;(2)、在扇形统计图中,部分所对应的扇形的圆心角是 度;(3)、根据抽样调查结果,请估计九年级学生一年阅读课外书本以上的学生人数.25. 如图,一次函数的图象与反比例函数的图象相交于点点 .
(1)、表中 , 的值分别为: , ;(2)、在扇形统计图中,部分所对应的扇形的圆心角是 度;(3)、根据抽样调查结果,请估计九年级学生一年阅读课外书本以上的学生人数.25. 如图,一次函数的图象与反比例函数的图象相交于点点 . (1)、求此一次函数和反比例函数的表达式;(2)、如图所示,请直接写出不等式的解集;(3)、 在轴上存在一点 , 使的周长最小,求点P的坐标.26. 如图,AB是的直径,AC是的弦,AD平分∠CAB交于点D,过点D作的切线EF,交AB的延长线于点E,交AC的延长线于点F.
(1)、求此一次函数和反比例函数的表达式;(2)、如图所示,请直接写出不等式的解集;(3)、 在轴上存在一点 , 使的周长最小,求点P的坐标.26. 如图,AB是的直径,AC是的弦,AD平分∠CAB交于点D,过点D作的切线EF,交AB的延长线于点E,交AC的延长线于点F. (1)、求证:;(2)、若 , , , 求BE的长.27.
(1)、求证:;(2)、若 , , , 求BE的长.27.
 (1)、感知:如图 , 四边形和均为正方形,与的数量关系为 ;(2)、拓展:如图 , 四边形和均为菱形,且 , 请判断与的数量关系,并说明理由;(3)、应用:如图 , 四边形和均为菱形,点在边上,点在延长线上若 , , 的面积为 , 求菱形的面积.28. 跳台滑雪是冬季奥运会的比赛项目.如图,运动员通过助滑道后在点处腾空,在空中沿抛物线飞行,直至落在着陆坡上的点处.腾空点到地面的距离为 , 坡高为 , 着陆坡的坡度即为:以为原点,所在直线为轴,所在直线为轴,建立如图所示的平面直角坐标系.已知这段抛物线经过点 , .
(1)、感知:如图 , 四边形和均为正方形,与的数量关系为 ;(2)、拓展:如图 , 四边形和均为菱形,且 , 请判断与的数量关系,并说明理由;(3)、应用:如图 , 四边形和均为菱形,点在边上,点在延长线上若 , , 的面积为 , 求菱形的面积.28. 跳台滑雪是冬季奥运会的比赛项目.如图,运动员通过助滑道后在点处腾空,在空中沿抛物线飞行,直至落在着陆坡上的点处.腾空点到地面的距离为 , 坡高为 , 着陆坡的坡度即为:以为原点,所在直线为轴,所在直线为轴,建立如图所示的平面直角坐标系.已知这段抛物线经过点 , . (1)、求这段抛物线表示的二次函数表达式;(2)、在空中飞行过程中,求运动员到坡面竖直方向上的最大距离;(3)、落点与坡顶之间的距离为
(1)、求这段抛物线表示的二次函数表达式;(2)、在空中飞行过程中,求运动员到坡面竖直方向上的最大距离;(3)、落点与坡顶之间的距离为
-