北京市海淀区2023年中考一模考试试卷
试卷更新日期:2023-10-09 类型:中考模拟
一、选择题(本大题共8小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列几何体中,主视图为如图的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 北京植物园从上世纪五十年代开始建设种子库,目前库中已有种子余份,总量位居世界第二位将用科学记数法表示应为( )A、 B、 C、 D、3. 在一条沿直线铺设的电缆两侧有甲、乙两个小区,现要求在上选取一点 , 向两个小区铺设电缆下面四种铺设方案中,使用电缆材料最少的是( )A、
2. 北京植物园从上世纪五十年代开始建设种子库,目前库中已有种子余份,总量位居世界第二位将用科学记数法表示应为( )A、 B、 C、 D、3. 在一条沿直线铺设的电缆两侧有甲、乙两个小区,现要求在上选取一点 , 向两个小区铺设电缆下面四种铺设方案中,使用电缆材料最少的是( )A、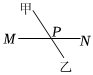 B、
B、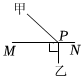 C、
C、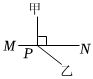 D、
D、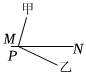 4. 不透明的袋子中装有个红球和个黄球,两种球除颜色外无其他差别,从中随机摸出一个小球,摸到黄球的概率是( )A、 B、 C、 D、5. 实数m,n在数轴上的对应点的位置如图所示,下列结论中正确的是( )
4. 不透明的袋子中装有个红球和个黄球,两种球除颜色外无其他差别,从中随机摸出一个小球,摸到黄球的概率是( )A、 B、 C、 D、5. 实数m,n在数轴上的对应点的位置如图所示,下列结论中正确的是( )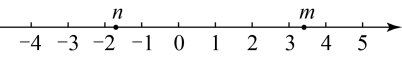 A、 B、 C、 D、6. 若关于的一元二次方程有两个相等的实数根,则的值是( )A、 B、 C、 D、7. 小明制作简易工具来测量物体表面的倾斜程度,方法如下:将刻度重新设计的量角器固定在等腰直角三角板上,使量角器的刻度线与三角板的底边平行将用细线和铅锤做成的重锤线顶端固定在量角器中心点处,现将三角板底边紧贴被测物体表面,如图所示,此时重锤线在量角器上对应的刻度为 , 那么被测物体表面的倾斜角为( )
A、 B、 C、 D、6. 若关于的一元二次方程有两个相等的实数根,则的值是( )A、 B、 C、 D、7. 小明制作简易工具来测量物体表面的倾斜程度,方法如下:将刻度重新设计的量角器固定在等腰直角三角板上,使量角器的刻度线与三角板的底边平行将用细线和铅锤做成的重锤线顶端固定在量角器中心点处,现将三角板底边紧贴被测物体表面,如图所示,此时重锤线在量角器上对应的刻度为 , 那么被测物体表面的倾斜角为( ) A、 B、 C、 D、8. 图是变量与变量的函数关系的图象,图是变量与变量的函数关系的图象,则与的函数关系的图象可能是( )
A、 B、 C、 D、8. 图是变量与变量的函数关系的图象,图是变量与变量的函数关系的图象,则与的函数关系的图象可能是( )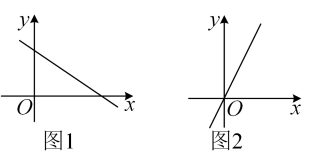 A、
A、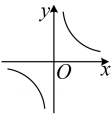 B、
B、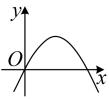 C、
C、 D、
D、
二、填空题(本大题共8小题,共16.0分)
-
9. 若 在实数范围内有意义,则实数x的取值范围是 .10. 分解因式:a2b+4ab+4b= .11. 分式方程的解为 .12. 根据如表估计 精确到 .13. 如图,菱形的对角线交于点 , 点为的中点,连接若 , , 则的长为 .
 14. 在平面直角坐标系中,反比例函数的图象与正比例函数的图象交于 , 两点,点的坐标为 , 则点的坐标为 .15. 如图,点在正六边形的边上运动若 , 写出一个符合条件的的值 .
14. 在平面直角坐标系中,反比例函数的图象与正比例函数的图象交于 , 两点,点的坐标为 , 则点的坐标为 .15. 如图,点在正六边形的边上运动若 , 写出一个符合条件的的值 . 16. 某陶艺工坊有和两款电热窑,可以烧制不同尺寸的陶艺品,两款电热窑每次可同时放置陶艺品的尺寸和数量如表所示.
16. 某陶艺工坊有和两款电热窑,可以烧制不同尺寸的陶艺品,两款电热窑每次可同时放置陶艺品的尺寸和数量如表所示.尺寸
数量个
款式大
中
小
烧制一个大尺寸陶艺品的位置可替换为烧制两个中尺寸或六个小尺寸陶艺品,但烧制较小陶艺品的位置不能替换为烧制较大陶艺品.
某批次需要生产个大尺寸陶艺品,个中尺寸陶艺品,个小尺寸陶艺品.(1)、烧制这批陶艺品,款电热窑至少使用 次;(2)、若款电热窑每次烧制成本为元,款电热窑每次烧制成本为元,则烧制这批陶艺品成本最低为 元三、解答题(本大题共12小题,共68.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算: .18. 解不等式组: .19. 已知 , 求代数式的值.20. 下面是小明同学证明定理时使用的两种添加辅助线的方法,选择其中一种,完成证明.
定理:在直角三角形中,如果一个锐角等于 , 那么它所对的直角边等于斜边的一半.
已知:如图,在中, , .
求证: .
方法一
证明:如图,延长到点 , 使得 , 连接 .
方法二
证明:如图,在线段上取一点 , 使得 , 连接 . 21. 如图,在四边形中, , 过点作交于点 , 点为边上一点, , 连接 .
21. 如图,在四边形中, , 过点作交于点 , 点为边上一点, , 连接 . (1)、求证:四边形为矩形;(2)、若 , , , 求的长.22. 在平面直角坐标系中,一次函数的图象过点 , .(1)、求这个一次函数的解析式;(2)、当时,对于的每一个值,一次函数的值大于一次函数的值,直接写出的取值范围.23. 如图,为的直径,为上一点,为的中点,交的延长线于点 .
(1)、求证:四边形为矩形;(2)、若 , , , 求的长.22. 在平面直角坐标系中,一次函数的图象过点 , .(1)、求这个一次函数的解析式;(2)、当时,对于的每一个值,一次函数的值大于一次函数的值,直接写出的取值范围.23. 如图,为的直径,为上一点,为的中点,交的延长线于点 . (1)、求证:直线为的切线;(2)、延长 , 交于点若 , , 求的长.24. 某小组对当地年月至月西红柿与黄瓜市场价格进行调研,经过整理、描述和分析得到了部分信息.
(1)、求证:直线为的切线;(2)、延长 , 交于点若 , , 求的长.24. 某小组对当地年月至月西红柿与黄瓜市场价格进行调研,经过整理、描述和分析得到了部分信息.
西红柿与黄瓜市场价格的折线图:

西红柿与黄瓜价格的众数和中位数:蔬菜价格
众数
中位数
西红柿元千克
黄瓜元千克
根据以上信息,回答下列问题:
(1)、 , ;(2)、在西红柿与黄瓜中, 的价格相对更稳定;(3)、如果这两种蔬菜的价格随产量的增大而降低,结合题中信息推测这两种蔬菜在 月的产量相对更高.25. “兔飞猛进”谐音成语“突飞猛进”在自然界中,野兔善于奔跑跳跃,“兔飞猛进”名副其实野兔跳跃时的空中运动路线可以看作是抛物线的一部分.(1)、建立如图所示的平面直角坐标系.
通过对某只野兔一次跳跃中水平距离单位:与竖直高度单位:进行的测量,得到以下数据:
水平距离
竖直高度
根据上述数据,回答下列问题:
野兔本次跳跃的最远水平距离为 , 最大竖直高度为 ;
求满足条件的抛物线的解析式;(2)、已知野兔在高速奔跑时,某次跳跃的最远水平距离为 , 最大竖直高度为若在野兔起跳点前方处有高为的篱笆,则野兔此次跳跃 填“能”或“不能”跃过篱笆.26. 在平面直角坐标系中,点 , 在抛物线上.(1)、当 , 时,比较与的大小,并说明理由;(2)、若对于 , 都有 , 求的取值范围.
