北京市朝阳区2023年中考一模数学考试试卷

试卷更新日期：2023-10-09 类型：中考模拟

进入出卷网下载

一、选择题（本大题共8小题，共16.0分。在每小题列出的选项中，选出符合题目的一项）

1. 如图是某几何体的三视图，该几何体是（）

A、长方体
B、圆锥
C、三棱柱
D、圆柱

查看试题解析
2. 我国已建成世界上规模最大的社会保障体系、医疗卫生体系，基本养老保险覆盖 $1040000000$ 人左右，将 $1040000000$ 用科学记数法表示应为（）

A、 $1.04 \times 1 0^{10}$ B、 $1.04 \times 1 0^{9}$ C、 $10.4 \times 1 0^{9}$ D、 $0.104 \times 1 0^{11}$

查看试题解析
3. 如图，若数轴上的点 $A$ 表示下列四个无理数中的一个，则这个无理数是（）

A、 $- \sqrt{2}$ B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $π$

查看试题解析
4. 如图，直线 $A B$ ， $C D$ 相交于点O，若 $∠ A O C = 60 °$ ， $∠ B O E = 40 °$ ，则 $∠ D O E$ 的度数为（）

A、 $60 °$ B、 $40 °$ C、 $20 °$ D、 $10 °$

查看试题解析
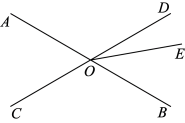5. 经过某路口的汽车，只能直行或右转 $.$ 若这两种可能性大小相同，则经过该路口的两辆汽车都直行的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
6. 正六边形的外角和是（）

A、 $720 °$ B、 $540 °$ C、 $360 °$ D、 $180 °$

查看试题解析
7. 某中学为了解学生对四类劳动课程的喜欢情况，从本校学生中随机抽取了 $200$ 名进行问卷调查，根据数据绘制了如图所示的统计图 $.$ 若该校有 $2000$ 名学生，估计喜欢木工的人数为（）

A、 $64$ B、 $380$ C、 $640$ D、 $720$

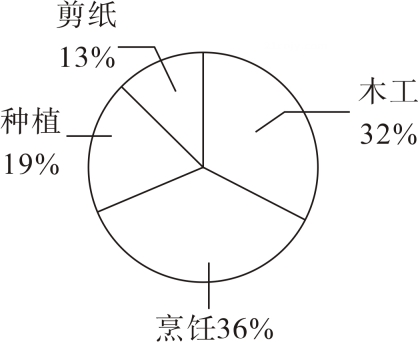查看试题解析
8. 下面的三个问题中都有两个变量：
$①$ 矩形的面积一定，一边长 $y$ 与它的邻边长 $x$ ；
$②$ 某村的耕地面积一定，人均耕地面积 $S$ 与全村总人口 $n$ ；
$③$ 汽车的行驶速度一定，行驶路程 $s$ 与行驶时间 $t$ ．
其中，两个变量之间的函数关系可以用形如 $y = \frac{k}{x} (k$ 为常数， $k \neq 0)$ 的式子表示的是（）

A、 $① ②$ B、 $① ③$ C、 $② ③$ D、 $① ② ③$

查看试题解析

二、填空题（本大题共8小题，共16.0分）

9. 若 $\sqrt{x - 5}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
10. 分解因式： $3 a^{2} - 6 a + 3 =$ ．

查看试题解析
11. 关于x的一元二次方程x²+6x+m=0有两个相等的实数根，则m的值为.

查看试题解析
12. 方程 $\frac{3}{x + 2} = \frac{2}{x}$ 的解为．

查看试题解析
13. 在平面直角坐标系 $x O y$ 中，若反比例函数 $y = \frac{6}{x}$ 的图象经过点 $A (2 ， m)$ 和点 $B (- 2 ， n)$ ，则 $m + n =$ ．

查看试题解析
14. 如图，在 $△ A B C$ 中， $D E$ 是 $A C$ 的垂直平分线， $A C = 6 .$ 若 $△ A B D$ 的周长为 $13$ ，则 $△ A B C$ 的周长为．

查看试题解析
15. 如图，在矩形 $A B C D$ 中，点 $E$ 在 $A D$ 边上，连接 $B E$ 并延长，交 $C D$ 的延长线于点 $F .$ 若 $A B = 2$ ， $B C = 4$ ， $\frac{A E}{D E} = 2$ ，则 $B F$ 的长为．

查看试题解析
16. 一个 $33$ 人的旅游团到一家酒店住宿，酒店的客房只剩下 $4$ 间一人间和若干间三人间，住宿价格是一人间每晚 $100$ 元，三人间每晚 $130$ 元 $. ($ 说明：男士只能与男士同住，女士只能与女士同住，三人间客房可以不住满，但每间每晚仍需支付 $130$ 元 $.)$

(1)、若该旅游团一晚的住宿房费为 $1530$ 元，则他们租住了间一人间；

(2)、若该旅游团租住了 $3$ 间一人间，且共有 $19$ 名男士，则租住一晚的住宿房费最少为元 $.$

查看试题解析

三、解答题（本大题共12小题，共68.0分。解答应写出文字说明，证明过程或演算步骤）

17. 计算： $(π - \sqrt{3})^{0} - 2 s i n 45 ° + | - \sqrt{2} | + \sqrt{8}$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} x + 1 > 7 - 2 x \\ x \leq \frac{4 + 2 x}{3} \end{array}$ ．

查看试题解析
19. 已知 $x^{2} - x - 3 = 0$ ，求代数式 $(x + 2) (x - 2) - x (2 - x)$ 的值．

查看试题解析
20. 下面是证明“等腰三角形的两个底角相等”的两种添加辅助线的方法，选择其中一种，完成证明．
已知：如图，在 $△ A B C$ 中， $A B = A C .$ 求证： $∠ B = ∠ C$ ．
方法一
证明：如图，作 $△ A B C$ 的中线 $A D$ ．
方法二
证明：如图，作 $△ A B C$ 的角平分线 $A D$ ．

查看试题解析
21. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ，点 $E$ ， $F$ 在 $B D$ 上， $A E / / C F$ ，连接 $A F$ ， $C E$ ．

(1)、求证：四边形 $A E C F$ 为平行四边形；

(2)、若 $∠ E A O + ∠ C F D = 180 °$ ，求证：四边形 $A E C F$ 是矩形．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $(0 ， 1)$ ， $(- 2 ， 2)$ ，与 $x$ 轴交于点 $A$ ．

(1)、求该一次函数的表达式及点 $A$ 的坐标；

(2)、当 $x \geq 2$ 时，对于 $x$ 的每一个值，函数 $y = 2 x + m$ 的值大于一次函数 $y = k x + b (k \neq 0)$ 的值，直接写出 $m$ 的取值范围．

查看试题解析
23. 如图， $A B$ 是 $⊙ O$ 的弦，过点 $O$ 作 $O C ⊥ A B$ ，垂足为 $C$ ，过点 $A$ 作 $⊙ O$ 的切线，交 $O C$ 的延长线于点 $D$ ，连接 $O B$ ．

(1)、求证： $∠ B = ∠ D$ ；

(2)、延长 $B O$ 交 $⊙ O$ 于点 $E$ ，连接 $A E$ ， $C E$ ，若 $A D = 2 \sqrt{5}$ ， $s i n B = \frac{\sqrt{5}}{5}$ ，求 $C E$ 的长．

查看试题解析
24. 某校为了解读书月期间学生平均每天阅读时间，在该校七、八、九年级学生中各随机抽取了 $15$ 名学生，获得了他们平均每天阅读时间 $($ 单位： $m i n)$ ，并对数据进行了整理、描述，给出部分信息．
$a .$ 七、八年级学生平均每天阅读时间统计图：

$b .$ 九年级学生平均每天阅读时间：
$21 ㅤ 22 ㅤ 25 ㅤ 33 ㅤ 36 ㅤ 36 ㅤ 37 ㅤ 37 ㅤ 39 ㅤ 39 ㅤ 41 ㅤ 42 ㅤ 46 ㅤ 48 ㅤ 50$
$c .$ 七、八、九年级学生平均每天阅读时间的平均数：
年级
七
八
九
平均数
          $26.4$
          $35.2$
          $36.8$
根据以上信息，回答下列问题：

(1)、抽取的 $15$ 名九年级学生平均每天阅读时间的中位数是；

(2)、求三个年级抽取的 $45$ 名学生平均每天阅读时间的平均数；

(3)、若七、八、九年级抽取的学生平均每天阅读时间的方差分别为 $s_{1}^{2}$ ， $s_{2}^{2}$ ， $s_{3}^{2}$ ，则 $s_{1}^{2}$ ， $s_{2}^{2}$ ， $s_{3}^{2}$ 之间的大小关系为．

查看试题解析

25. 一位滑雪者从某山坡滑下并滑完全程，滑行距离

s (

单位：

m)

与滑行时间

t (

单位：

s)

近似满足“一次函数”、“二次函数”或“反比例函数”关系中的一种

.

测得一些数据如下：

滑行时间 $t / s$	$0$	$1$	$2$	$3$	$4$
滑行距离 $s / m$	$0$	$2$	$6$	$12$	$20$

(1)、

s

是

t

的函数

(

填“一次”、“二次”或“反比例”

)

；

(2)、求

s

关于

t

的函数表达式；

(3)、已知第二位滑雪者也从该山坡滑下并滑完全程，且滑行距离与第一位滑雪者相同，滑行距离

s (

单位：

m)

与滑行时间

t (

单位：

s)

近似满足函数关系

s = \frac{5}{2} t^{2} + 2 t .

记第一位滑雪者滑完全程所用时间为

t_{1}

，第二位滑雪者滑完全程所用时间为

t_{2}

，则

t_{1}

t_{2} (

填“

<

”，“

=

”或“

>

”

)

．

查看试题解析

26. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + (2 m - 6) x + 1$ 经过点 $(1 ， 2 m - 4)$ ．

(1)、求 $a$ 的值；

(2)、求抛物线的对称轴 $($ 用含 $m$ 的式子表示 $)$ ；

(3)、点 $(- m ， y_{1})$ ， $(m ， y_{2})$ ， $(m + 2 ， y_{3})$ 在抛物线上，若 $y_{2} < y_{3} \leq y_{1}$ ，求 $m$ 的取值范围．

查看试题解析
27. 如图， $∠ M O N = α$ ，点 $A$ 在 $O N$ 上，过点 $A$ 作 $O M$ 的平行线，与 $∠ M O N$ 的平分线交于点 $B$ ，点 $C$ 在线段 $O B$ 上 $($ 不与点 $O$ ， $B$ 重合 $)$ ，连接 $A C$ ，将线段 $A C$ 绕点 $A$ 顺时针旋转 $180 ° - α$ ，得到线段 $A D$ ，连接 $B D$ ．

(1)、直接写出线段 $A O$ 与 $A B$ 之间的数量关系，并证明 $∠ M O B = ∠ D B A$ ；

(2)、连接 $D C$ 并延长，分别交 $A B$ ， $O M$ 于点 $E$ ， $F .$ 若 $α = 60 °$ ，用等式表示线段 $E F$ 与 $A C$ 之间的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，对于点 $P$ ， $C$ ， $Q ($ 点 $P$ 与点 $C$ 不重合 $)$ ，给出如下定义：若 $∠ P C Q = 90 °$ ，且 $\frac{C Q}{C P} = \frac{1}{k}$ ，则称点 $Q$ 为点 $P$ 关于点 $C$ 的“ $k -$ 关联点”．
已知点 $A (3 ， 0)$ ，点 $B (0 ， 3 \sqrt{3})$ ， $⊙ O$ 的半径为 $r$ ．

(1)、 $①$ 在点 $D (0 ， 3)$ ， $E (0 ， - 1.5)$ ， $F (3 ， 3)$ 中，是点 $A$ 关于点 $O$ 的“ $1 -$ 关联点”的为；
$②$ 点 $B$ 关于点 $O$ 的“ $\sqrt{3} -$ 关联点”的坐标为；

(2)、点 $P$ 为线段 $A B$ 上的任意一点，点 $C$ 为线段 $O B$ 上任意一点 $($ 不与点 $B$ 重合 $)$ ．
$①$ 若 $⊙ O$ 上存在点 $P$ 关于点 $O$ 的“ $\sqrt{3} -$ 关联点”，直接写出 $r$ 的最大值及最小值；
$②$ 当 $r = 3 \sqrt{21}$ 时， $⊙ O$ 上不存在点 $P$ 关于点 $C$ 的“ $k -$ 关联点”，直接写出 $k$ 的取值范围：．

查看试题解析

已知：如图，在 $△ A B C$ 中， $A B = A C .$ 求证： $∠ B = ∠ C$ ．
方法一证明：如图，作 $△ A B C$ 的中线 $A D$ ．	方法二证明：如图，作 $△ A B C$ 的角平分线 $A D$ ．

年级	七	八	九
平均数	$26.4$	$35.2$	$36.8$