【备考2024】2023年高考数学新高考Ⅱ卷真题变式分层精准练:第5题
试卷更新日期:2023-10-08 类型:二轮复习
一、原题
-
1. 已知椭圆C:的左,右焦点分别为 , , 直线y=x+m与C交于点A,B两点,若面积是 的 2 倍, 则m=( )A、 B、 C、 D、
二、基础
-
2. 已知椭圆E:的右焦点为 , 左顶点为 , 若E上的点P满足轴, , 则E的离心率为( )A、 B、 C、 D、3. 已知分别是椭圆的左,右焦点,M,N是椭圆上两点,且 , 则椭圆的离心率为( )A、 B、 C、 D、4. 已知椭圆的右焦点为 , 过原点的直线与交于两点,若 , 且 , 则的离心率为( )A、 B、 C、 D、5. 已知椭圆的左,右两焦点为和 , P为椭圆上一点,且 , 则( )A、8 B、12 C、16 D、646. 若双曲线的两条渐近线与椭圆:的四个交点及椭圆的两个焦点恰为一个正六边形的顶点,则椭圆的离心率为( )A、 B、 C、 D、7. 已知 , 为椭圆的左、右焦点,过原点O且倾斜角为30°的直线l与椭圆C的一个交点为A,若 , , 则椭圆C的方程为( )A、 B、 C、 D、8. 已知椭圆的下焦点为 , 右顶点为 , 直线交椭圆于另一点 , 且 , 则椭圆的离心率是( )A、 B、 C、 D、9. 如图,是椭圆的左、右顶点,是上不同于的动点,线段与椭圆交于点 , 若 , 则椭圆的离心率为( )
 A、 B、 C、 D、10. 已知直线与抛物线交于A,B两点,线段AB的中点为M,O为坐标原点,直线OM与抛物线C交于O,N,若 , 则p=( )A、 B、1 C、2 D、411. 已知椭圆的右焦点为 , 上顶点为 , 若直线与圆:相切,则该椭圆的离心率为( )A、 B、 C、 D、或12. 已知椭圆的左,右焦点分别为 , , 为椭圆上一点, , 点到直线的距离为 , 则椭圆的离心率为( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知直线与抛物线交于A,B两点,线段AB的中点为M,O为坐标原点,直线OM与抛物线C交于O,N,若 , 则p=( )A、 B、1 C、2 D、411. 已知椭圆的右焦点为 , 上顶点为 , 若直线与圆:相切,则该椭圆的离心率为( )A、 B、 C、 D、或12. 已知椭圆的左,右焦点分别为 , , 为椭圆上一点, , 点到直线的距离为 , 则椭圆的离心率为( )A、 B、 C、 D、三、提升
-
13. 已知椭圆:的左、右焦点分别为、 , 以为圆心的圆与轴交于 , 两点,与轴正半轴交于点 , 线段与交于点.若与的焦距的比值为 , 则的离心率为( )A、 B、 C、 D、14. 点为椭圆的右顶点,为椭圆上一点(不与重合),若(是坐标原点),则椭圆的离心率的取值范围是( )A、 B、 C、 D、15. 设椭圆的左右焦点分别为 , , 是椭圆上不与顶点重合的一点,记为的内心.直线交轴于点, , 且 , 则椭圆的离心率为( )A、 B、 C、 D、16. 设椭圆的左右焦点分别为 , , 是椭圆上不与顶点重合的一点,记是的内心直线交轴于点, , 且 , 则椭圆的离心率为
 ( ) A、 B、 C、 D、17. 已知、为椭圆与双曲线的公共焦点,P是其一个公共点, , 则椭圆与双曲线离心率之积的最小值为( )A、 B、1 C、 D、218. 设椭圆C:的左、右焦点分别为 , , 直线l过点.若点关于l的对称点P恰好在椭圆C上,且 , 则C的离心率为( )A、 B、 C、 D、19. 设为椭圆的两个焦点,点在上,若 , 则( )A、1 B、2 C、4 D、520. 已知双曲线C:的左、右焦点为 , , 过的直线l分别交双曲线C的左、右两支于A、B.若 , 则双曲线C的渐近线方程为( )A、 B、 C、 D、21. 如图, , 分别为椭圆的左、右焦点,点在椭圆上,是面积为的正三角形,则的值是( )
( ) A、 B、 C、 D、17. 已知、为椭圆与双曲线的公共焦点,P是其一个公共点, , 则椭圆与双曲线离心率之积的最小值为( )A、 B、1 C、 D、218. 设椭圆C:的左、右焦点分别为 , , 直线l过点.若点关于l的对称点P恰好在椭圆C上,且 , 则C的离心率为( )A、 B、 C、 D、19. 设为椭圆的两个焦点,点在上,若 , 则( )A、1 B、2 C、4 D、520. 已知双曲线C:的左、右焦点为 , , 过的直线l分别交双曲线C的左、右两支于A、B.若 , 则双曲线C的渐近线方程为( )A、 B、 C、 D、21. 如图, , 分别为椭圆的左、右焦点,点在椭圆上,是面积为的正三角形,则的值是( ) A、 B、 C、 D、22. 已知点是椭圆上一点,椭圆的左、右焦点分别为、 , 且 , 则的面积为( )A、6 B、12 C、 D、23. 已知F为抛物线的焦点,过F的直线与抛物线C交于A,B两点,与圆交于D,E两点,A,D在y轴的同侧,则( )A、1 B、4 C、8 D、16
A、 B、 C、 D、22. 已知点是椭圆上一点,椭圆的左、右焦点分别为、 , 且 , 则的面积为( )A、6 B、12 C、 D、23. 已知F为抛物线的焦点,过F的直线与抛物线C交于A,B两点,与圆交于D,E两点,A,D在y轴的同侧,则( )A、1 B、4 C、8 D、16四、培优
-
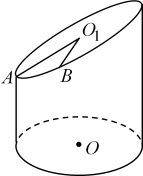
24. 已知圆与圆交点的轨迹为 , 过平面内的点作轨迹的两条互相垂直的切线,则点的轨迹方程为( )A、 B、 C、 D、25. 点均在抛物线上,若直线分别经过两定点 , 则经过定点 , 直线分别交轴于 , 为原点,记 , 则的最小值为( )A、 B、 C、 D、26. 一底面半径为1的圆柱,被一个与底面成45°角的平面所截(如图),为底面圆的中心,为截面的中心,为截面上距离底面最小的点,到圆柱底面的距离为1,为截面图形弧上的一点,且 , 则点到底面的距离是( )
 A、 B、 C、 D、27. 已知抛物线的顶点为坐标原点 , 焦点在轴上,过点的直线交于两点,且 , 线段的中点为 , 则直线的斜率的最大值为( )A、 B、 C、 D、1
A、 B、 C、 D、27. 已知抛物线的顶点为坐标原点 , 焦点在轴上,过点的直线交于两点,且 , 线段的中点为 , 则直线的斜率的最大值为( )A、 B、 C、 D、1
-