【备考2024】2023年高考数学新高考Ⅱ卷真题变式分层精准练：第3题
试卷更新日期：2023-10-08 类型：二轮复习
一、原题
-
1. 某学校为了了解学生参加体育运动的情况，用比例分配的分层随机抽样法作抽样调查，拟从初中部和高中部两层共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同抽样结果共有（ ）.A、种 B、种 C、种 D、 种
二、基础
-
2. 为丰富同学们的暑假生活，暑假期间学校给同学们安排了6场线上讲座，其中讲座只能安排在第一或最后一场，讲座和必须相邻，问不同的安排方法共有（ ）A、144种 B、96种 C、56种 D、34种3. 对图中的A、B、C、D四个区域染色，每块区域染一种颜色，有公共边的区域不同色，
A
B
C
D
现有红、黄、蓝三种不同颜色可以选择，则不同的染色方法共有（ ）
A、12种 B、18种 C、20 D、22种4. 要排出某班一天中语文、数学、政治、英语、体育、艺术6堂课的课程表，要求数学排在上午（前4节），体育课排在下午（后2节），不同排法种数是（ ）A、720 B、192 C、180 D、1445. 为提高学生的身体素质，某校开设了游泳和篮球课程，甲、乙、丙3位同学每人从中任选1门课程参加，则不同的选法共有（ ）A、5种 B、6种 C、8种 D、9种6. 广东省新高考采用的是“”模式：“3”为全国统考科目语文､数学､外语，所有学生必考；“1”为首选科目，考生须在物理､历史科目中选择1个科目；“2”为再选科目，考生可在思想政治､地理､化学､生物4个科目中选择2个科目.已知小明同学必选化学，那么他可选择的方案共有（ ）A、4种 B、6种 C、8种 D、12种7. 保家卫国是每个公民应尽的义务，是一种神圣的职责，捍卫国家安全是每个公民的使命．防止外敌入侵，是中国军人的最高责任、最神圣的任务和最明确的目标，为增强学生爱国意识，激发学生爱国热情，某校组织学生进行爱国观影活动，备选影片有《建军大业》《我的1919》《湄公河行动》《空天猎》《厉害了我的国》5部，若甲、乙、丙三位同学每人只能选择观看其中一部影片，则不同的选择结果共有（ ）A、10种 B、27种 C、60种 D、125种8. 某校为了丰富课后服务活动，提高学校办学水平和教育质量，开设近20门选修课供学生自愿选择.甲、乙2名同学都对其中的合唱、足球、篮球、机器人课程感兴趣，若这2名同学从这4门课程中各自任选一门课程参加，则不同的选法有（ ）A、4种 B、6种 C、8种 D、16种9. 春节期间，某地政府在该地的一个广场布置了一个如图所示的圆形花坛，花坛分为5个区域．现有5种不同的花卉可供选择，要求相邻区域不能布置相同的花卉，且每个区域只布置一种花卉，则不同的布置方案有（ ）
A、120种 B、240种 C、420种 D、720种10. 共有10级台阶，某人一步可跨一级台阶，也可跨两级台阶或三级台阶，则他恰好6步上完台阶的方法种数是（ ）A、30 B、90 C、75 D、6011. 为了贯彻落实中央新疆工作座谈会和全国对口支援新疆工作会议精神，促进边疆少数民族地区教育事业发展，我市教育系统选派了6名教师支援新疆4个不同的地区，要求A，B两个地区各安排一人，剩下两个地区各安排两人，则不同的分派方法有（ ）A、90种 B、180种 C、270种 D、360种三、提升
-
12. 将5名教育志愿者分配到甲、乙、丙和丁4个学校进行支教，每名志愿者只分配到1个学校，每个学校至少分配1名志愿者，则不同的分配方案共有（ ）A、60种 B、120种 C、240种 D、480种13. 年月日是中国共产党成立周年，习近平总书记代表党和人民庄严宣告，经过全党全国各族人民持续奋斗，我们实现了第一个百年奋斗目标，在中华大地上全面建成了小康社会，历史性地解决了绝对贫困问题．某数学兴趣小组把三个、两个、两个与一个组成一个八位数如 ， 若其中三个均不相邻，则这个八位数的个数为（ ）A、 B、 C、 D、14. 用种不同颜色给图中的、、、四个区域涂色，规定一个区域只涂一种颜色，相邻的区域颜色不同，共有种不同的涂色方案．（ ）
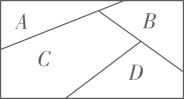A、 B、 C、 D、15. 2022年11月30日，神舟十四号宇航员陈冬、刘洋、蔡旭哲和神舟十五号宇航员费俊龙、邓清明、张陆顺利“会师太空”，为记录这一历史时刻，他们准备在天和核心舱合影留念.假设6人站成一排，要求神舟十四号三名航天员互不相邻，且神舟十五号三名航天员也互不相邻，则他们的不同站法共有（ ）种A、72 B、144 C、36 D、10816. 随着杭州亚运会的临近，吉祥物“琮琮、莲莲、宸宸”开始走俏国内外.现有个完全相同的“宸宸”，甲、乙、丙位体育爱好者要与这个“宸宸”站成一排拍照留念，则有且只有个“宸宸”相邻的排队方法数为（ ）A、36 B、48 C、72 D、14417. 如图，在两行三列的网格中放入标有数字的六张卡片，每格只放一张卡片，则“只有中间一列两个数字之和为5”的不同的排法有（ ）
A、96种 B、64种 C、32种 D、16种18. 将英文单词“”中的6个字母重新排列，其中字母b不相邻的排列方法共有（ ）A、120种 B、240种 C、480种 D、960种19. 今年中国空间站将进入到另一个全新的正式建造阶段，首批参加中国空间站建造的6名航天员，将会分别搭乘着神舟十四号和神舟十五号载人飞船，接连去往中国空间站，并且在上面“会师”中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱．假设中国空间站要安排甲，乙，丙，丁等6名航天员开展实验，其中天和核心舱安排3人，问天实验舱安排2人，梦天实验的安排1人．若甲、乙两人不能同时在一个舱内做实验，则不同的安排方案共有（ ）A、44种 B、48种 C、60种 D、50种20. 某旅游景区有如图所示A至H共8个停车位，现有2辆不同的白色车和2辆不同的黑色车，要求相同颜色的车不停在同一行也不停在同一列，则不同的停车方法总数为（ ）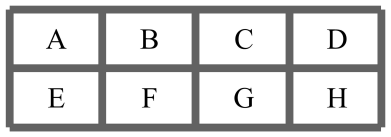
A、288 B、336 C、576 D、168021. 重庆九宫格火锅，是重庆火锅独特的烹饪方式．九宫格下面是相通的，实现了“底同火不同，汤通油不通”它把火锅分为三个层次，不同的格子代表不同的温度和不同的牛油浓度，其锅具抽象成数学形状如图（同一类格子形状相同）：“中间格“火力旺盛，不宜久煮，适合放一些质地嫩脆、顷刻即熟的食物；
“十字格”火力稍弱，但火力均匀，适合煮食，长时间加热以锁住食材原香；
“四角格”属文火，火力温和，适合焖菜，让食物软糯入味．现有6种不同食物（足够量），其中1种适合放入中间格，3种适合放入十字格，2种适合放入四角格．现将九宫格全部放入食物，且每格只放一种，若同时可以吃到这六种食物（不考虑位置），则有多少种不同放法（ ）
A、108 B、36 C、9 D、6四、培优
-
22. 数学对于一个国家的发展至关正要，发达国家常常把保持数学领先地位作为他们的战略需求.现某大学为提高数学系学生的数学素养，特开设了“古今数学思想”，“世界数学通史”，“儿何原本”，“什么是数学”四门选修课程，要求数学系每位同学每学年至多选3门，大一到大三三学年必须将四门选修课程选完，则每位同学的不同选修方式在（ ）A、60种 B、78种 C、84种 D、144种23. 某厂安排名工人到三个岗位值班，每名工人只去一个岗位，每个岗位至少安排名工人，则安排工人甲､乙到同一个岗位值班的方法数为（ ）A、24 B、36 C、60 D、9024. 一堆苹果中大果与小果的比例为 ， 现用一台水果分选机进行筛选．已知这台分选机把大果筛选为小果的概率为 ， 把小果筛选为大果的概率为 ． 经过一轮筛选后，现在从这台分选机筛选出来的“大果”里面随机抽取一个，则这个“大果”是真的大果的概率为（ ）A、 B、 C、 D、25. 某校大一新生A，B，C，D欲加入该校的文学社、书法社、羽毛球社．已知这4名大一新生每人只加入了1个社团，则这4名大一新生恰好加入其中2个社团的不同情况有（ ）A、21种 B、30种 C、42种 D、60种26. 小小的火柴棒可以拼成几何图形，也可以拼成数字.如下图所示，我们可以用火柴棒拼出1至9这9个数字比如：“1”需要2根火柴棒，“7”需要3根火柴棒.若用8根火柴棒以适当的方式全部放入右面的表格中
（没有放入火柴棒的空位表示数字“0”），那么最多可以表示无重复数字的三位数的个数为（ ）.
A、8 B、12 C、16 D、2027. 2021年4月15日，是第六个全民国家安全教育日，教育厅组织宣讲团到某市的六个不同高校进行国家安全知识的宣讲，时间顺序要求是：高校甲必须排在第二或第三个，且高校甲宣讲结束后需立即到高校丁宣讲，高校乙､高校丙的宣讲顺序不能相邻，则不同的宣讲顺序共有（ ）A、28种 B、32种 C、36种 D、44种28. 2020年11月，中国国际进口博览会在上海举行，本次进博会设置了“云采访”区域，通过视频连线，帮助中外记者采访因疫情影响无法来沪参加进博会的跨国企业CEO或海外负责人．某新闻机构安排4名记者和3名摄影师对本次进博会进行采访，其中2名记者和1名摄影师负责“云采访”区域的采访，另2名记者和2名摄影师分两组（每组记者和摄影师各1人），分别负责“汽车展区”和“技术装备展区”的现场采访．如果所有记者、摄影师都能承担三个采访区域的相应工作，则所有不同的安排方案有（ ）A、36种 B、48种 C、72种 D、144种
-
