湖北省武汉市江汉区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-10-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数是无理数的是（）

A、 $\frac{1}{3}$ B、0 C、 $- \frac{1}{2}$ D、 $π$

查看试题解析
2. 下列调查中，适合进行全面调查的是（）

A、调查全国中学生视力情况 B、调查某批次导弹的杀伤半径 C、调查某校七年级1班全体同学期末考试数学成绩 D、调查某批次手电筒的使用寿命

查看试题解析
3. 不等式组 ${\begin{array}{l} x > 1 \\ x > 2 \end{array}$ 的解集是（）

A、x＞2 B、x＞1 C、1＜x＜2 D、无解

查看试题解析
4. 下列各组x，y的值，不是方程 $2 x + y = 16$ 的解的是（）

A、 ${\begin{array}{l} x = 4 \\ y = 8 \end{array}$ B、 ${\begin{array}{l} x = 6 \\ y = 4 \end{array}$ C、 ${\begin{array}{l} x = 10 \\ y = - 4 \end{array}$ D、 ${\begin{array}{l} x = - 2 \\ y = 12 \end{array}$

查看试题解析
5. 已知点 $M (3 ， 4)$ ，若直线 $M N$ 与x轴平行，则N点坐标可能是（）

A、 $(3 ， 5)$ B、 $(4 ， 5)$ C、 $(5 ， 3)$ D、 $(5 ， 4)$

查看试题解析
6. 如图，若 $A B ∥ C D$ ， $B E ⊥ D E$ ， $∠ B = 42 °$ ，则 $∠ D$ 的度数为（）

A、 $42 °$ B、 $48 °$ C、 $52 °$ D、 $58 °$

查看试题解析
7. 一个样本容量为 $80$ 的样本，最大值是 $118$ ，最小值是 $77$ ，取组距为 $4$ ，则可以分成（）

A、 $21$ 组 B、 $20$ 组 C、 $11$ 组 D、 $10$ 组

查看试题解析
8. 下列计算正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $\sqrt{0.4} = 0.2$ C、 $\sqrt{{(- 2)}^{2}} = - 2$ D、 $\sqrt[3]{{(- 2)}^{3}} = - 2$

查看试题解析
9. 七年级1班学生参加运土劳动，一部分学生抬土，另一部分学生挑土，已知全班共用箩筐60个，扁担36根，求抬土、挑土的学生各多少人？如果设抬土的学生x人，挑土的学生y人，则可得方程组（）

A、 ${\begin{array}{l} \frac{x}{2} + 2 y = 60 \\ \frac{x}{2} + y = 36 \end{array}$ B、 ${\begin{array}{l} \frac{x}{2} + 2 y = 60 \\ 2 x + y = 36 \end{array}$ C、 ${\begin{array}{l} 2 x + 2 y = 60 \\ \frac{x}{2} + y = 36 \end{array}$ D、 ${\begin{array}{l} x + 2 y = 60 \\ 2 x + y = 36 \end{array}$

查看试题解析
10. 若 $a > b$ ，则下列不等式一定成立的是（）

A、 $a c^{2} > b c^{2}$ B、 $2 a > b$ C、 $1 - a < 2 - b$ D、 $\frac{1}{a} < \frac{1}{b}$

查看试题解析

二、填空题

11. 16的算术平方根是

查看试题解析
12. 把方程 $x - y = 5$ 改写成用含x的式子表示y的形式为．

查看试题解析
13. 若点 $P (m - 1 ， 2 m + 4)$ 在x轴上，则 $m =$ ．

查看试题解析
14. 已知不等式组 ${\begin{array}{l} x - 1 < a \\ x + 2 b > 1 \end{array}$ 的解集是 $- 1 < x < 3$ ，则 $a + b$ 的值是．

查看试题解析
15. 已知方程组 ${\begin{array}{l} x + 2 y = 4 k \\ 2 x + y = 6 - k \end{array}$ ，若 $x + y = 2023$ ，则 $k =$ ．

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ，将 $△ A B C$ 沿 $A B$ 方向平移得到 $△ D E F$ ， $E F = 8$ ， $B E = 3$ ， $C B$ 与 $D F$ 交于点G， $C G = 4$ ，则图中阴影部分的面积为．

查看试题解析

三、解答题

17.

(1)、计算： $| \sqrt{2} - 2 | + \sqrt{4} - \sqrt[3]{64}$ ；

(2)、解方程组： ${\begin{array}{l} 2 x + y = 5 \\ 3 x - 2 y = 4 \end{array}$ ．

查看试题解析
18. 求不等式组 ${\begin{array}{l} 2 (x - 1) + 3 x \leq 8 ① \\ \frac{x - 2}{2} + 1 < \frac{2 x}{3} ② \end{array}$ 的整数解，可按下列步骤完成解答：

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来：

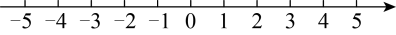(4)、原不等式组的解集为：；

(5)、所以不等式组的整数解为：．

查看试题解析

19. 某校七年级全体学生进行数学计算竞赛，随机抽取部分学生测试成绩进行统计，得到如下的统计表和统计图：

组别	分数范围（x）
A	$50 < x \leq 60$
B	$60 < x \leq 70$
C	$70 < x \leq 80$
D	$80 < x \leq 90$
E	$90 < x \leq 100$

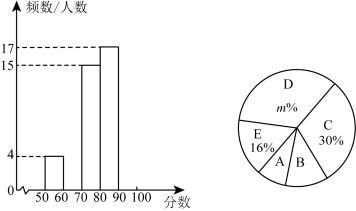(1)、共抽取名学生测试成绩，扇形统计图中

m =

；

(2)、补全频数分布直方图；

(3)、如果该校七年级一共800名学生，规定考试80（含）以上为优秀，请你估计该校七年级大约有多少名同学本次计算竞赛成绩优秀？

查看试题解析

20. 如图， $∠ B C D = ∠ B F E$ ， $∠ 1 + ∠ 2 = 180 °$ ．

(1)、求证： $A D ∥ C E$ ；

(2)、若 $D A ⊥ A B$ ， $∠ 1 - ∠ 2 = 80 °$ ，求 $∠ B E F$ 的度数．

查看试题解析
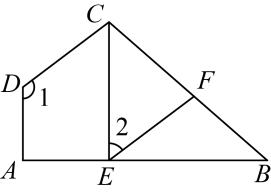21. 如图，网格中每个小正方形的边长为1个单位长度，每个小正方形的顶点称为格点，已知图中A，B，C三点都是格点．

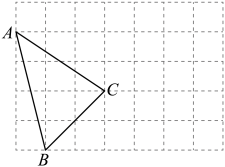(1)、若在坐标平面中 $A (- 2 ， 3)$ ， $C (1 ， 1)$ ，则点B的坐标为；

(2)、将 $△ A B C$ 先向上平移一个单位，再向右平移4个单位，得到 $△ A_{1} B_{1} C_{1}$ ，在网格中画出 $△ A_{1} B_{1} C_{1}$ （A与 $A_{1}$ 对应，B与 $B_{1}$ 对应）；

(3)、直接写出线段 $A C$ 在两次平移中一共扫过的面积为；

(4)、在射线 $B C$ 上标出点E，使 $∠ B E B_{1} = ∠ A B C$ ，得到的三角形 $A B E$ 的面积为 ▲ ．

查看试题解析

四、填空题

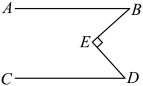
22. 甲、乙、丙三人到超市购零食，甲买薯片3包、饼干2袋、糖果1盒，花费24元；乙买薯片1包、饼干4袋、糖果2盒，花费23元，那么丙买薯片4包，花费元．

查看试题解析
23. 小明在4张同样的纸片上各写了一个正整数，从中随机抽取2张，并将上面的数相加，反复这样做，每次所得的和都只是6，7，8，9中的一个数，并且这4个数都能得到．这4张纸片上的数分别是．

查看试题解析
24. 如图， $∠ A E C = 80 °$ ，在 $∠ A E C$ 的两边上分别过点A和点C向同方向作射线 $A B$ 和 $C D$ ，且 $A B ∥ C D$ ，若 $∠ E A B$ 和 $∠ E C D$ 的角平分线所在的直线交于点P（P与C不重合），则 $∠ A P C$ 的大小为．

查看试题解析
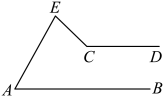25. 对于三个数 $a$ ， $b$ ， $c$ ，规定 $m i n {a ， b ， c}$ 表示这三个数中最小的数， $m a x {a ， b ， c}$ 表示这三个数中最大的数．例如： $m i n {- 1 ， 2 ， 3} = - 1$ ， $m a x {- 1 ， 2 ， 3} = 3$ ．若 $m i n {5 ， 5 - 2 x ， 2 x + 5} = m a x {2 ， x + 1 ， 2 x}$ ，则 $x$ 的值为．

查看试题解析

五、解答题

26. 某校七年级组织学生外出进行研学活动，现有 $40$ 座和 $45$ 座两种客车可供租用，若租 $m$ 辆 $40$ 座车，需要花费 $2000$ 元租车费用，但有 $15$ 人没有座位；若租 $m$ 辆 $45$ 座车，则需要花费 $2200$ 元租车费用，但最后一辆车人数超过 $5$ 人，不足 $15$ 人．

(1)、求 $m$ 的值和出行人数；

(2)、学校准备一共租 $m$ 辆车，若预算租车费用不超过 $2110$ 元，且保证所有人都有座位可坐，一共有哪几种租车方案？

(3)、在（2）的条件下，直接写出最少租车费用．

查看试题解析
27. 定义运算： $f (x ， y) = a x + b y$ ，已知 $f (2 ， 3) = 7$ ， $f (3 ， 4) = 10$ ．

(1)、直接写出： $a =$ ， $b =$ ；

(2)、若关于 $x$ 的不等式组 ${\begin{array}{l} f (x + 1 ， 2 - x) \geq 0 \\ f (2 x ， x - t) < 0 \end{array}$ 无解，求 $t$ 的取值范围；

(3)、若 $f (m x + 3 n ， 2 m - n x) \geq 3 m + 4 n$ 的解集为 $x \leq \frac{1}{3}$ ，求不等式 $f (m x - m ， 3 n - n x) \geq m + n$ 的解集．

查看试题解析
28. 已知点 $A (a ， 0)$ ，点 $B (0 ， b)$ ，且a、b满足 $\sqrt{2 a - b - 6} + {(a - 2 b)}^{2} = 0$ ．

(1)、直接写出点A，B的坐标；

(2)、已知点 $P (m ， n)$ 满足 $2 m + n = 0$ ，且三角形 $P A B$ 面积为5（即 $S_{△ P A B} = 5$ ），求点P坐标；

(3)、点 $M (x ， y)$ 为线段 $A B$ 上一点．
①求 $x + 2 y$ 的值；

②若 $Q (4 ， 4)$ ，三角形 $M O Q$ 面积为S，若关于 $t$ 的不等式 $t \leq S$ 有4个正整数解，请直接写出x的取值范围．

查看试题解析