人教版初中数学2023-2024学年八年级上学期第一次月考试卷(第11章、第12章)
试卷更新日期:2023-10-08 类型:月考试卷
一、选择题
-
1. 下列四个图形中,属于全等图形的是( )
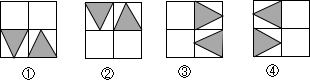 A、①和② B、②和③ C、①和③ D、③和④2. 以下四种作边上的高,其中正确的作法是( )A、
A、①和② B、②和③ C、①和③ D、③和④2. 以下四种作边上的高,其中正确的作法是( )A、 B、
B、 C、
C、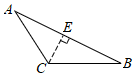 D、
D、 3. 将直角三角板和直尺按照如图位置摆放,若 , 则的度数是( ).
3. 将直角三角板和直尺按照如图位置摆放,若 , 则的度数是( ). A、 B、 C、 D、4. 如图,直线 , 则( )
A、 B、 C、 D、4. 如图,直线 , 则( )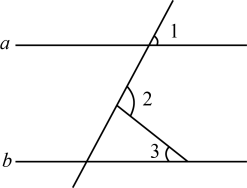 A、 B、 C、 D、5. 一个多边形的内角和是外角和的3倍,则这个多边形的边数( )A、9 B、8 C、7 D、66. 如图,平分 , 、、分别是射线、射线、射线上的点,、、与点都不重合,连接、若添加下列条件中的某一个,就能使≌你认为要添加的那个条件是( )
A、 B、 C、 D、5. 一个多边形的内角和是外角和的3倍,则这个多边形的边数( )A、9 B、8 C、7 D、66. 如图,平分 , 、、分别是射线、射线、射线上的点,、、与点都不重合,连接、若添加下列条件中的某一个,就能使≌你认为要添加的那个条件是( )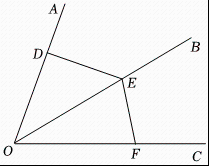 A、 B、 C、 D、7. 如图, , , 平分 , 则的大小为( )
A、 B、 C、 D、7. 如图, , , 平分 , 则的大小为( ) A、 B、 C、 D、8. 下列所给条件中,能画出唯一的的是( )A、 B、 C、 D、9. 一个多边形截取一个角后,形成另一个多边形的内角和是1620,则原来多边形的边数是( )A、10 B、11 C、12 D、以上都有可能10. 如图:①②③中,∠A=42°,∠1=∠2,∠3=∠4,则( )度.
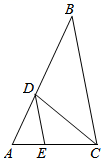
A、 B、 C、 D、8. 下列所给条件中,能画出唯一的的是( )A、 B、 C、 D、9. 一个多边形截取一个角后,形成另一个多边形的内角和是1620,则原来多边形的边数是( )A、10 B、11 C、12 D、以上都有可能10. 如图:①②③中,∠A=42°,∠1=∠2,∠3=∠4,则( )度. A、84 B、111 C、225 D、20111. 如图,BD是△ABC的中线,点E为BD上一点,BE=2ED , 连接AE并延长,交BC于点F , 若△ABC的面积是24cm2 , 则△AED的面积是( )
A、84 B、111 C、225 D、20111. 如图,BD是△ABC的中线,点E为BD上一点,BE=2ED , 连接AE并延长,交BC于点F , 若△ABC的面积是24cm2 , 则△AED的面积是( ) A、2cm2 B、3cm2 C、4cm2 D、6cm212. 如图, , BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若 , 则点P到BC的距离是( )
A、2cm2 B、3cm2 C、4cm2 D、6cm212. 如图, , BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若 , 则点P到BC的距离是( ) A、10 B、8 C、5 D、2
A、10 B、8 C、5 D、2二、填空题
-
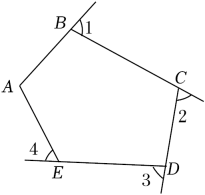
13. 如图,五边形ABCDE的一个内角∠A=110°,则∠1+∠2+∠3+∠4等于 .
 14. 三个全等三角形摆成如图所示的形式,则的度数为.
14. 三个全等三角形摆成如图所示的形式,则的度数为. 15. 如图,平分 , , , 垂足分别为 , , , , 则 .
15. 如图,平分 , , , 垂足分别为 , , , , 则 . 16. 如图,于于 , 且点从向运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发运分钟后,与全等.
16. 如图,于于 , 且点从向运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发运分钟后,与全等. 17. 如图,是的角平分线, , 垂足为 , 连结 . 若 , , 则的度数为 .
17. 如图,是的角平分线, , 垂足为 , 连结 . 若 , , 则的度数为 .
三、计算题