江苏省苏州市2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-10-08 类型:期末考试
一、单选题
-
1. 如果一个三角形的两边长分别为2和4,则第三边长可能是( )A、8 B、6 C、4 D、22. 下列运算不正确的是( )A、 B、 C、 D、3. 不等式组 的解集在数轴上可以表示为( )。A、
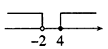 B、
B、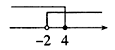 C、
C、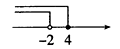 D、
D、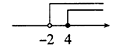 4. 把代数式分解因式,下列结果中正确的是A、 B、 C、 D、5. 下列四个图形中,线段BE是△ABC的高的是( )A、
4. 把代数式分解因式,下列结果中正确的是A、 B、 C、 D、5. 下列四个图形中,线段BE是△ABC的高的是( )A、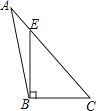 B、
B、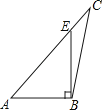 C、
C、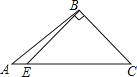 D、
D、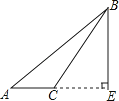 6. 如果 , 下列各式中不一定正确的是( )A、 B、 C、 D、7. 若实数a,b,c在数轴上对应点的位置如图所示,则下列不等式成立的是( )
6. 如果 , 下列各式中不一定正确的是( )A、 B、 C、 D、7. 若实数a,b,c在数轴上对应点的位置如图所示,则下列不等式成立的是( )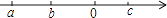 A、ac>bc B、ab>cb C、a+c>b+c D、a+b>c+b8. 小亮用28元钱买了甲、乙两种水果,甲种水果每千克4元,乙种水果每千克6元,且乙种水果比甲种水果少买了2千克,求小亮两种水果各买了多少千克?设小亮买了甲种水果x千克,乙种水果y千克,则可列方程组为( )A、 B、 C、 D、9.
A、ac>bc B、ab>cb C、a+c>b+c D、a+b>c+b8. 小亮用28元钱买了甲、乙两种水果,甲种水果每千克4元,乙种水果每千克6元,且乙种水果比甲种水果少买了2千克,求小亮两种水果各买了多少千克?设小亮买了甲种水果x千克,乙种水果y千克,则可列方程组为( )A、 B、 C、 D、9.如图所示,把一个三角形纸片ABC顶角向内折叠3次之后,3个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )
 A、180° B、270° C、360° D、无法确定10.
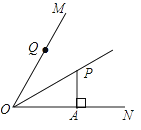
A、180° B、270° C、360° D、无法确定10.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
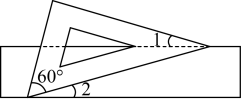
11. 计算:(3x﹣1)(x﹣2)=12. 地球最深的海沟是位于太平洋的马里亚纳大海沟,其最深处海拔 , 该数用科学记数法可表示为 m.13. 命题“对顶角相等”的逆命题是14. 若不等式(a﹣3)x>1的解集为x< ,则a的取值范围是 .15. 如果 与 是同类项,那么xy=.16. 已知2m+5n+3=0,则4m×32n的值为.17. 如图,有一块含有角的直角三角板的两个顶点放在矩形的对边上.如果 , 那么的度数是 .
 18. 若是完全平方式,则 .19. 若一个三角形的三边长分别是 , , , 则x的取值范围是 .
18. 若是完全平方式,则 .19. 若一个三角形的三边长分别是 , , , 则x的取值范围是 .三、解答题
-
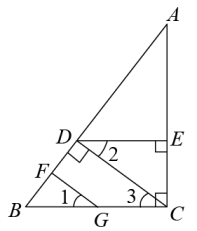
20. 计算:(1)、;(2)、 .21. 把下列各式分解因式:(1)、;(2)、 .22. 解不等式组 ,并写出它的所有整数解.23. 若x+y=3,且(x+2)(y+2)=12.(1)、求xy的值;(2)、求x2+3xy+y2的值.24. 如图,已知:DE⊥AC于E,BC⊥AC,CD⊥AB于D,∠1=∠2,说明:GF⊥AB.
 25. 已知与 , 都是关于x、y的方程y=kx+b的解.(1)、求k、b的值;(2)、若y的值不大于0,求x的取值范围;(3)、若-1≤x<2,求y的取值范围.26. 甲、乙二人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的倍,4分钟两人首次相遇,此时乙还需要跑300米才跑完第一圈,求甲、乙二人的速度及环形场地的周长27. 已知:在△ABC中,AB=AC,∠BAC=90°,点D是BC的中点,点P是BC边上的一个动点,连接AP.直线BE垂直于直线AP,交AP于点E,直线CF垂直于直线AP,交AP于点F.
25. 已知与 , 都是关于x、y的方程y=kx+b的解.(1)、求k、b的值;(2)、若y的值不大于0,求x的取值范围;(3)、若-1≤x<2,求y的取值范围.26. 甲、乙二人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的倍,4分钟两人首次相遇,此时乙还需要跑300米才跑完第一圈,求甲、乙二人的速度及环形场地的周长27. 已知:在△ABC中,AB=AC,∠BAC=90°,点D是BC的中点,点P是BC边上的一个动点,连接AP.直线BE垂直于直线AP,交AP于点E,直线CF垂直于直线AP,交AP于点F.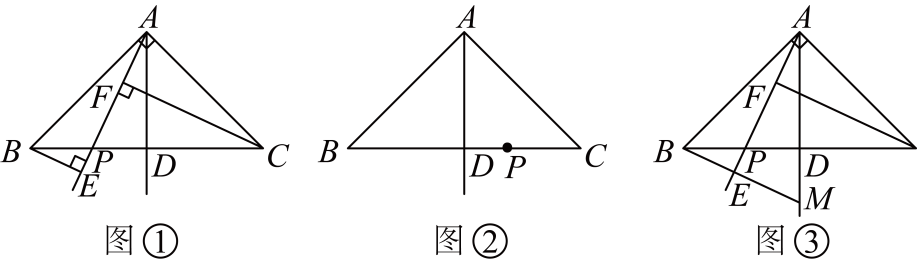 (1)、当点P在BD上时(如图①),求证:CF=BE+EF;(2)、当点P在DC上时(如图②),CF=BE+EF还成立吗?若不成立,请画出图形,并直接写出CF、BE、EF之间的关系(不需要证明).(3)、若直线BE的延长线交直线AD于点M(如图③),找出图中与CP相等的线段,并加以证明.
(1)、当点P在BD上时(如图①),求证:CF=BE+EF;(2)、当点P在DC上时(如图②),CF=BE+EF还成立吗?若不成立,请画出图形,并直接写出CF、BE、EF之间的关系(不需要证明).(3)、若直线BE的延长线交直线AD于点M(如图③),找出图中与CP相等的线段,并加以证明.