江苏省苏州市常熟市等4地2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-10-08 类型：期末考试

进入出卷网下载

一、单选题

1. 计算a³•a²的结果是（）

A、2a⁵ B、a⁵ C、a⁶ D、a⁹

查看试题解析
2. 一元一次不等式 $x + 3 > 5$ 的解集是（）

A、 $x < 2$ B、 $x > - 2$ C、 $x > 2$ D、 $x < - 2$

查看试题解析
3. 一个多边形的每个内角都等于135°，则这个多边形的边数为（）

A、8 B、9 C、10 D、11

查看试题解析
4. 如图，能判断 $A B ∥ E F$ 的条件是（）

A、 $∠ A D E = ∠ C$ B、 $∠ A D E = ∠ D E F$ C、 $∠ A D E = ∠ B$ D、 $∠ A D E = ∠ E F C$

查看试题解析
5. 如图，点B，E，C，F在同一直线上， $A B = D E$ ， $B C = E F$ ，添加一个条件能判定 $△ A B C ≌ △ D E F$ 的是（）

A、 $A B ∥ D E$ B、 $∠ A = ∠ D$ C、 $∠ A C B = ∠ F$ D、 $A C ∥ D F$

查看试题解析
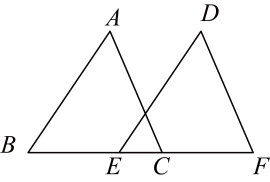6. 若关于x，y的二元一次方程组 ${\begin{array}{l} 2 x - 4 y = 1 - 3 k \\ x + y = 3 \end{array}$ 的解满足 $x - y = 5$ ，则k的值为（）

A、 $- \frac{1}{3}$ B、-1 C、 $- \frac{8}{3}$ D、 $- \frac{11}{3}$

查看试题解析
7. 我国古代数学名著《九章算术》中记载：“今有黄金九枚，白银十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”其译文为：“现有一袋黄金9枚，一袋白银11枚，这两袋的重量恰好相等．若两袋中交换1枚黄金和1枚白银，则原来装黄金的袋子比原来装白银的袋轻13两，问黄金和白银1枚各重几两．”若设1枚黄金重x两，1枚白银重y两，根据题意可列方程组为（）

A、 ${\begin{array}{l} 9 x = 11 y \\ 8 x - 10 y = 13 \end{array}$ B、 ${\begin{array}{l} 9 x = 11 y \\ 10 y - 8 x = 13 \end{array}$ C、 ${\begin{array}{l} 9 x = 11 y \\ (10 y + x) - (8 x + y) = 13 \end{array}$ D、 ${\begin{array}{l} 9 x = 11 y \\ (8 x + y) - (10 y + x) = 13 \end{array}$

查看试题解析
8. 如图，在长方形 $A B C D$ 中， $A B = 8$ ， $B C = 10$ ，点P从点A出发，以每秒1个单位长度的速度沿 $A B$ 向点B匀速运动，点Q从点B出发，以每秒2个单位长度的速度沿 $B C$ 向点C匀速运动，点R从点C出发，以每秒a个单位长度的速度沿 $C D$ 向点D运动，连接 $P Q$ ， $R Q$ ．三点同时开始运动，当某一点运动到终点时，其它点也停止运动，若在某一时刻， $△ P B Q$ 与 $△ Q C R$ 全等，则a的值为（）

A、2或4 B、2或 $\frac{11}{2}$ C、2或 $\frac{5}{2}$ D、2或 $\frac{11}{5}$

查看试题解析

二、填空题

9. x与1的和大于0，用不等式表示为．

查看试题解析
10. 命题“若 $a c > b c$ ，则 $a > b$ ”是命题（填“真”或“假”）．

查看试题解析
11. 若 $a^{m} = 4$ ， $b^{m} = 9$ ，则 ${(a b)}^{m}$ 的值为．

查看试题解析
12. 若 $(x - 3) (x + a) = x^{2} + b x + 18$ ，则 $a + b =$ ．

查看试题解析
13. 如图，在 $△ A B C$ 中，点D、E分别是 $A B$ ， $A C$ 的中点，若 $△ A B C$ 的面积为2，则四边形 $D B C E$ 的面积为．

查看试题解析
14. 已知 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ 是关于x，y的二元一次方程 $a x + b y = 1$ 的解，则 $a^{2} - 4 b^{2} - 4 b + 5 =$ ．

查看试题解析
15. 如图，长方形 $A B C D$ 的周长为12，面积为4．以 $D C$ 为直角边向外作等腰直角三角形 $D C E$ （ $∠ D C E = 90 °$ ），以 $B C$ 为直角边向外作等腰直角三角形 $B C F$ （ $∠ B C F = 90 °$ ），连接 $E F$ ，则五边形 $A B F E D$ 的面积为．

查看试题解析
16. 在 $△ A B C$ 中， $∠ A B C = 2 ∠ C$ ，点D，E分别在边 $B C$ ， $A C$ 上， $∠ A D E = 2 ∠ A E D$ ， $∠ A B C$ 的角平分线与 $∠ A D E$ 的角平分线交于点F，若 $∠ F = 52 °$ ，则 $∠ E D C$ 的度数为°．

查看试题解析

三、解答题

17. 解二元一次方程组： ${\begin{array}{l} 3 x + y = 7 \\ 5 x - 2 y = 8 \end{array}$

查看试题解析
18. 因式分解：

(1)、 $2 {(x + 1)}^{2} - (x + 1)$

(2)、 $3 m^{2} - 27$

查看试题解析
19. 解一元一次不等式组： ${\begin{array}{l} 3 (x - 1) < 5 x - 1 \\ \frac{x + 2}{2} > \frac{1}{3} \end{array}$

查看试题解析
20. 如图，点C是 $∠ A O B$ 边 $O A$ 上一点，过点C作 $C D ∥ O B$ ．

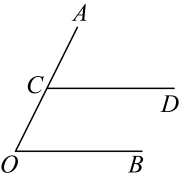(1)、请在图中用无刻度的直尺和圆规作图：作出 $∠ A O B$ 的平分线，交 $C D$ 于点E；（不写保留作图痕迹）

(2)、在（1）的条件下，若 $∠ A C D = 62 °$ ，求 $∠ C E O$ 的度数．

查看试题解析
21. 已知 $3 a^{2} - 7 a - 5 = 0$ ，求 ${(a - 1)}^{2} + \frac{1}{2} a (a - 3)$ 的值．

查看试题解析
22. 已知：如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，过点C作 $C D ⊥ A B$ ，垂足为D．在射线 $C D$ 上截取 $C E = C A$ ，过点E作 $E F ⊥ C E$ ，交 $C B$ 的延长线于点F．

(1)、求证： $△ A B C ≌ △ C F E$ ；

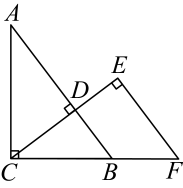(2)、若 $A B = 9$ ， $E F = 4$ ，求 $B F$ 的长．

查看试题解析
23. 观察下列等式：
① $\frac{2^{2} - 1^{2}}{2} = \frac{1}{2} + 1$ ；② $\frac{3^{2} - 2^{2}}{2} = \frac{1}{2} + 2$ ；③ $\frac{4^{2} - 3^{2}}{2} = \frac{1}{2} + 3$ ；④ $\frac{5^{2} - 4^{2}}{2} = \frac{1}{2} + 4$ …

(1)、请按以上规律写出第8个等式；

(2)、猜想并写出第n个等式（n为正整数）；

(3)、证明你猜想的正确性．

查看试题解析
24. 如图，在 $△ A B C$ 中， $C E$ 是 $△ A B C$ 的外角 $∠ A C D$ 的平分线， $C E$ 交 $B A$ 的延长线于点E．

(1)、若 $∠ B = 25 °$ ， $∠ E = 36 °$ ，则 $∠ B A C =$ ；

(2)、若 $∠ B A C = 100 °$ ，且 $∠ E = 2 ∠ B$ ，求 $∠ E$ 的度数．

查看试题解析
25. 某商店需要购进甲、乙两种商品（两种商品均购进），其进价和销售价如下表所示：

甲

乙

进价（元/件）

120

150

售价（元/件）

135

180

(1)、若商店计划购进甲、乙两种商品共30件，正好用去3900元，甲、乙两种商品分别购进多少件？

(2)、若商店计划购进甲、乙两种商品，正好用去1800元，求甲、乙两种商品购进件数的所有方案；

(3)、若商店计划购进甲、乙两种商品共30件，且销售完所有商品后获利不低于785元，求甲商品最多能购进多少件？并求全部售完后的总利润．（利润=售价-进价）

查看试题解析
26. 定义：若一元一次方程的解在一元一次不等式的解集范围内，则称一元一次方程为一元一次不等式的“伴随方程”．如：一元一次方程 $x + 1 = 2$ 的解为 $x = 1$ ，而一元一次不等式 $2 x - 3 < x$ 的解集为 $x < 3$ ，不难发现 $x = 1$ 在 $x < 3$ 范围内，则一元一次方程 $x + 1 = 2$ 是一元一次不等式 $2 x - 3 < x$ 的“伴随方程”

(1)、在① $- 3 (x + 1) = 9$ ， ② $2 x + 3 = 5$ ， ③ $\frac{x + 5}{4} = \frac{1}{2}$ 三个一元一次方程中，是一元一次不等式 $3 (1 + x) > x - 4$ 的“伴随方程”的有（填序号）；

(2)、若关于x的一元一次方程 $3 x - a = 2$ 是关于x一元一次不等式 $3 (a + x) \geq 4 a + x$ 的“伴随方程”，且一元一次方程 $\frac{x - 1}{2} + 1 = x$ 不是关于x的一元一次不等式 $\frac{a}{2} < \frac{a - x}{3}$ 的“伴随方程”．
①求a的取值范围；

②直接写出代数式 $| a | + | a - 3 |$ 的最大值．

查看试题解析
27. 如图1，已知直线 $A B$ 与 $C D$ 相交于点O， $O E$ 平分 $∠ B O C$ ，点G在射线 $O A$ 上，点F在射线 $O C$ 上，且 $E F = E G$ ， $G E$ 交 $O F$ 于点P，若 $O G = 3$ ， $O F = 5$ ．

(1)、求 $△ E O G$ 与 $△ E O F$ 的面积之比；

(2)、比较 $∠ G O F$ 与 $∠ G E F$ 的大小并说明理由；

(3)、如图2，当点M在线段 $O F$ 上，点N在射线 $O D$ 上，且 $E M = E N$ ，试问 $F M + O N$ 的值是否为定值；如果是，求出这个值；如果不是，请说明理由．

查看试题解析

	甲	乙
进价（元/件）	120	150
售价（元/件）	135	180