(单元测试B卷)第五章 二元一次方程组—北师大版2023-2024学年八年级数学上册
试卷更新日期:2023-10-08 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 用代入法解方程组时,将方程代入中,所得的方程正确的是( )A、 B、 C、 D、2. 已知是方程组的解,则的值是( )A、 B、 C、 D、3. 古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思就是说,有一群乌鸦要到树林休息,如果每棵树上落坐有三只乌鸦,则有五个落在地上;如果每棵树上落坐有五只乌鸦,则有一棵树没有乌鸦落坐,请你动脑筋,鸦树各几何?若设乌鸦有只,树有棵,由题意可列方程组( )A、 B、 C、 D、4. 《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,余三;问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,多余3钱,问合伙人数、羊价各是多少?设合伙人数为x人,羊价为y钱,根据题意,可列方程组为( )A、 B、 C、 D、5. 10年前,小明妈妈的年龄是小明的6倍,10年后,小明妈妈的年龄是小明的2倍,小明和他妈妈现在的年龄分别是多少岁?若设小明和他妈妈现在分别是x岁和y岁,根据题意可列方程组为( )A、 B、 C、 D、6. 如图,在Rt△ABO中,∠OAB=90°,B(3,3),点D在边AB上,AD=2BD,点C为OA的中点,点P为边OB上的动点,若四边形PCAD周长最小,则点P的坐标为( )
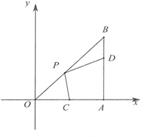 A、( , ) B、(2,2) C、( , ) D、( , )7. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( )
A、( , ) B、(2,2) C、( , ) D、( , )7. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( ) A、 B、 C、 D、8. 已知直线l1:y=kx+b与直线l2:y=-2x+4交于点C(m,2),则方程组的解是( )A、 B、 C、 D、9. 三角形的周长为18cm,第一边与第二边的长度和等于第三边长度的2倍,而它们长度的差等于第三条边长的 ,这个三角形的各边长为( )
A、 B、 C、 D、8. 已知直线l1:y=kx+b与直线l2:y=-2x+4交于点C(m,2),则方程组的解是( )A、 B、 C、 D、9. 三角形的周长为18cm,第一边与第二边的长度和等于第三边长度的2倍,而它们长度的差等于第三条边长的 ,这个三角形的各边长为( )
A、7、5、8 B、7、5、6 C、7、1、9 D、7、8、410. 如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍,如果搭建的正三角形和正六边形共用了2023根火柴,并且正三角形的个数比正六边形的个数多 个,那么能连续搭建的正三角形的个数是( )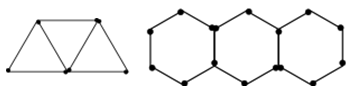 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
11. 三个同学对问题“若方程组的解是 , 求方程组的解”提出各自的想法。甲说:“这个题目条件不够,不能求解”;乙说:“它们的系数有一定规律,可以试试”;丙说“能不能把第二个方程组的两个方程的两边都除以7,通过换元替代的方法来解决”.参考他们的讨论,求出方程组的解是.12. 已知是方程组的解,则代数式 的值为.13. 某餐厅以 、 两种食材,利用不同的搭配方式推出了两款健康餐,其中,甲产品每份含200克 、200克 ;乙产品每份含200克 、100克 .甲、乙两种产品每份的成本价分别为 、 两种食材的成本价之和,若甲产品每份成本价为16元.店家在核算成本的时候把 、 两种食材单价看反了,实际成本比核算时的成本多688元,如果每天甲销量的4倍和乙销量的3倍之和不超过120份,那么餐厅每天实际成本最多为元.14. 已知直线 与直线 的交点坐标为 ,则直线 与直线 的交点坐标为.15. 当m,n是正实数,且满足m+n=mn时,就称点P(m, )为“完美点”.已知点A(1,6)与点B的坐标满足y=﹣x+b,且点B是“完美点”.则点B的坐标是 .
三、解答题(共4题,共20分)
-
16. 小明同学在解方程组 的过程中,错把b看成了6,他其余的解题过程没有出错,解得此方程组的解为 又已知直线y=kx+b过点(3,1),求b的正确值.17. 解方程组 时,本应解出 ,但由于看错了系数c , 而得到解为 ,试求a+b+c的值.18. 小颖家准备装修一套房子,若请甲、乙两个装修公司合作,则需6周完成,需花费工钱5.2万元;若先请甲公司单独做4周后,剩下的请乙公司来做;则还需9周才能完成,需花费工钱4.8万元.若只请一个公司单独完成,从节约开支的角度来考虑,小颖家应该选甲公司还是乙公司?19. 已知一次函数 过点(-2,5),且它的图象与y轴的交点和直线 与y轴的交点关于x轴对称,求这个一次函数的解析式.
四、综合题(共4题,共35分)
-
20. 如图,直线l1过点A(8,0)、B(0,﹣5),直线l2过点C(0,﹣1),l1、l2相交于点D,且△DCB的面积等于8.
 (1)、求点D的坐标;(2)、点D的坐标是哪个二元一次方程组的解.21. 在平面直角坐标系中,若点P的坐标为 , 则定义:为点P到坐标原点O的“折线距离”.
(1)、求点D的坐标;(2)、点D的坐标是哪个二元一次方程组的解.21. 在平面直角坐标系中,若点P的坐标为 , 则定义:为点P到坐标原点O的“折线距离”. (1)、若已知则点P到坐标原点O的“折线距离”;(2)、若点满足 , 且点P到坐标原点O的“折线距离” , 求出P的坐标;(3)、若点P到坐标原点O的“折线距离” , 试在坐标系内画出所有满足条件的点P构成的图形,并求出该图形的所围成封闭区域的面积.22. 如图,直线 与直线 相交于点 .
(1)、若已知则点P到坐标原点O的“折线距离”;(2)、若点满足 , 且点P到坐标原点O的“折线距离” , 求出P的坐标;(3)、若点P到坐标原点O的“折线距离” , 试在坐标系内画出所有满足条件的点P构成的图形,并求出该图形的所围成封闭区域的面积.22. 如图,直线 与直线 相交于点 . (1)、求 , 的值;(2)、垂直于 轴的直线 与直线 , 分别交于点 , , 若线段 的长为 2,求 的值.23. 某县在创建省文明卫生城市中,绿化档次不断提升.某校计划购进A、B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元(1)、求A种、B种树木每棵各多少元?(2)、因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价八折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
(1)、求 , 的值;(2)、垂直于 轴的直线 与直线 , 分别交于点 , , 若线段 的长为 2,求 的值.23. 某县在创建省文明卫生城市中,绿化档次不断提升.某校计划购进A、B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元(1)、求A种、B种树木每棵各多少元?(2)、因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价八折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.