江苏省苏州市2023-2024学年七年级上册数学第一次月考试卷

试卷更新日期：2023-10-08 类型：月考试卷

进入出卷网下载

一、选择题（本大题共8小题，每小题2分，共16分）

1. 下列各数：-（+2），-3² ，（- $\frac{1}{3}$ ）⁴ ， - $\frac{2^{2}}{5}$ ，-（-1）²⁰¹⁵ ， -|-3|中，负数的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 把向北移动记作“+”，向南移动记作“-”，下列说法正确的是（）

A、-5米表示向北移动了5米 B、+5米表示向南移动了5米 C、向北移动-5米表示向南移动5米 D、向南移动5米，也可记作向南移动-5米

查看试题解析
3. 倒数等于它本身的数是（）

A、1 B、0、1 C、-1、1 D、-1、0、1

查看试题解析
4. 下表是某水库一周内水位高低的变化情况（用正数记水位比前一日上升数，用负数记水位比前一日下降数）（单位：m）：

星期一二三四五六日

水位变化 0.12 -0.02 -0.13 -0.20 -0.08 -0.02 0.32

则下列说法正确的有（）

①这个星期的水位总体下降了0.01m；

②本周中星期一的水位最高；

③本周中星期六的水位比星期二下降了0.43m.

A、0个 B、1个 C、2个 D、3个

查看试题解析
5. 数轴上，点A对应的数是﹣6，点B对应的数是﹣2，点O对应的数是0.动点P、Q从A、B同时出发，分别以每秒3个单位和每秒1个单位的速度向右运动.在运动过程中，下列数量关系一定成立的是（　　）

A、PQ＝2OQ B、OP＝2PQ C、3QB＝2PQ D、PB＝PQ

查看试题解析
6. 算式-3-5的结果对应图中的（）

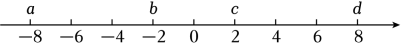A、a B、b C、c D、d

查看试题解析
7. 点M，N在数轴上的位置如图所示，其对应的数分别是m和n.对于以下结论：
①n-m＞0，②mn＞0，③|m|＞|n|，④-m＞n.其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 设abc≠0，且a+b+c＝0，则 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} + \frac{a b c}{| a b c |}$ 的值可能是（）

A、0 B、±1 C、±2 D、0或±2

查看试题解析

二、填空题（本大题共10小题，每小题2分，共20分）请把答案直接填写在横线上

9. -5的相反数等于.

查看试题解析
10. 比较大小：-（ $- 1 \frac{3}{5}$ ）-|-1.35|.（填“＜”、“＞”或“＝”）

查看试题解析
11. 把（-12）-（-13）+（-14）统一成加法的形式是，写成省略加号的形式是.

查看试题解析
12. $- 1 - \frac{1}{2}$ ＝.

查看试题解析
13. 两个数a与2在数轴上对应的点之间的距离为3，已知b²＝4，且a＜b，则a﹣b的值为.

查看试题解析
14. 甲数相当于乙数的 $\frac{5}{6}$ ，甲数是30，则乙数是.

查看试题解析
15. 若|x|＝5，|y|＝4，且xy＜0，则x-y的值为.

查看试题解析
16. 已知x，y互为相反数，a，b互为倒数，c的绝对值为3，则x+y+ab+|c|的值是.

查看试题解析
17. 如图，是北京S1线地铁的分布示意图，其中桥户营、四道桥、金安桥、苹果园四站在同一条直线上.如果在图中以正东为正方向建立数轴，桥户营站、苹果园站表示的数分别是-4，2，那么金安桥站表示的数是.

查看试题解析
18. 已知：如图所示，A、B是数轴上的两个点，点A所表示的数为-5，动点P以每秒4个单位长度的速度从点B向左运动，同时，动点Q、M从点A向右运动，且点M的速度是点Q速度的 $\frac{1}{3}$ ，当运动时间为2秒和4秒时，点M和点P的距离都是6个单位长度，则当点P运动到点A时，动点Q所表示的数为.

查看试题解析

三、解答题（本大题共8小题，共64分）.解答时应写出文字说明、证明过程或演算步骤.

19. 计算：

(1)、 $(\frac{2}{9} - \frac{1}{3} + \frac{3}{5})$ ×45

(2)、（-8）÷（-2³）×（ $\frac{1}{2} - 2$ ）+1.

查看试题解析
20. 如果xⁿ＝y，那么我们记为：（x，y）＝n.例如3²＝9，则（3，9）＝2.

(1)、根据上述规定，填空：（2，8）＝，（-5，25）＝；

(2)、若（x，16）＝2，则x＝；

(3)、若（4，a）＝2，（b，8）＝3，求（b，a）的值.

查看试题解析
21. 世界最高峰珠穆朗玛峰的海拔高度是8844.43米，死海湖面的海拔高度是-416米，我国吐鲁番盆地的海拔高度比死海湖面高262米，珠穆朗玛峰的海拔高度比吐鲁番盆地的海拔高度高多少米？

查看试题解析
22. 如图，在数轴上有A，B两点，其中点A在点B的左侧，已知点B对应的数为4，点A对应的数为a.

(1)、若a＝ $\frac{7}{6} \times (\frac{1}{6} - \frac{1}{3}) \times \frac{3}{14} \div \frac{3}{5}$ ×72，则线段AB的长为（直接写出结果）.

(2)、若点C在射线AB上（不与A，B重合），且2AC-3BC＝6，求点C对应的数（结果用含a的式子表示）.

(3)、若点M在线段AB之间，点N在点A的左侧（M、N均不与A、B重合），且AM-BM＝2.当 $\frac{A M}{A N}$ ＝3，BN＝6BM时.求a的值.

查看试题解析
23. 一个外卖小哥骑摩托车从沃尔玛出发，在东西向的大道上送外卖.如果规定向东行驶为正，向西行驶为负，一天中外卖小哥的七次行驶记录如下（单位：km）：-7，+8，-4，+6，+5，-2，-9

(1)、填空：第次送外卖时距沃尔玛最远.

(2)、求七次外卖送完时小哥在沃尔玛的什么方向？距沃尔玛多远？

(3)、若每千米耗油0.2升，问这七次送外卖共耗油多少升？

查看试题解析
24. 把下列各数分别在数轴上表示出来，并用“＜”连接起来：
- $\frac{1}{2}$ ，2，0，-3，|-0.5|，-（-4 $\frac{1}{2}$ ）

＜＜＜＜＜.

查看试题解析
25. 已知买入股票与卖出股票均需支付成交金额的0.5%的交易手续费，李先生上周在股市以收盘价每股20元买进某公司的股票1000股，如表为在本周交易日内，该股票每股的涨跌情况：
时间星期一星期二星期三星期四星期五
每股涨跌/元 +2 +3 -2.5 +3 -2
注：①涨记作“+”，跌记作“-”；
②表中记录的数据为每天收盘价格相比前一天收盘价格的变化.

(1)、直接判断本周内价格最高的是星期.

(2)、求本周三收盘时，该股票每股多少钱？

(3)、若李先生在本周五以收盘价将全部股票卖出，李先生周五当天需要支付多少元的交易手续费？

查看试题解析
26. 如图：在数轴上A点表示数a，B点表示数b，C点表示数c，b是最小的正整数，且a，c满足|a+2|+（c-7）²＝0.

(1)、a＝， b＝， c＝；

(2)、若将数轴折叠，使得A点与C点重合，则点B与数表示的点重合；

(3)、点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，则AB＝， AC＝， BC＝.（用含t的代数式表示）

(4)、请问：3BC-2AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值.

查看试题解析

星期	一	二	三	四	五	六	日
水位变化	0.12	-0.02	-0.13	-0.20	-0.08	-0.02	0.32

时间	星期一	星期二	星期三	星期四	星期五
每股涨跌/元	+2	+3	-2.5	+3	-2