江苏省南京市鼓楼区五校2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-10-08 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 中国大陆芯片领域的龙头企业“中芯国际”目前已经实现14nm(0.00000014m)工艺芯片的量产,使中国集成电路制造技术与世界最先进工艺拉近了距离.数据0.000000014用科学记数法表示为( )A、 B、 C、 D、3. 下列式子从左到右的变形是因式分解的是( )A、 B、 C、 D、4. 若 , 则下列不等式中不成立的是( )A、 B、 C、 D、5. 如图,把一张长方形纸片 沿 折叠, ,则 ( )
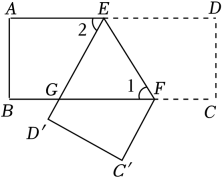 A、 B、 C、 D、6. 有4张长为、宽为的长方形纸片,按如图的方式拼成一个边长为的正方形,图中阴影部分的面积为 , 空白部分的面积为 . 若 , 则、满足( )
A、 B、 C、 D、6. 有4张长为、宽为的长方形纸片,按如图的方式拼成一个边长为的正方形,图中阴影部分的面积为 , 空白部分的面积为 . 若 , 则、满足( )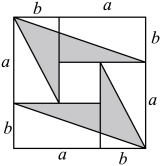 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 计算: .8. a与3的和是正数,用不等式表示为.9. 写出一个解为 的二元一次方程是 .10. 计算: .11. 已知 , , 则的值为 .12. 如图,直线a,b被直线c所截,且a∥b,∠1= , 则∠2的度数为 .
 13. 写出命题“如果 ,那么 互为倒数”的逆命题:.14. 把方程2x﹣y=1化为用含x的代数式表示y的形式:y=.15. 若关于的不等式组恰有个整数解,则实数的取值范围是 .16. 如图,把图(a)称为二环三角形,它的内角和∠A+∠B+∠C+∠A1+∠B1+∠C1;把图(b)称为二环四形边,它的内角和∠A+∠B+∠C+∠D+∠A1+∠B1+∠C1+∠D1⋯⋯;依此规律,请你探究:二环n边形的内角和为 度.(用含n的式子表示)
13. 写出命题“如果 ,那么 互为倒数”的逆命题:.14. 把方程2x﹣y=1化为用含x的代数式表示y的形式:y=.15. 若关于的不等式组恰有个整数解,则实数的取值范围是 .16. 如图,把图(a)称为二环三角形,它的内角和∠A+∠B+∠C+∠A1+∠B1+∠C1;把图(b)称为二环四形边,它的内角和∠A+∠B+∠C+∠D+∠A1+∠B1+∠C1+∠D1⋯⋯;依此规律,请你探究:二环n边形的内角和为 度.(用含n的式子表示)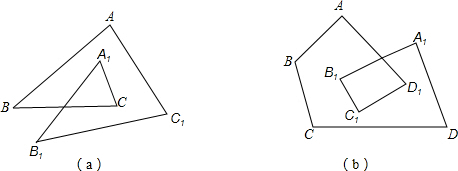
三、解答题
-
17. 计算和化简:(1)、;(2)、 .18. 先化简,再求值: , 其中 .19. 因式分解:(1)、;(2)、 .20.(1)、解方程组;(2)、解不等式组 , 并写出它的整数解.21. 如图,在中,点 , 在边上,点在边上, , 点在边上,且 .
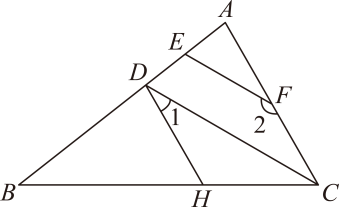 (1)、求证:;(2)、若平分 , , 求的度数.22. 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.仅用无刻度的直尺完成下列作图.
(1)、求证:;(2)、若平分 , , 求的度数.22. 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.仅用无刻度的直尺完成下列作图.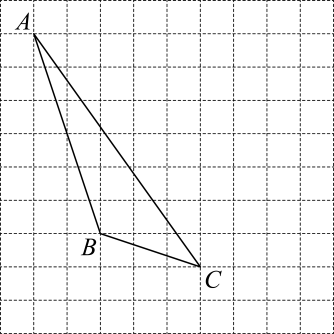 (1)、画出向右平移4个单位后的图形(注意标上字母);(2)、画出的中线(注意标上字母);(3)、在图中存在满足与面积相等的格点Q(与点A不重合).共计有 ▲ 个.23. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气.”某校为提高学生的阅读品味,现决定购买获得矛盾文学奖的甲、乙两种书共100本,已知购买2本甲种书和1本乙种书共需100元,购买3本甲种书和2本乙种书共需165元.(1)、求甲,乙两种书的单价分别为多少元:(2)、若学校决定购买以上两种书的总费用不超过3200元,那么该校最多可以购买甲种书多少本?24. 配方法是数学中非常重要的一种思想方法,它是指将一个式子或将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法,这种方法常被用到代数式的变形中,并结合非负数的意义来解决问题.
(1)、画出向右平移4个单位后的图形(注意标上字母);(2)、画出的中线(注意标上字母);(3)、在图中存在满足与面积相等的格点Q(与点A不重合).共计有 ▲ 个.23. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气.”某校为提高学生的阅读品味,现决定购买获得矛盾文学奖的甲、乙两种书共100本,已知购买2本甲种书和1本乙种书共需100元,购买3本甲种书和2本乙种书共需165元.(1)、求甲,乙两种书的单价分别为多少元:(2)、若学校决定购买以上两种书的总费用不超过3200元,那么该校最多可以购买甲种书多少本?24. 配方法是数学中非常重要的一种思想方法,它是指将一个式子或将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法,这种方法常被用到代数式的变形中,并结合非负数的意义来解决问题.定义:若一个整数能表示成(a,b为整数)的形式,则称这个数为“完美数”.
例如,5是“完美数”,理由:因为 , 所以5是“完美数”.
解决问题:
(1)、已知29是“完美数”,请将它写成(a,b为整数)的形式;(2)、若可配方成(m,n为常数),求mn的值;(3)、已知(x,y是整数,k是常数),要使S为“完美数”,试求出k值.25. 已知不等式组(1)、当时,它的解集是:;(2)、当时,它的解集是:;(3)、当时,它的解集是: .(4)、由(1)(2)(3)当k的值发生变化时,原不等式组的解集也发生变化,试根据k值的变化情况,写出原不等式组的解集.26. 如图,直线 , 一副三角板( , , , )按如图①放置,其中点E在直线上,点B,C均在直线上,且平分 .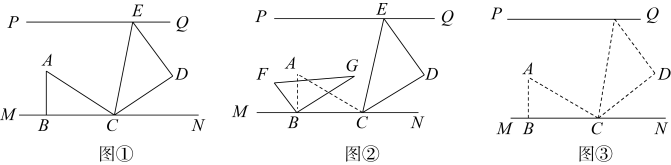 (1)、求的度数;(2)、如图②,若将绕B点以每秒5°的速度按逆时针方向旋转(A,C的对应点分别为F,G).设旋转时间为t秒;
(1)、求的度数;(2)、如图②,若将绕B点以每秒5°的速度按逆时针方向旋转(A,C的对应点分别为F,G).设旋转时间为t秒;①在旋转过程中,若边 , 求t的值;
②若在绕B点旋转的同时,绕E点以每秒4°的速度按顺时针方向旋转.请直接写出旋转过程中有一边与平行时t的值.