湖北省武汉市硚口区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-10-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，最大的数是（）

A、3 B、1 C、 $- 3$ D、 $π$

查看试题解析
2. 式子 $\sqrt{x - 2}$ 中，x的取值范围是（）

A、 $x \geq 2$ B、 $x > 2$ C、 $x \geq 0$ D、 $x > 0$

查看试题解析
3. 下列调查中，最适合采用全面调查的是（）

A、乘坐地铁前的安检 B、检测武汉东湖的水质 C、检测一批电池的使用寿命 D、调查某市家庭人均收入

查看试题解析
4. 点 $(4 ， - 2)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 如图，点E在AC的延长线上，下列条件中不能判断AB∥CD的是（）

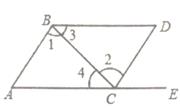A、∠A=∠DCE B、∠1=∠2 C、∠3=∠4 D、∠D+∠ABD=180°

查看试题解析
6. 一副直角三角板如图放置，点 $C$ 在 $F D$ 的延长线上， $A B ∥ C F$ ， $∠ F = ∠ A C B = 90 °$ ， $∠ A = 60 °$ ， $∠ E = 45 °$ ，则 $∠ D B C$ 的度数为（）

A、 $10 °$ B、 $15 °$ C、 $20 °$ D、 $25 °$

查看试题解析
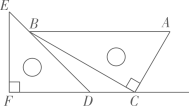7. 若 $a \neq 0$ ，下列不等式一定成立的是（）

A、 $2023 - a > 2022 + a$ B、 $- 2023 a > - 2022 a$ C、 $\frac{2023}{a} > \frac{2022}{a}$ D、 $- a - 2023 < - a - 2022$

查看试题解析
8. 甲、乙二人都以不变的速度在环形路上跑步，如果同时同地出发，反向而行，每隔2 $m i n$ 相遇一次；如果同时同地出发，同向而行，每隔6 $m i n$ 相遇一次，已知甲比乙跑得快，则甲每分跑（）

A、 $\frac{1}{2}$ 圈 B、 $\frac{1}{3}$ 圈 C、 $\frac{1}{4}$ 圈 D、 $\frac{1}{6}$ 圈

查看试题解析
9. 已知关于x的不等式组 ${\begin{array}{l} - x + a > 2 \\ x - \frac{x - 5}{2} \geq - 1 \end{array}$ 的最大整数解和最小整数解互为相反数，则a的取值范围是（）

A、 $9 < a < 10$ B、 $9 \leq a \leq 10$ C、 $9 < a \leq 10$ D、 $9 \leq a < 10$

查看试题解析
10. 在平面直角坐标系中，横、纵坐标都是整数的点称为整点，已知 $A (n ， n)$ ， $B (- \frac{n}{2} ， n)$ ， n为正整数，且线段AB上共有2024个整点，则n的值是（）

A、1348 B、1349 C、1011 D、1012

查看试题解析

二、填空题

11. 计算： $\sqrt{16}$ = ．

查看试题解析
12. 如图是某同学6次数学测验成绩的折线统计图，则该同学这6次成绩的最低分是分.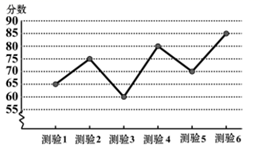

查看试题解析
13. 1号仓库与2号仓库共存粮 $280$ 吨，现从1号仓库运出存粮的 $30 %$ ，放入2号仓库后，此时2号仓库存粮恰好等于1号仓库所余存粮，则1号仓库原来存粮吨．

查看试题解析
14. 点 $A (6 - 2 x ， x - 3)$ 在x轴的上方，将点A向上平移4个单位长度，再向左平移1个单位长度后得到点B，点B到x轴的距离大于点B到y轴的距离，则x的取值范围是．

查看试题解析
15. 我国古代的《张丘建算经》中有著名的“百鸡问题”，原文是：“今有鸡翁一值钱五，鸡母一值钱三，鸡雏三值钱一，凡百钱买鸡百只，问鸡翁、母、雏各几何？”意思是说“公鸡每只值五文钱，母鸡每只值三文钱，小鸡每三只值一文钱，现在用一百文钱买一百只鸡，问这一百只鸡中，公鸡、母鸡、小鸡各有多少只？”则此“百鸡问题”共有种购买方案（每种鸡至少购买一只）．

查看试题解析
16. 如图，在三角形 $A B C$ 中，点D，E是边 $A C$ 上两点，点F在边AB 上，将三角形 $B D C$ 沿 $B D$ 折叠得三角形 $B D G$ ， $D G$ 交 $A B$ 于点H，将三角形 $E F A$ 沿 $E F$ 折叠恰好得到三角形 $E F H$ ，且 $H E ∥ B D$ ．下列四个结论：① $∠ E H D = ∠ H E D$ ；② $∠ A = ∠ A D H$ ；③ $∠ E H D = 2 ∠ H B D$ ；④若 $4 ∠ A B C = 3 ∠ A H D$ ，则 $∠ A B D = 4 ∠ A B G$ ．其中正确的结论是（填写序号）．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} 3 x - 4 < 2 ， ① \\ 2 x + 2 \geq x ， ② \end{array}$ 请按下列步骤完成解答：

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来；

(4)、原不等式组的解集是.

查看试题解析
18. 解下列方程组：

(1)、 ${\begin{array}{l} x - y = 18 \\ x = 6 y - 7 \end{array}$

(2)、 ${\begin{array}{l} 4 x + y = 15 \\ 3 x - 4 y = - 3 \end{array}$

查看试题解析
19. 某市举办青少年禁毒知识竞赛活动，某校举办选拔赛后，随机抽取了部分学生的成绩，按成绩（百分制）分为A、B、C、D四个等级，并绘制了如下不完整的统计图表．
等级
成绩（x）
人数
A
          $90 < x \leq 100$
m
B
          $80 < x \leq 90$
24
C
          $70 < x \leq 80$
14
D
          $x \leq 70$
10

根据图表信息，回答下列问题：

(1)、本次调查的样本容量是，表中 $m =$ ；

(2)、在扇形统计图中，B等级对应的圆心角的大小是；

(3)、在扇形统计图中若全校有1800人参加了此次选拔赛，请估计成绩为C等级的人数．

查看试题解析
20. 如图，在三角形ABC中，点D，E分别在 $A C ， A B$ 上，点F，G在 $B C$ 上， $E F$ 与 $D G$ 交于点O， $D E ∥ B C$ ， $∠ B = ∠ 3$ ．

(1)、求证： $∠ 1 + ∠ 2 = 180 °$ ；

(2)、若 $E D$ 平分 $∠ A E F$ ， $∠ C F E = 2 ∠ 1$ ，求 $∠ 2$ 的大小．

查看试题解析
21. 如图是由小正方形组成的 $10 \times 10$ 网格，每个小正方形的顶点叫做格点，三角形 $A B C$ 的三个原点及点O都是格点，其中O点是坐标原点，点 $A^{'}$ 的坐标为 $（ 1 ， 3 ）$ ，现将三角形 $A B C$ 沿 $A A^{'}$ 的方向平移，得到对应三角形 $A^{'} B^{'} C^{'}$ ．

(1)、画三角形 $A^{'} B^{'} C^{'}$ ，直接写出点 $B^{'}$ 的坐标是，点 $C^{'}$ 的坐标是．

(2)、连接 $B^{'} C$ ， $B B^{'}$ ，已知三角形 $B B^{'} C$ 为等腰直角三角形， $∠ B C B^{'} = 90 °$ ，点D为线段 $B C$ 上动点，则 $B^{'} C$ 的值是， $A D$ 的最小值是；

(3)、已知 $B M ∥ x$ 轴，三角形 $B^{'} C^{'} M$ 的面积和三角形 $A B C$ 的面积相等，直接写出所有点M的坐标．

查看试题解析
22. 某服装店同时购进A，B两款夏装，进价和售价如下表所示，已知购买A款30套和B款20套，共需3400元：购买A款20套和B款30套，共需3600元．
夏装款式
A款
B款
每套进价（单价：元）
a
b
每套售价（单价：元）
100
150

(1)、求a，b的值；

(2)、该服装店计划购买A，B两款夏装共300套，其中B款套数不低于A款套数的一半，购买总金额不多于21000元，设购买A款x套．
①求x的取值范围：
②求该店的售完A、B两款服装可获得的最大利润与最小利润．

查看试题解析
23. 如图1，已知直线 $P Q$ 分别与直线 $A B ， C D$ 交于点P和点Q， $A B ⊥ P Q$ ， $C D ⊥ P Q$ ．

(1)、求证： $A B ∥ C D$ ；

(2)、如图2，P，Q两点分别沿直线 $A B$ 和 $C D$ 向左平移相同的单位长度得到E，F两点，点G在直线 $P Q$ 上运动， $E M$ 平分 $∠ A E G$ ，点H在直线 $E M$ 上，连接 $F H ， G F$ 的延长线交 $E M$ 于点N， $F N$ 平分 $∠ C F H$ ．
①若 $∠ C F H < 90 °$ ， $2 ∠ E H F + ∠ E G F = 255 °$ ，求 $∠ C F H$ 的大小；
②当点G在 $A B ， C D$ 之间时，直接写出 $∠ E N F$ ， $∠ E G F$ ， $∠ E H F$ 之间的数量关系．

查看试题解析
24. 已知 $\sqrt{b - 5} + | b - c - 8 | = 0$ ， d为4的算术平方根，点 $A (a ， b)$ ， $B (a - d ， b - 3)$ ， $C (c ， 0)$ ，且 $a > 0$ ．

(1)、直接写出 $b =$ ， $c =$ ， $d =$ ；

(2)、如图1，若点C在直线AB上，求a的值；

(3)、平移线段AB，点A的对应点M在y轴的正半轴上，点B的对应点N恰好在x轴的负半轴上，点P以每秒3个单位长度从点M向y轴负半轴运动，同时，点Q以每秒2个单位长度从N点向x轴正半轴运动，直线NP，MQ交于点D，设点P，Q运动的时间为t秒．
①如图2，当 $1 < t < 2$ 时，探究三角形MPD的面积和三角形NQD的面积的数量关系，并说明理由；
②若三角形MDN的面积为10，直接写出点D的坐标．

查看试题解析

等级	成绩（x）	人数
A	$90 < x \leq 100$	m
B	$80 < x \leq 90$	24
C	$70 < x \leq 80$	14
D	$x \leq 70$	10

夏装款式	A款	B款
每套进价（单价：元）	a	b
每套售价（单价：元）	100	150