湖南省衡阳市衡南县2023年中考三模数学试题
试卷更新日期:2023-10-07 类型:中考模拟
一、单选题
-
1. 据不完全统计,截至2020年4月2号,华为官方应用市场“学习强国”下载量已达88300000次.将数据88300000用科学记数法表示为( )A、 B、 C、 D、2. 下列图形,既是中心对称图形又是轴对称图形的是( )A、
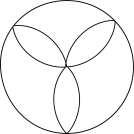 B、
B、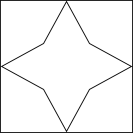 C、
C、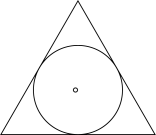 D、
D、 3. 若 , , 则的值为( )A、 B、21 C、 D、104. 下列计算正确的是A、 B、 C、 D、5. 在下面的四个几何体中,同一几何体的主视图与俯视图相同的是( )A、
3. 若 , , 则的值为( )A、 B、21 C、 D、104. 下列计算正确的是A、 B、 C、 D、5. 在下面的四个几何体中,同一几何体的主视图与俯视图相同的是( )A、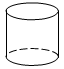 B、
B、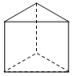 C、
C、 D、
D、 6. 不等式组 的解集在数轴上表示正确的是( )A、
6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、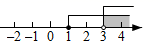 D、
D、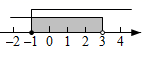 7. 已知 是方程组 的解,则 的值是( )A、﹣1 B、1 C、﹣5 D、58. 某中学八(1)班8个同学在课间进行一分钟跳绳比赛,成绩(单位:个)如下:115,138,126,143,134,126,157,118.这组数据的众数和中位数分别是( )A、126,126 B、126,130 C、130,134 D、118,1349. 如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是( )
7. 已知 是方程组 的解,则 的值是( )A、﹣1 B、1 C、﹣5 D、58. 某中学八(1)班8个同学在课间进行一分钟跳绳比赛,成绩(单位:个)如下:115,138,126,143,134,126,157,118.这组数据的众数和中位数分别是( )A、126,126 B、126,130 C、130,134 D、118,1349. 如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是( )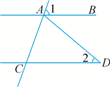 A、20° B、35° C、40° D、70°10. 如图,四边形与四边形位似,其位似中心为点 , 且 , 则( )
A、20° B、35° C、40° D、70°10. 如图,四边形与四边形位似,其位似中心为点 , 且 , 则( )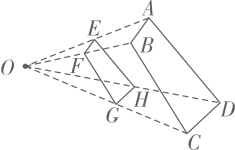 A、 B、 C、 D、11. 如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC . 若∠BCD=50°,则∠AOC的度数为( )
A、 B、 C、 D、11. 如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC . 若∠BCD=50°,则∠AOC的度数为( )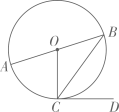 A、40° B、50° C、80° D、100°12. 已知二次函数 的图象如图所示,对于下列结论:① ;② ;③ ;④ ;⑤方程 的根是 , ,其中正确结论的个数是( )
A、40° B、50° C、80° D、100°12. 已知二次函数 的图象如图所示,对于下列结论:① ;② ;③ ;④ ;⑤方程 的根是 , ,其中正确结论的个数是( )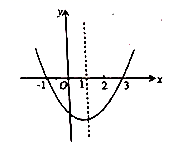 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
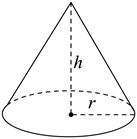
13. 若二次根式 有意义,则x的取值范围是 .14. 分解因式: .15. 如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为(结果保留).
 16. 观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第6个图中共有点的个数是.
16. 观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第6个图中共有点的个数是.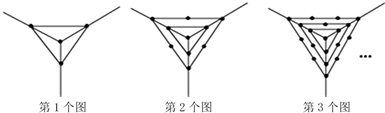 17. 在中,直径 , 弦于 , , 则弦的长为 .
17. 在中,直径 , 弦于 , , 则弦的长为 .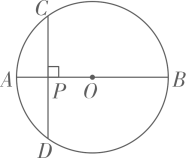 18. 如图,有两张矩形纸片ABCD和EFGH , AB=EF=2cm,BC=FG=8cm.把纸片ABCD交叉叠放在纸片EFGH上,使重叠部分为平行四边形,且点D与点G重合.当两张纸片交叉所成的角α最小时,tanα等于 .
18. 如图,有两张矩形纸片ABCD和EFGH , AB=EF=2cm,BC=FG=8cm.把纸片ABCD交叉叠放在纸片EFGH上,使重叠部分为平行四边形,且点D与点G重合.当两张纸片交叉所成的角α最小时,tanα等于 .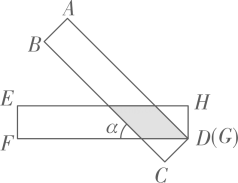
三、解答题
-
19. 计算: .20. 如图,BD是▱ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.
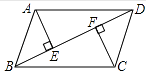 21. 某校为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调查结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成如图所示的两幅不完整的统计图:根据图中信息,解答下列问题:
21. 某校为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调查结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成如图所示的两幅不完整的统计图:根据图中信息,解答下列问题: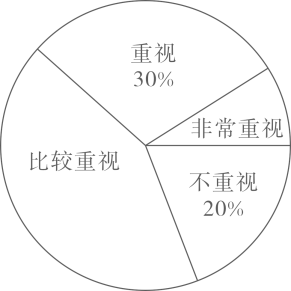
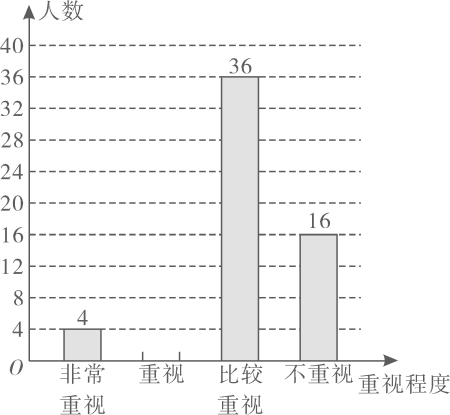 (1)、在扇形统计图中,“比较重视”所占的圆心角的度数为 , 并补全条形统计图;(2)、该校共有学生2400人,请你估计该校对视力保护“非常重视”的学生人数;(3)、对视力“非常重视”的4人有一名男生,三名女生,若从中随机抽取两人向全校作视力保护经验交流,请利用树状图或列表法,求出恰好抽到都是女生的概率.22. 如图,某大楼的顶部树有一块广告牌 , 小李在山坡的坡脚处测得广告牌底部的仰角为 . 沿坡面向上走到处测得广告牌顶部的仰角为 , 已知山坡的坡度 , 米,米.
(1)、在扇形统计图中,“比较重视”所占的圆心角的度数为 , 并补全条形统计图;(2)、该校共有学生2400人,请你估计该校对视力保护“非常重视”的学生人数;(3)、对视力“非常重视”的4人有一名男生,三名女生,若从中随机抽取两人向全校作视力保护经验交流,请利用树状图或列表法,求出恰好抽到都是女生的概率.22. 如图,某大楼的顶部树有一块广告牌 , 小李在山坡的坡脚处测得广告牌底部的仰角为 . 沿坡面向上走到处测得广告牌顶部的仰角为 , 已知山坡的坡度 , 米,米. (1)、求点距水平面的高度;(2)、求广告牌的高度.23. 国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:(1)、用表达式表示蝙蝠型风筝销售量(个)与售价(元)之间的函数关系();(2)、王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?24. 如图,在中, , 的平分线交边于点 . 以上一点为圆心作 , 使经过点和点 .
(1)、求点距水平面的高度;(2)、求广告牌的高度.23. 国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:(1)、用表达式表示蝙蝠型风筝销售量(个)与售价(元)之间的函数关系();(2)、王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?24. 如图,在中, , 的平分线交边于点 . 以上一点为圆心作 , 使经过点和点 . (1)、判断直线与的位置关系,并说明理由.(2)、若 , .
(1)、判断直线与的位置关系,并说明理由.(2)、若 , .①求的半径;
②设与边的另一个交点为 , 求线段 , 与劣弧所围成的阴影部分的面积.(结果保留根号和)
25. 已知,把 和 按图1摆放, 点C与E点重合 ,点B、C、E、F始终在同一条直线上, , , , , ,如图2, 从图1的位置出发,以每秒1个单位的速度沿CB方向匀速移动,同时,点P从A出发,沿AB以每秒1个单位向点B匀速移动,AC与 的直角边相交于Q,当P到达终点B时, 同时停止运动连接PQ,设移动的时间为 解答下列问题: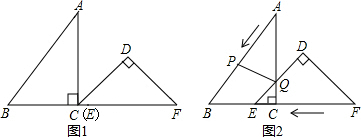 (1)、 在平移的过程中,当点D在 的AC边上时,求AB和t的值;(2)、在移动的过程中,是否存在 为等腰三角形?若存在,求出t的值;若不存在,说明理由.26. 已知,二次函数y=-x2+x+2图象与x轴交于A、B两点,与y轴交于点C , 连接AC、BC .
(1)、 在平移的过程中,当点D在 的AC边上时,求AB和t的值;(2)、在移动的过程中,是否存在 为等腰三角形?若存在,求出t的值;若不存在,说明理由.26. 已知,二次函数y=-x2+x+2图象与x轴交于A、B两点,与y轴交于点C , 连接AC、BC .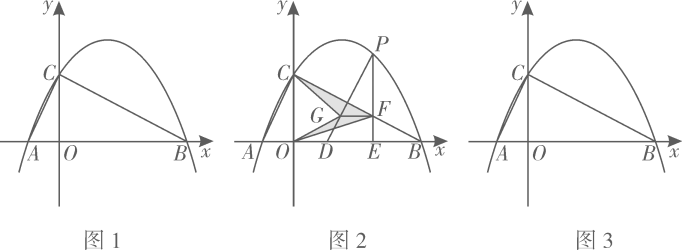 (1)、如图1,请判断△ABC的形状,并说明理由;(2)、如图2,D为线段AB上一动点,作DP∥AC交抛物线于点P , 过P作PE⊥x轴,垂足为E , 交BC于点F , 过F作FG⊥PE , 交DP于G , 连接CG , OG , 求阴影部分面积S的最大值和D点坐标;(3)、如图3,将抛物线沿射线AC方向移动个单位得到新的抛物线y′=ax2+bx+c(a≠0),是否在新抛物线对称轴上存在点M , 在坐标平面内存在点N , 使得以C、B、M、N为顶点的四边形是以CB为边的矩形?若存在,请直接写出N点坐标;若不存在,请说明理由.
(1)、如图1,请判断△ABC的形状,并说明理由;(2)、如图2,D为线段AB上一动点,作DP∥AC交抛物线于点P , 过P作PE⊥x轴,垂足为E , 交BC于点F , 过F作FG⊥PE , 交DP于G , 连接CG , OG , 求阴影部分面积S的最大值和D点坐标;(3)、如图3,将抛物线沿射线AC方向移动个单位得到新的抛物线y′=ax2+bx+c(a≠0),是否在新抛物线对称轴上存在点M , 在坐标平面内存在点N , 使得以C、B、M、N为顶点的四边形是以CB为边的矩形?若存在,请直接写出N点坐标;若不存在,请说明理由.