(北师大版)2023-2024学年八年级数学上册5.7 用二元一次方程组确定一次函数表达式 同步测试
试卷更新日期:2023-10-07 类型:同步测试
一、选择题
-
1. 已知二元一次方程组的解为 , 则在同一平面直角坐标系中,直线:与直线:的交点坐标为( )A、 B、 C、 D、2. 如图,直线与直线相交于点 , 则关于的方程组的解为( )
 A、 B、 C、 D、3. 已知直线与直线在同一平面直角坐标系中交于点 , 那么关于x,y的方程组的解是( )A、 B、 C、 D、4. 若直线y=-x+m与直线y=2x+4的交点在第二象限,则m的取值范围是( )A、 B、 C、 D、5. 如图,直线与交点的横坐标为1,则关于x、y的二元一次方程组的解为( )
A、 B、 C、 D、3. 已知直线与直线在同一平面直角坐标系中交于点 , 那么关于x,y的方程组的解是( )A、 B、 C、 D、4. 若直线y=-x+m与直线y=2x+4的交点在第二象限,则m的取值范围是( )A、 B、 C、 D、5. 如图,直线与交点的横坐标为1,则关于x、y的二元一次方程组的解为( ) A、 B、 C、 D、6. 函数y=ax+b与函数y=cx+d的图象是两条相交直线,则二元一次方程组有( )解.A、0个 B、1个 C、2个 D、3个7. 如图,点的坐标为 , 直线与轴交于点 , 与轴交于点 , 点在直线上运动.当线段最短时,求点的坐标( )
A、 B、 C、 D、6. 函数y=ax+b与函数y=cx+d的图象是两条相交直线,则二元一次方程组有( )解.A、0个 B、1个 C、2个 D、3个7. 如图,点的坐标为 , 直线与轴交于点 , 与轴交于点 , 点在直线上运动.当线段最短时,求点的坐标( ) A、 B、 C、 D、8. 下列图象中,以方程﹣2x+y﹣2=0的解为坐标的点组成的图象是( )A、
A、 B、 C、 D、8. 下列图象中,以方程﹣2x+y﹣2=0的解为坐标的点组成的图象是( )A、 B、
B、 C、
C、 D、
D、 9. 一次函数的图象与正比例函数的图象都经过点(-3,2),则方程组的解为( )A、 B、 C、 D、10. 如图,一次函数y=2x+1的图象与y=kx+b的图象相交于点A,则方程组的解是( )
9. 一次函数的图象与正比例函数的图象都经过点(-3,2),则方程组的解为( )A、 B、 C、 D、10. 如图,一次函数y=2x+1的图象与y=kx+b的图象相交于点A,则方程组的解是( )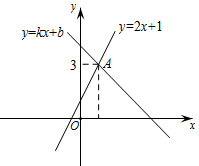 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,已知直线和直线交于点 , 若二元一次方程组的解为、 , 则关于.
 12. 如图所示, 在平面直角坐标系 中,直线和直线的交点坐标为 , 则二元一次方程组的解是.
12. 如图所示, 在平面直角坐标系 中,直线和直线的交点坐标为 , 则二元一次方程组的解是. 13. 已知一次函数与图象的交点是 , 则方程组的解是 .14. 已知:直线与直线的图象交点如图所示,则方程组的解为 .
13. 已知一次函数与图象的交点是 , 则方程组的解是 .14. 已知:直线与直线的图象交点如图所示,则方程组的解为 . 15. 如图,若一次函数与正比例函数的图象交于点 , 则方程组的解为 .
15. 如图,若一次函数与正比例函数的图象交于点 , 则方程组的解为 .
三、解答题
-
16. 已知:如图1,在平面直角坐标系中,直线 : 与坐标轴分别相交于点A、B与 : 相交于点C.
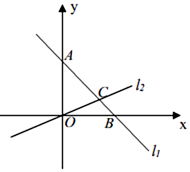 (1)、求点C的坐标;(2)、若平行于y轴的直线 交于直线 于点E,交直线 于点D,交x轴于点M,且 ,求a的值;17. 已知:一次函数y=3x﹣5与y=2x+b的图象的交点的坐标为P(1,﹣2).
(1)、求点C的坐标;(2)、若平行于y轴的直线 交于直线 于点E,交直线 于点D,交x轴于点M,且 ,求a的值;17. 已知:一次函数y=3x﹣5与y=2x+b的图象的交点的坐标为P(1,﹣2).求:方程组 的解和b的值.
18. 已知一次函数y=kx+2与y=x﹣1的图象相交,交点的横坐标为2.(1)求k的值;
(2)直接写出二元一次方程组 的解.
19. 若正比例函数y=﹣x的图象与一次函数y=x+m的图象交于点A,且点A的横坐标为﹣1.(1)求该一次函数的解析式;
(2)直接写出方程组 的解.
四、综合题
-
20. 如图, , 分别表示两个一次函数的图象,它们相交于点P.
 (1)、求出两条直线的函数关系式(2)、点P的坐标可看作是哪个二元一次方程组的解.21. 习近平总书记说:“人民群众多读书,我们的民族精神就会厚重起来、深邃起来.”某书店计划在4月23日世界读书日之前,同时购进A,B两类图书,已知购进3本A类图书和4本B类图书共需288元;购进6本A类图书和2本B类图书共需306元.(1)、A,B两类图书每本的进价各是多少元?(2)、该书店计划用4500元全部购进两类图书,设购进A类x本,B类y本.
(1)、求出两条直线的函数关系式(2)、点P的坐标可看作是哪个二元一次方程组的解.21. 习近平总书记说:“人民群众多读书,我们的民族精神就会厚重起来、深邃起来.”某书店计划在4月23日世界读书日之前,同时购进A,B两类图书,已知购进3本A类图书和4本B类图书共需288元;购进6本A类图书和2本B类图书共需306元.(1)、A,B两类图书每本的进价各是多少元?(2)、该书店计划用4500元全部购进两类图书,设购进A类x本,B类y本.①求y关于x的关系式;
②进货时,A类图书的购进数量不少于60本,已知A类图书每本的售价为38元,B类图书每本的售价为50元,求如何进货才能使书店所获利润最大,最大利润为多少元?
