湖北省咸宁市通城县2023-2024学年九年级上学期开学考试数学试题
试卷更新日期:2023-10-07 类型:开学考试
一、单选题
-
1. 下列各式:①;②;③;④;⑤ , 其中二次根式有( )A、1个 B、2个 C、3个 D、4个2. 下列各组数据中的三个数,可作为三边长构成直角三角形的是( )A、4,5,6 B、2,3,4 C、11,12,13 D、8,15,173. 下列给出的条件中,能判断四边形是平行四边形的是( )A、 , B、 , C、 , D、 ,4. 已知一次函数 , 点在该函数图象上,则a与b的大小关系是( ).A、 B、 C、 D、5. 若一个菱形的两条对角线长分别是5cm和10cm,则与该菱形面积相等的正方形的边长是( )A、6cm B、5cm C、cm D、7.5cm6. 如图,正方形是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接 , , 则( )
 A、 B、 C、 D、7. 已知直线y=kx+8与x轴和y轴所围成的三角形的面积是4,则k的值是( )A、-8 B、8 C、±8 D、48. 如图,一次函数与正比例函数(m,n为常数,且)的图象是( )A、
A、 B、 C、 D、7. 已知直线y=kx+8与x轴和y轴所围成的三角形的面积是4,则k的值是( )A、-8 B、8 C、±8 D、48. 如图,一次函数与正比例函数(m,n为常数,且)的图象是( )A、 B、
B、 C、
C、 D、
D、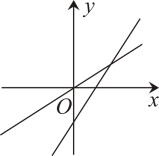
二、填空题
-
9. 计算: =
10. 若y=是正比例函数,则m=11. 如图,中,的平分线交于 , 则 . 12. 如图,直线过正方形ABCD的顶点B,点A、C到直E的距离分别是1和2,则正方形ABCD面积是.
12. 如图,直线过正方形ABCD的顶点B,点A、C到直E的距离分别是1和2,则正方形ABCD面积是.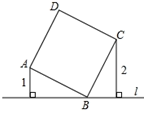 13. 如图,在平行四边形ABCD中,AC⊥BC,E为AB的中点,若CE=5,AC=8,则AD= .
13. 如图,在平行四边形ABCD中,AC⊥BC,E为AB的中点,若CE=5,AC=8,则AD= . 14. 若数2,3,x,5,6五个数的平均数为4,则x的值为 .
14. 若数2,3,x,5,6五个数的平均数为4,则x的值为 .
15.如图:函数y=2x和y=ax+4的图象交于点A(m,2),不等式2x<ax+4的解集为 .
 16. 已知a,b,c为三角形三边,则 = .
16. 已知a,b,c为三角形三边,则 = .三、解答题
-
17. 计算:(1)、;(2)、 .18. 下表是某校八年级(1)班20名学生某次数学测验的成绩统计表
成绩(分)
60
70
80
90
100
人数(人)
1
5
x
y
2
(1)、若这20名学生成绩的平均分数为82分,求x和y的值;(2)、在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求 的值.19. 一次函数图象经过和两点.(1)、求这个一次函数的解析式;(2)、当时,求的值.20. 已知,直线y=2x+3与直线y=-2x-1. (1)、求两直线与y轴交点A,B的坐标;(2)、求两直线交点C的坐标;(3)、求△ABC的面积.21. 如图,直线与轴,轴分别交于两点,点的坐标为 .
(1)、求两直线与y轴交点A,B的坐标;(2)、求两直线交点C的坐标;(3)、求△ABC的面积.21. 如图,直线与轴,轴分别交于两点,点的坐标为 . (1)、求的值;(2)、若点是直线在第一象限内的动点 , 试确定点的坐标,使的面积为12.22. 如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?
(1)、求的值;(2)、若点是直线在第一象限内的动点 , 试确定点的坐标,使的面积为12.22. 如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长? 23.
23.如图,四边形ABCD中,AB∥CD , AC平分∠BAD , CE∥AD交AB于E .
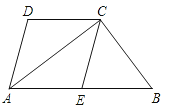 (1)、求证:四边形AECD是菱形;(2)、若点E是AB的中点,试判断△ABC的形状,并说明理由.24. 我市某化工厂现有甲种原料290kg,乙种原料212kg,计划利用这两种原料生产A,B两种产品共80件.生产一件A产品需要甲种原料5kg,乙种原料1.5kg,生产成本是120元;生产一件B产品,需要甲种原料2.5kg,乙种原料3.5kg,生产成本是200元.(1)、该化工厂现有的原料能否保证生产?若能的话,有几种生产方案,请你设计出来;(2)、设生产A,B两种产品的总成本为y元,设A种的生产件数为x,试写出y与x之间的函数关系,并利用函数的性质说明(1)中哪种生产方案总成本最低?最低生产总成本是多少?25. 如图,在中, , 过点C的直线 , D为边上一点,过点D作 , 交直线于E,垂足为F,连接、 .
(1)、求证:四边形AECD是菱形;(2)、若点E是AB的中点,试判断△ABC的形状,并说明理由.24. 我市某化工厂现有甲种原料290kg,乙种原料212kg,计划利用这两种原料生产A,B两种产品共80件.生产一件A产品需要甲种原料5kg,乙种原料1.5kg,生产成本是120元;生产一件B产品,需要甲种原料2.5kg,乙种原料3.5kg,生产成本是200元.(1)、该化工厂现有的原料能否保证生产?若能的话,有几种生产方案,请你设计出来;(2)、设生产A,B两种产品的总成本为y元,设A种的生产件数为x,试写出y与x之间的函数关系,并利用函数的性质说明(1)中哪种生产方案总成本最低?最低生产总成本是多少?25. 如图,在中, , 过点C的直线 , D为边上一点,过点D作 , 交直线于E,垂足为F,连接、 .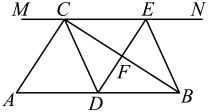 (1)、求证:;(2)、当D在中点时,四边形是什么特殊四边形?请说明你的理由;(3)、若D为中点,则当的大小满足什么条件时,四边形是正方形?请说明你的理由.
(1)、求证:;(2)、当D在中点时,四边形是什么特殊四边形?请说明你的理由;(3)、若D为中点,则当的大小满足什么条件时,四边形是正方形?请说明你的理由.