江苏省苏州市高新区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-10-07 类型:期末考试
一、单选题
-
1. 若a≠b,则下列分式变形正确的是( )A、 B、 C、 D、2. 某校为了解八年级300名学生每周课外阅读时间,从八年级6个班级中共抽取50名学生作调查,下列说法正确的是( )A、该校300名八年级学生是总体 B、抽取的50名学生是总体的一个样本 C、每个八年级学生每周课外阅读时间是个体 D、样本容量是603. 袋子里有8个红球,m个白球,3个黑球,每个球除颜色外都相同,从中任意摸出一个球,若摸到红球的可能性最大,则m的值不可能是( )A、1 B、3 C、5 D、104. 正比例函数y=2x和反比例函数 的一个交点为(1,2),则另一个交点为( )A、(﹣1,﹣2) B、(﹣2,﹣1) C、(1,2) D、(2,1)5. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm , 接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
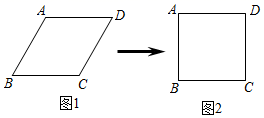 A、20cm B、30cm C、40cm D、20 cm6. 如图,两个反比例函数和在第一象限内的图象分别是和 , 设点P在上,轴于点A,交于点B,已知的面积为4,则k的值为( )
A、20cm B、30cm C、40cm D、20 cm6. 如图,两个反比例函数和在第一象限内的图象分别是和 , 设点P在上,轴于点A,交于点B,已知的面积为4,则k的值为( ) A、16 B、14 C、12 D、107. 如图,四边形是菱形,按以下步骤作图:①以顶点B为圆心,长为半径作弧,交于点E;②分别以D、E为圆心,以大于的长为半径作弧,两弧相交于点F,作射线交于点G,连接 , 若 , , 则菱形的面积为( )
A、16 B、14 C、12 D、107. 如图,四边形是菱形,按以下步骤作图:①以顶点B为圆心,长为半径作弧,交于点E;②分别以D、E为圆心,以大于的长为半径作弧,两弧相交于点F,作射线交于点G,连接 , 若 , , 则菱形的面积为( )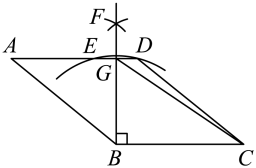 A、16 B、 C、 D、128. 如图(1),在平面直角坐标系中,矩形在第一象限,且轴,直线沿x轴正方向平移,在平移过程中,直线被矩形截得的线段长为a,直线在x轴上平移的距离为b,a、b间的函数关系图象如图(2)所示,那么矩形的面积为( )
A、16 B、 C、 D、128. 如图(1),在平面直角坐标系中,矩形在第一象限,且轴,直线沿x轴正方向平移,在平移过程中,直线被矩形截得的线段长为a,直线在x轴上平移的距离为b,a、b间的函数关系图象如图(2)所示,那么矩形的面积为( )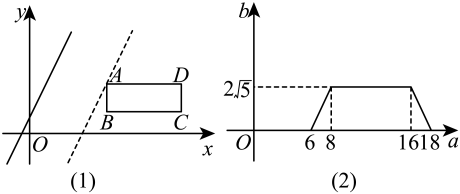 A、20 B、 C、40 D、32
A、20 B、 C、40 D、32二、填空题
-
9. 一组数据共50个,若第5组的频率为 , 则第5组的频数为 .10. 若关于x的方程是一元二次方程,则a的取值范围是 .11. 已知AB=2,点C是线段AB的黄金分割点(AC>BC),则AC=.12. 已知一次函数与反比例函数相交于点 , , 不等式的解集是 .13. 如图,的对角线相交于点O, , , , 则的周长为cm.
 14. 如图,四边形中, , 且与不平行,P、M、N分别是、、的中点,则的范围是 .
14. 如图,四边形中, , 且与不平行,P、M、N分别是、、的中点,则的范围是 .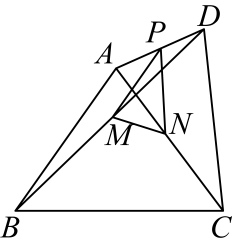 15. 关于的方程的解为非负数,则的取值范围是 .16. 数学兴趣小组的同学拿出如图所示的矩形纸片 , 其中 , 他们将纸片对折使、重合,展开后得折痕 , 又沿折叠使点C落在处,展开后又得到折痕 , 再沿折叠使点A落在上的处,大家发现了很多有趣的结论.就这个图形,请你探究的值为 .
15. 关于的方程的解为非负数,则的取值范围是 .16. 数学兴趣小组的同学拿出如图所示的矩形纸片 , 其中 , 他们将纸片对折使、重合,展开后得折痕 , 又沿折叠使点C落在处,展开后又得到折痕 , 再沿折叠使点A落在上的处,大家发现了很多有趣的结论.就这个图形,请你探究的值为 .
三、解答题
-
17. 解方程: .18. 计算:19. 我校为落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人必选且只选一类最喜欢的课程),将调查结果绘制成如图所示的两幅不完整的统计图.
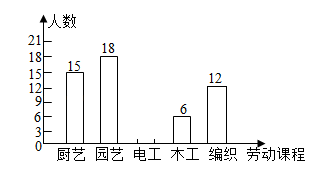
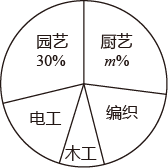
请根据统计图提供的信息,解答下列问题
(1)、本次随机调查的学生人数为人;(2)、补全条形统计图;(3)、扇形统计图中m的值为 ;(4)、若该校七年级共有名学生,请估计我校七年级学生选择“编织”劳动课的人数.20. 在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率
0.420
0.410
0.412
0.406
0.403
b
(1)、按表格数据格式,表中的a=;b=;(2)、请估计:当次数s很大时,摸到白球的频率将会接近(精确到0.1);(3)、请推算:摸到红球的概率是(精确到0.1);(4)、试估算:这一个不透明的口袋中红球有只.21. 甲、乙两公司为某基金会各捐款30 000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐20元.甲、乙两公司各有多少人?22. 如图,在平面直角坐标系中,点A的坐标为 , 点B的坐标为 .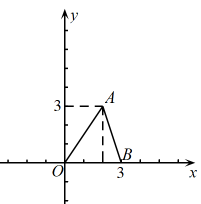 (1)、把沿x轴向左平移1个单位长度得到 , 直接写出的坐标为;(2)、把绕原点旋转得到 , 直接写出点的坐标为;(3)、把沿x轴翻折得到 , 直接写出点的坐标为;(4)、以点O为位似中心,在第一象限内把按相似比放大,得到 , 画出 , 并写出点的坐标为 ▲ .23. 如图,在平面直角坐标系中,反比例函数的图象如图所示,矩形在第一象限内,平行于x轴,且 , 点A的坐标为
(1)、把沿x轴向左平移1个单位长度得到 , 直接写出的坐标为;(2)、把绕原点旋转得到 , 直接写出点的坐标为;(3)、把沿x轴翻折得到 , 直接写出点的坐标为;(4)、以点O为位似中心,在第一象限内把按相似比放大,得到 , 画出 , 并写出点的坐标为 ▲ .23. 如图,在平面直角坐标系中,反比例函数的图象如图所示,矩形在第一象限内,平行于x轴,且 , 点A的坐标为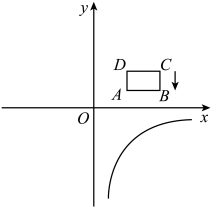 (1)、直接写出B,C,D三点的坐标;(2)、若将矩形向下平移m个单位,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点?并求m的值和反比例函数的表达式.24. 如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
(1)、直接写出B,C,D三点的坐标;(2)、若将矩形向下平移m个单位,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点?并求m的值和反比例函数的表达式.24. 如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?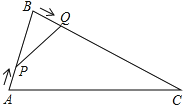 25. 如图,在正方形中,点E是边的中点,将沿翻折得到 . 延长交于点H,连接 .
25. 如图,在正方形中,点E是边的中点,将沿翻折得到 . 延长交于点H,连接 .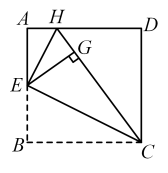 (1)、求证:;(2)、若 , 求的长.26. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于B,与x轴交于A,与y轴交于C.
(1)、求证:;(2)、若 , 求的长.26. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于B,与x轴交于A,与y轴交于C.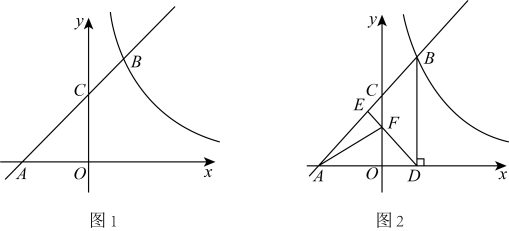 (1)、若点 .
(1)、若点 .①求一次函数和反比例函数的解析式;
②在y轴上取一点P,当的面积为5时,求点P的坐标;
(2)、过点B作轴于点D,点E为中点,线段交y轴于点F,连接 . 若的面积为11,求k的值.27. 如图 (1)、如图1,四边形是正方形,点E是边上的一个动点,以为边在的右侧作正方形 , 连接 , , 则与的数量关系是 .(2)、如图2,四边形是矩形, , , 点E是边上的一个动点,以为边在的右侧作矩形 , 且 , 连接 , . 判断线段与 , 有怎样的数量关系和位置关系,并说明理由;(3)、如图3,在(2)的条件下,点E是从点A运动D点,则点G的运动路径长度为;(4)、如图3,在(2)的条件下,连接BG,则的最小值为 .
(1)、如图1,四边形是正方形,点E是边上的一个动点,以为边在的右侧作正方形 , 连接 , , 则与的数量关系是 .(2)、如图2,四边形是矩形, , , 点E是边上的一个动点,以为边在的右侧作矩形 , 且 , 连接 , . 判断线段与 , 有怎样的数量关系和位置关系,并说明理由;(3)、如图3,在(2)的条件下,点E是从点A运动D点,则点G的运动路径长度为;(4)、如图3,在(2)的条件下,连接BG,则的最小值为 .