江苏省苏州市吴江区2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-10-07 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 近年来,中国北斗芯片实现了22纳米制程的突破,领先GPS芯片. 已知22纳米=米,数据0.000000022用科学记数法可表示为( )A、 B、 C、 D、3. 线段a,b,c首尾顺次相接组成三角形,若 , , 则c的长度可以是( )A、2 B、3 C、4 D、84. 若 , 下列不等式一定成立的是( )A、 B、 C、 D、5. 已知 , , 则的值是( )A、 B、 C、 D、6. 如图,点E在BC的延长线上,下列条件中不能判定的是( )
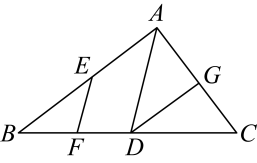
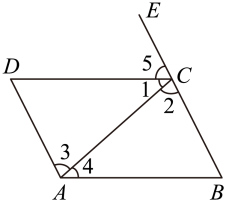 A、 B、 C、 D、7. 被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.书中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”原文大意为:“现在有5只雀、6只燕,分别集中放在天平上称重,聚在一起的雀重燕轻.将一只雀一只燕交换位置而放,重量相等,5只雀和6只燕共重1斤,问雀和燕各重多少?”设雀每只斤,燕每只斤,则可列出方程组为( )A、 B、 C、 D、8. 如图,是的中线,过点D作 , 交于点E,是的角平分线,点M在边上,且 , 点N在线段上,若 , 记的面积为 , 的面积为 , 则的值为( )
A、 B、 C、 D、7. 被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.书中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”原文大意为:“现在有5只雀、6只燕,分别集中放在天平上称重,聚在一起的雀重燕轻.将一只雀一只燕交换位置而放,重量相等,5只雀和6只燕共重1斤,问雀和燕各重多少?”设雀每只斤,燕每只斤,则可列出方程组为( )A、 B、 C、 D、8. 如图,是的中线,过点D作 , 交于点E,是的角平分线,点M在边上,且 , 点N在线段上,若 , 记的面积为 , 的面积为 , 则的值为( )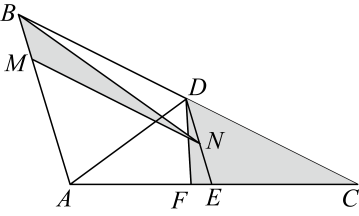 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
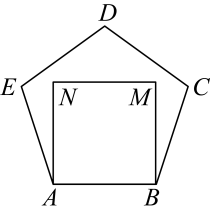
9. .10. 已知是方程的解,则 .11. 若 , , 则 .12. 命题“对顶角相等”的逆命题是13. 如图,以为一边在正五边形内作正方形 , 则度.
 14. 如图,将矩形纸片沿折叠后,点D、C分别落在点、的位置,的延长线交于点G,若 , 则度.
14. 如图,将矩形纸片沿折叠后,点D、C分别落在点、的位置,的延长线交于点G,若 , 则度.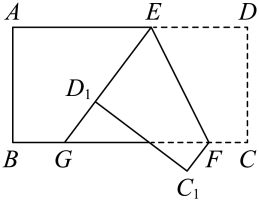 15. 定义:如果三角形的一个内角是另一个内角的2倍,那么称这个三角形为“倍角三角形”.若是“倍角三角形”, , , 则度.16. 如图,已知长方形中, , , 点在边上, , 点在线段上以的速度由点向点运动,到达点后马上折返,向点运动,点在线段上以的速度由C点向D点运动.点F、G同时出发,当一个点到达终点停止运动时,另一个点也随之停止运动,设运动的时间为t秒.若以E,B,F为顶点的三角形和以F,C,G为顶点的三角形全等,则t=秒.
15. 定义:如果三角形的一个内角是另一个内角的2倍,那么称这个三角形为“倍角三角形”.若是“倍角三角形”, , , 则度.16. 如图,已知长方形中, , , 点在边上, , 点在线段上以的速度由点向点运动,到达点后马上折返,向点运动,点在线段上以的速度由C点向D点运动.点F、G同时出发,当一个点到达终点停止运动时,另一个点也随之停止运动,设运动的时间为t秒.若以E,B,F为顶点的三角形和以F,C,G为顶点的三角形全等,则t=秒.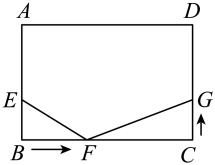
三、解答题
-
17. 计算:(1)、;(2)、 .18. 因式分解:(1)、;(2)、 .19. 先化简再求值 , 其中 .20.(1)、解方程组;(2)、解不等式组 .21. 如图, , . 与相等吗?为什么?
 22. 如图,在中,O为的中点, , 直线交于点E.
22. 如图,在中,O为的中点, , 直线交于点E.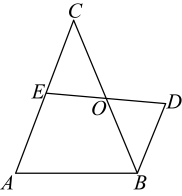 (1)、求证:;(2)、若 , 求的长.23. 如图,点是的一边上一点.请利用无刻度直尺和圆规作图,保留作图痕迹,不写作法.
(1)、求证:;(2)、若 , 求的长.23. 如图,点是的一边上一点.请利用无刻度直尺和圆规作图,保留作图痕迹,不写作法.
⑴在的内部求作射线 , 使得;
⑵求作直线 , 使得 , 交射线于点;
⑶求作直线 , 使得 于点 .
24. 为振兴乡村经济,弘扬“四敢”精神,某村拟建A,B两类展位供当地的农产品展览和销售.1个A类展位的占地面积比1个B类展位的占地面积多4平方米;10个A类展位和5个B类展位的占地面积共 280 平方米.建A类展位每平方米的费用为120元,建B类展位每平方米的费用为100元.(1)、求每个A,B类展位占地面积各为多少平方米?(2)、该村拟建A,B两类展位共40个,B类展位的数量小于A类展位数量的2倍,且建造这40个展位的总费用不超过77000元,求该村共有哪些建设方案?25. 阅读下列材料:我们把多项式及叫做完全平方公式,如果一个多项式不是完全平方公式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,可以求代数式的最大值或最小值.
例如:求代数式的最小值.
, 可知当时,有最小值,最小值是 .
再例如:求代数式的最大值.
, 可知当时,有最大值,最大值是 .
(1)、【直接应用】代数式的最小值为;(2)、【类比应用】若多项式 , 试求的最小值;(3)、【知识迁移】如图,学校打算用长米的篱笆围一个长方形的菜地,菜地的一面靠墙(墙足够长),求围成的菜地的最大面积. 26. 已知 , , 点P是射线上的一个动点.
26. 已知 , , 点P是射线上的一个动点.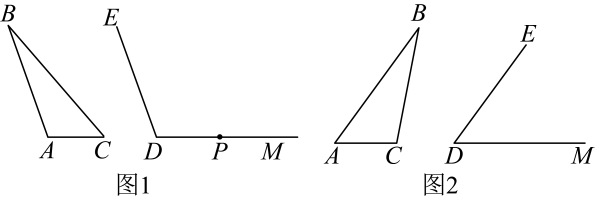 (1)、如图1,连接 , 若 , , 求证:;(2)、如图1,连接 , 若 , , 则是否成立,若成立,写出证明过程,若不成立,请说明理由;(3)、如图2,连接 , 若 , , , 射线平分 , 射线平分 , 射线与射线相交于点Q,则的度数为 .27. 定义:关于 , 的二元一次方程(其中)中的常数项与未知数系数 , 之一互换,得到的方程叫“交换系数方程”,例如:的交换系数方程为或 .(1)、方程与它的“交换系数方程”组成的方程组的解为;(2)、已知关于 , 的二元一次方程的系数满足 , 且与它的“交换系数方程”组成的方程组的解恰好是关于 , 的二元一次方程的一个解,求代数式的值;(3)、已知整数 , , 满足条件 , 并且是关于 , 的二元一次方程的“交换系数方程”求的值.
(1)、如图1,连接 , 若 , , 求证:;(2)、如图1,连接 , 若 , , 则是否成立,若成立,写出证明过程,若不成立,请说明理由;(3)、如图2,连接 , 若 , , , 射线平分 , 射线平分 , 射线与射线相交于点Q,则的度数为 .27. 定义:关于 , 的二元一次方程(其中)中的常数项与未知数系数 , 之一互换,得到的方程叫“交换系数方程”,例如:的交换系数方程为或 .(1)、方程与它的“交换系数方程”组成的方程组的解为;(2)、已知关于 , 的二元一次方程的系数满足 , 且与它的“交换系数方程”组成的方程组的解恰好是关于 , 的二元一次方程的一个解,求代数式的值;(3)、已知整数 , , 满足条件 , 并且是关于 , 的二元一次方程的“交换系数方程”求的值.