湖北省武汉市青山区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-10-07 类型:期末考试
一、单选题
-
1. 若代数式在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、2. 下列函数中,y是x的正比例函数的是( )A、 B、 C、 D、3. 以下列各组数为边长,能构成直角三角形的是( )A、1,2,3 B、2,3,4 C、2,2,5 D、2, , 34. 某校组织环保知识竞赛,为参加区级比赛做选手选拔工作,经过多次测试后,有4名同学成为区级参赛选手的候选人,具体情况如下表:
甲
乙
丙
丁
平均分
90
92
95
95
方差
36
32
21
33
如果从这4名同学中选出1位参加区级比赛(总体水平高且状态稳定),你会推荐( )
A、甲 B、乙 C、丙 D、丁5. 如图,在矩形中,对角线 , 相交于点 . 下列结论中不一定成立的是( )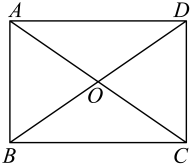 A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 已知一次函数 , 那么下列结论正确的是( )A、y的值随x的值增大而增大 B、图象经过第一、二、三象限 C、图象必经过点 D、当时,8. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )
A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 已知一次函数 , 那么下列结论正确的是( )A、y的值随x的值增大而增大 B、图象经过第一、二、三象限 C、图象必经过点 D、当时,8. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )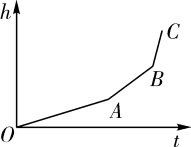 A、
A、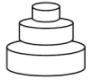 B、
B、 C、
C、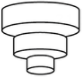 D、
D、 9. 如图,在矩形纸片中, , 将其折叠,使点与点重合,折痕为 , 设与交于点 , 连接 . 若 , 则的长为( )
9. 如图,在矩形纸片中, , 将其折叠,使点与点重合,折痕为 , 设与交于点 , 连接 . 若 , 则的长为( )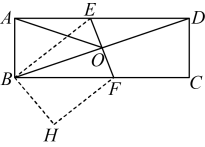 A、 B、 C、 D、10. 如图,已知点 , 点M,N分别是直线和直线上的动点,连接 , . 的最小值为( )
A、 B、 C、 D、10. 如图,已知点 , 点M,N分别是直线和直线上的动点,连接 , . 的最小值为( )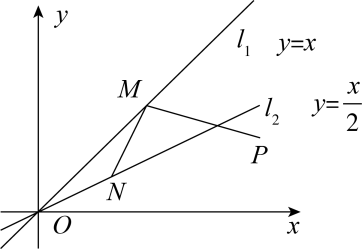 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
11. 计算:( )2=。12. 一列火车以的速度匀速前进.则它的行驶路程s(单位:)关于行驶时间t(单位:)的函数解析式为 .13. 小明参加“建团百年,我为团旗添光彩”主题演进比赛,其演讲形象、内容、效果三项得分分别是9分,8分,8分.若将三项得分依次按3∶4∶3的比例确定最终成绩,则小明的最终比赛成绩为分.14. 如图,在正方形的外侧,作等边三角形 , 连接 , . 则 .
 15. 已知直线过点﹒则以下结论:①;②若当时, , 则;③方程组的解为;④若直线向右平移2个单位后过点 , 且不等式的解集为 , 则 , 其中正确的有 . (请填写序号)16. 如图, , , , 点是的中点,且 , 则 .
15. 已知直线过点﹒则以下结论:①;②若当时, , 则;③方程组的解为;④若直线向右平移2个单位后过点 , 且不等式的解集为 , 则 , 其中正确的有 . (请填写序号)16. 如图, , , , 点是的中点,且 , 则 .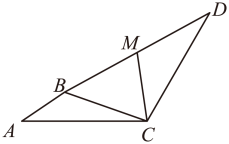
三、解答题
-
17. 计算:(1)、;(2)、 .18. 物理实验证实:在弹性限度内,某弹簧长度()与所挂物体质量()满足函数关系 . 表格是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
0
2
5
15
19
25
(1)、求与的函数关系式;(2)、当弹簧长度为21cm时,求所挂物体的质量.19. 某中学为了解本校八年级学生参加志愿者活动的次数,随机调查了该年级20名学生,统计得到该20名学生参加志愿者活动的次数如下:3,5,3,6,3,4,4,5,2,4,5,6,1,3,5,5,4,4,2,4.根据以上数据,得到如下不完整的频数分布表:次数
1
2
3
4
5
6
人数
1
2
6
2
(1)、表格中的 , ;(2)、在这次调查中,参加志愿者活动次数的众数为 , 中位数为;(3)、若该校八年级共有600名学生,根据调查统计结果,估计该校八年级学生参加志愿者活动的次数不低于4次的人数.20. 如图,的对角线 , 相交于点O,且 , , .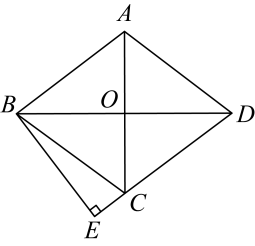 (1)、求证:为菱形;(2)、过点B作于点E.求的长.21. 如图,是由小正方形组成的网格,每个小正方形的顶点叫做格点,的三个顶点都是格点,点是上一点,仅用无刻度的直尺在给定网格中完成画图.(画图过程用虚线表示,画图结果用实线表示).
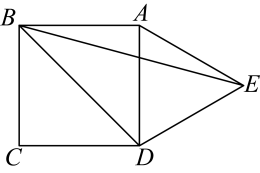
(1)、求证:为菱形;(2)、过点B作于点E.求的长.21. 如图,是由小正方形组成的网格,每个小正方形的顶点叫做格点,的三个顶点都是格点,点是上一点,仅用无刻度的直尺在给定网格中完成画图.(画图过程用虚线表示,画图结果用实线表示). (1)、在图(1)中,以为边画平行四边形 , 再将线段平移到 , 使点与点对应,点与点对应,画出线段;(2)、在图(2)中,过点画 , 且 , 再在上找点 , 使 .22. 某公司计划购买两种设备共100台,要求种设备数量不低于种的 , 且不高于种的 . 已知两种设备的单价分别是1000元/台,1500元/台,设购买种设备台.(1)、求该公司计划购买这两种设备所需费用(元)与的函数关系式;(2)、求该公司按计划购买这两种设备有多少种方案?(3)、由于市场行情波动,实际购买时,种设备单价上调了元/台,种设备单价下调了元/台,此时公司购买这两种设备所需最少费用为121500元,请直接写出的值.23. 已知,点E是的中线上一动点,交于点F,连接 .
(1)、在图(1)中,以为边画平行四边形 , 再将线段平移到 , 使点与点对应,点与点对应,画出线段;(2)、在图(2)中,过点画 , 且 , 再在上找点 , 使 .22. 某公司计划购买两种设备共100台,要求种设备数量不低于种的 , 且不高于种的 . 已知两种设备的单价分别是1000元/台,1500元/台,设购买种设备台.(1)、求该公司计划购买这两种设备所需费用(元)与的函数关系式;(2)、求该公司按计划购买这两种设备有多少种方案?(3)、由于市场行情波动,实际购买时,种设备单价上调了元/台,种设备单价下调了元/台,此时公司购买这两种设备所需最少费用为121500元,请直接写出的值.23. 已知,点E是的中线上一动点,交于点F,连接 . (1)、如图1,当点E与点D重合时,求证:;(2)、如图2,当点E与点D不重合时,延长交于点G,交于点H.
(1)、如图1,当点E与点D重合时,求证:;(2)、如图2,当点E与点D不重合时,延长交于点G,交于点H.①判断四边形的形状,并说明理由;
②如图3,若的边 , 以为腰作等腰直角 , 连接 , 点M为的中点,当点E从点D运动到点A过程中,请直接写出点M的运动路径长.
24. 如图,在平面直角坐标系中,直线分别与轴,轴交于两点,以线段为边,在第一象限内作正方形 , 直线与轴交于点 , 与线段交于点 , 且 .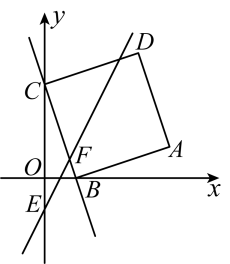 (1)、已知 .
(1)、已知 .①请直接写出点和点的坐标;
②若 , 求点的坐标;
(2)、若 , 请直接写出与的数量关系.