2023年浙教版数学八年级上册第五章 一次函数 单元测试(B卷)
试卷更新日期:2023-10-03 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 弹簧挂重物会伸长,测得弹簧长度y(cm)最长为20cm,与所挂物体重量x(kg)有下面的关系.
x
0
1
2
3
4
…
y
8
8.5
9
9.5
10
…
下列说法不正确的是( )
A、x与y都是变量,x是自变量,y是因变量 B、所挂物体为6kg,弹簧长度为11cm C、物体每增加1kg,弹簧长度就增加0.5cm D、挂30kg物体时一定比原长增加15cm2. 下列各列表中,不能表示y是x的函数的是( )A、
B、x 1 2 3 4 5 y 6 7 8 9 1
C、x 1 2 3 4 5 y 8 8 8 8 10
D、x 1 2 2 4 5 y 6 3 2 1 5 x 1 2 3 4 5 y 2 4 6 8 10 3. 在直角三角形ABC中, , , , 则y与x之间的函数关系式是( )A、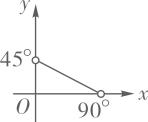 B、
B、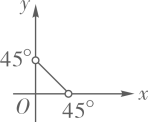 C、
C、 D、
D、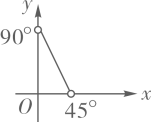 4. 瓶子或者罐头盒等圆柱形的物体常常如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如表,则下列说法错误的是( )
4. 瓶子或者罐头盒等圆柱形的物体常常如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如表,则下列说法错误的是( )层数n/层
1
2
3
4
5
……
物体总数y/个
1
3
6
10
15
……
 A、在这个变化过程中层数是自变量,物体总数是因变量 B、当堆放层数为7层时,物体总数为28个 C、物体的总数随着层数的增加而均匀增加 D、物体的总数y与层数n之间的关系式为5. 在同一直角坐标系内作一次函数和图象,可能是( )A、
A、在这个变化过程中层数是自变量,物体总数是因变量 B、当堆放层数为7层时,物体总数为28个 C、物体的总数随着层数的增加而均匀增加 D、物体的总数y与层数n之间的关系式为5. 在同一直角坐标系内作一次函数和图象,可能是( )A、 B、
B、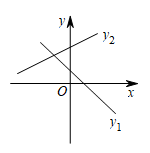 C、
C、 D、
D、 6. 已知函数是y关于x的一次函数,则m的取值范围是( )A、 B、 C、 D、m为任意实数7. 小凡遇到了这样一道题目:选择适当的x值,并求代数式的值.他将同学们的答案进行了如下整理,并有3个大胆的猜测:
6. 已知函数是y关于x的一次函数,则m的取值范围是( )A、 B、 C、 D、m为任意实数7. 小凡遇到了这样一道题目:选择适当的x值,并求代数式的值.他将同学们的答案进行了如下整理,并有3个大胆的猜测:x
1
2
3
4
5
…
2
…
①当时,代数式的值随着x的增大而越来越小;
②代数式的值有可能等于1;
③当时,代数式的值随着x的减小而越来越接近于1.
推测正确的有( )
A、0个 B、1个 C、2个 D、3个8. A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:
①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;②甲出发4h后被乙追上;③甲比乙晚到;④甲车行驶8h或 , 甲,乙两车相距80km;
其中错误的( )
A、序号① B、序号② C、序号③ D、序号④9. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,直线与x轴交于点C,与y轴交于点B,若线段上的点D到直线的距离长为3,则点D的坐标为( ) A、 B、 C、 D、10. 如图,直线与x轴交于点B,与y轴交于点C,点 , D为线段的中点,P为y轴上的一个动点,连接、 , 当的周长最小时,点P的坐标为( )
A、 B、 C、 D、10. 如图,直线与x轴交于点B,与y轴交于点C,点 , D为线段的中点,P为y轴上的一个动点,连接、 , 当的周长最小时,点P的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 等腰三角形的周长是10厘米,腰长是厘米,底边长是厘米,请写出关于的函数关系式,并写出自变量的取值范围 .12. 在直角坐标系中,有A(3,﹣3),B(5,3)两点,现另取一点C(1,n),当△ABC周长最小时,n的值是 .13. 已知过点的直线不经过第一象限.s=a+2b,则s的取值范围是.14. 如图,某链条每节长为 , 每两节链条相连接部分重叠的圆的直径为 , 按这种连接方式,x节链条总长度为 , 则y关于x的函数关系式是.
 15. 设直线 : 和直线 : ( 是正整数)及 轴围成的三角形面积是 ,当 时,直线 : 和直线 : ,这两条直线与 轴围成的面积记为 ,则 .16. 如图,在平面直角坐标系中,一次函数y=-2x+4的图象与x轴、y轴分别交于点A和点B , 过点B的直线BC:y=kx+b交x轴于点C(-8,0).
15. 设直线 : 和直线 : ( 是正整数)及 轴围成的三角形面积是 ,当 时,直线 : 和直线 : ,这两条直线与 轴围成的面积记为 ,则 .16. 如图,在平面直角坐标系中,一次函数y=-2x+4的图象与x轴、y轴分别交于点A和点B , 过点B的直线BC:y=kx+b交x轴于点C(-8,0). (1)、k的值为;(2)、点M为直线BC上一点,若∠MAB=∠ABO , 则点M的坐标是.
(1)、k的值为;(2)、点M为直线BC上一点,若∠MAB=∠ABO , 则点M的坐标是.三、解答题(共8题,共66分)
-
17. 如图,图中的小方格都是边长为1的正方形,
 (1)、画出△ABC关于y轴的对称图形△A1B1C1 , 并直接写出△A1B1C1的各顶点坐标:(2)、P为x轴上一动点,连接PB,PC,当PB+PC的值最小时,请在图中作出点P,(保留作图痕迹)并直接写出点P的坐标为( ).18. 如图,在平面直角坐标系中,函数的图象与x轴,y轴分别交于点A,B,与函数的图象交于点 .
(1)、画出△ABC关于y轴的对称图形△A1B1C1 , 并直接写出△A1B1C1的各顶点坐标:(2)、P为x轴上一动点,连接PB,PC,当PB+PC的值最小时,请在图中作出点P,(保留作图痕迹)并直接写出点P的坐标为( ).18. 如图,在平面直角坐标系中,函数的图象与x轴,y轴分别交于点A,B,与函数的图象交于点 . (1)、求m和b的值;(2)、函数的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速向x轴正方向运动.设点E的运动时间为t秒.当的面积为12时,求t的值;19. 已知,一次函数y=x+4的图象与x轴、y轴分别交于点A , 点B , 点C的坐标为(-2,0).
(1)、求m和b的值;(2)、函数的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速向x轴正方向运动.设点E的运动时间为t秒.当的面积为12时,求t的值;19. 已知,一次函数y=x+4的图象与x轴、y轴分别交于点A , 点B , 点C的坐标为(-2,0). (1)、求点A , 点B的坐标;(2)、过点C作直线CD , 与AB交于点D , 且 , 求点D的坐标;(3)、连接BC , 将△OBC沿x轴向左平移得到△O′B′C′ , 再将以A , B , B′ , C′为顶点的四边形沿O′B′剪开得到两个图形.若用这两个图形拼成不重叠且无缝隙的图形恰好是三角形,求△OBC平移的距离.20. 如图,在平面直角坐标系中,直线y= 与 轴交于点 ,与 轴交于点 ,已知点 .
(1)、求点A , 点B的坐标;(2)、过点C作直线CD , 与AB交于点D , 且 , 求点D的坐标;(3)、连接BC , 将△OBC沿x轴向左平移得到△O′B′C′ , 再将以A , B , B′ , C′为顶点的四边形沿O′B′剪开得到两个图形.若用这两个图形拼成不重叠且无缝隙的图形恰好是三角形,求△OBC平移的距离.20. 如图,在平面直角坐标系中,直线y= 与 轴交于点 ,与 轴交于点 ,已知点 .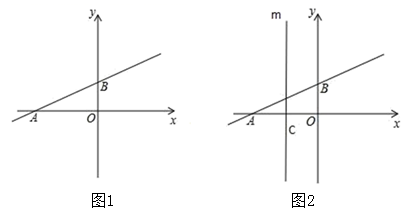 (1)、求出点 ,点 的坐标.(2)、 是直线 上一动点,且 和 的面积相等,求点 坐标.(3)、如图2,平移直线 l ,分别交 x 轴, y轴于交于点 A , B ,过点 C 作平行于 y 轴的直线m ,在直线 m 上是否存在点 Q ,使得 △ABQ 是等腰直角三角形?若存在,请直接写出所有符合条件的点 Q 的坐标.21. 12月,浙江突发疫情,我市立即启动疫情应急处置模拟演练.为配合演练顺利开展,某校需要购进A、B两款体温枪共100只.已知购进A型体温枪花费1000元,B型体温枪花费1500元,A型体温枪的价格比B型高50元,B型体温枪的数量是A型的两倍.(1)、求每只A型、B型体温枪的价格;(2)、若购进B型体温枪的数量不超过A型体温枪的2倍,设购进A型体温枪x只,这100只体温枪的总费用为y元.
(1)、求出点 ,点 的坐标.(2)、 是直线 上一动点,且 和 的面积相等,求点 坐标.(3)、如图2,平移直线 l ,分别交 x 轴, y轴于交于点 A , B ,过点 C 作平行于 y 轴的直线m ,在直线 m 上是否存在点 Q ,使得 △ABQ 是等腰直角三角形?若存在,请直接写出所有符合条件的点 Q 的坐标.21. 12月,浙江突发疫情,我市立即启动疫情应急处置模拟演练.为配合演练顺利开展,某校需要购进A、B两款体温枪共100只.已知购进A型体温枪花费1000元,B型体温枪花费1500元,A型体温枪的价格比B型高50元,B型体温枪的数量是A型的两倍.(1)、求每只A型、B型体温枪的价格;(2)、若购进B型体温枪的数量不超过A型体温枪的2倍,设购进A型体温枪x只,这100只体温枪的总费用为y元.①求y关于x的函数关系式;
②某校实际购买时,发现某店对A型体温枪进行降价处理,比原价降低a元出售( , 且a为正整数),且限定一次性最多购买A型体温枪50只,当a满足什么条件时,能使该校购进这100只体温枪总费用最小.
22. 甲,乙两同学住在同一小区,是某学校的同班同学,小区和学校在一笔直的大街上,距离为2560米,在该大街上,小区和学校附近各有一个公共自行车取(还)车点,甲从小区步行去学校,乙比甲迟出发,步行到取车点后骑公共自行车去学校,到学校旁还车点后立即步行到学校(步行速度不变,不计取还车的时间).设甲步行的时间为x(分),图1中的线段OM和折线分别表示甲、乙同学离小区的距离y(米)与x(分)的函数关系的图象;图2表示甲、乙两人的距离s(米)与x(分)的函数关系的图象(一部分).根据图1、图2的信息,解答下列问题: (1)、分别求甲、乙两同学的步行速度与乙骑自行车的速度;(2)、求乙同学骑自行车时,y与x的函数关系式和a的值;(3)、补画完整图2,并用字母标注所画折线的终点及转折点,写出它们的坐标.23. 在平面直角坐标系中,点A的坐标为(4,0),直线l是经过点(0, )且平行于x轴的直线,点B在直线l上,连接AB,设点B的横坐标为m(m>0).
(1)、分别求甲、乙两同学的步行速度与乙骑自行车的速度;(2)、求乙同学骑自行车时,y与x的函数关系式和a的值;(3)、补画完整图2,并用字母标注所画折线的终点及转折点,写出它们的坐标.23. 在平面直角坐标系中,点A的坐标为(4,0),直线l是经过点(0, )且平行于x轴的直线,点B在直线l上,连接AB,设点B的横坐标为m(m>0). (1)、如图1,当m=9时,以AB为直角边作等腰直角三角形ABC,使∠BAC=90°,求直线BC的函数表达式.(2)、在图2中以AB为直角边作等腰直角三角形ABD,使∠ABD=90°,连结OD,求△AOD的面积(用含m的代数式表示).(3)、在图3中以AB为直角边作等腰直角三角形ABP,当点P落在直线y= x+ 上时,求m的值.24. 【探索发现】如图1,等腰直角三角形中, , , 直线经过点C,过A作于点D.过B作于点E,则 , 我们称这种全等模型为“k型全等”.(不需要证明)
(1)、如图1,当m=9时,以AB为直角边作等腰直角三角形ABC,使∠BAC=90°,求直线BC的函数表达式.(2)、在图2中以AB为直角边作等腰直角三角形ABD,使∠ABD=90°,连结OD,求△AOD的面积(用含m的代数式表示).(3)、在图3中以AB为直角边作等腰直角三角形ABP,当点P落在直线y= x+ 上时,求m的值.24. 【探索发现】如图1,等腰直角三角形中, , , 直线经过点C,过A作于点D.过B作于点E,则 , 我们称这种全等模型为“k型全等”.(不需要证明)
【迁移应用】已知:直线的图象与x轴、y轴分别交于A、B两点.
(1)、如图2,当时,在第一象限构造等腰直角 , ;
①直接写出 , ;
②点E的坐标;
(2)、如图3,当k的取值变化,点A随之在轴负半轴上运动时,在y轴左侧过点B作 , 并且 , 连接 , 问的面积是否发生变化?(填“变”或“不变”),若不变,其值为;若变,请说明理由; (3)、【拓展应用】如图4,当时,直线与y轴交于点D,点、Q分别是直线l和直线上的动点,点C在x轴上的坐标为 , 当是以为斜边的等腰直角三角形时,点Q的坐标是 .
(3)、【拓展应用】如图4,当时,直线与y轴交于点D,点、Q分别是直线l和直线上的动点,点C在x轴上的坐标为 , 当是以为斜边的等腰直角三角形时,点Q的坐标是 .