2023年浙教版数学八年级上册5.5一次函数的简单应用 同步测试(培优版)
试卷更新日期:2023-10-03 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 不论取何值,点均不在直线上,那么的值为( )A、 B、 C、 D、2. 已知一次函数的图象与的图象交于点.则对于不等式 , 下列说法正确的是( )A、当时, B、当时, C、当且时, D、当且时,3. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , , 则内部的格点个数是( )A、266 B、270 C、271 D、2854. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
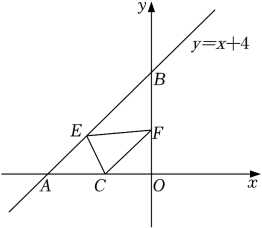 A、 , B、 , C、 , D、 ,5. 在密码学中、直接可以看到的内容称为明码,对明码进行某种处理后得到的内容称为密码.有一种密码,将英文26个字母a,b,c,…,z(不分大小写)依次对应1,2,3,…,26这26个自然数(见表格).当明码对应的序号x为奇数时,密码对应的序号;当明码对应的序号x为偶数时,密码对应的序号 . 按上述规定,明码和密码相同的序号为( )
A、 , B、 , C、 , D、 ,5. 在密码学中、直接可以看到的内容称为明码,对明码进行某种处理后得到的内容称为密码.有一种密码,将英文26个字母a,b,c,…,z(不分大小写)依次对应1,2,3,…,26这26个自然数(见表格).当明码对应的序号x为奇数时,密码对应的序号;当明码对应的序号x为偶数时,密码对应的序号 . 按上述规定,明码和密码相同的序号为( )字母
a
b
c
d
e
f
g
h
i
j
k
l
m
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
字母
n
o
p
q
r
s
t
u
v
w
x
y
z
序号
14
15
16
17
18
19
20
21
22
23
24
25
26
A、3 B、26 C、3和26 D、1和266. 已知直线 过点 且与x轴相交夹角为30度,P为直线 上一动点, 为x轴上两点,当 时取到最小值时,P的坐标为( )A、 B、 C、 D、7. 已知直线 : 与直线 : 都经过 ,直线 交y轴于点 ,交x轴于点A,直线 交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组 的解为 ;② 为直角三角形;③ ;④当 的值最小时,点P的坐标为 其中正确的说法个数有 A、1个 B、2个 C、3个 D、4个8. 为培养同学们的创新精神,某校举办校园科技节活动,八年级同学进行了机器人行走性能试验.在试验场地有A,B,C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A,B两点同时同向出发,历时8分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与它们的行走时间x(分钟)之间的函数图象,若前3.5分钟甲机器人的速度不变,则出发( )分钟后两机器人最后一次相距6米.
A、1个 B、2个 C、3个 D、4个8. 为培养同学们的创新精神,某校举办校园科技节活动,八年级同学进行了机器人行走性能试验.在试验场地有A,B,C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A,B两点同时同向出发,历时8分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与它们的行走时间x(分钟)之间的函数图象,若前3.5分钟甲机器人的速度不变,则出发( )分钟后两机器人最后一次相距6米. A、6 B、6.4 C、6.8 D、7.29. 甲,乙两车分别从A, B两地同时出发,相向而行.乙车出发2h后休息,当两车相遇时,两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h), 甲,乙两车到B地的距离分别为y1(km), y2(km), y1 , y2关于x的函数图象如图.下列结论:①甲车的速度是 km/h;②乙车休息了0.5h;③两车相距a km时,甲车行驶了 h.正确的是( )
A、6 B、6.4 C、6.8 D、7.29. 甲,乙两车分别从A, B两地同时出发,相向而行.乙车出发2h后休息,当两车相遇时,两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h), 甲,乙两车到B地的距离分别为y1(km), y2(km), y1 , y2关于x的函数图象如图.下列结论:①甲车的速度是 km/h;②乙车休息了0.5h;③两车相距a km时,甲车行驶了 h.正确的是( ) A、①② B、①③ C、②③ D、①②③10. 如图,平面直角坐标系 中,点 的坐标为 , 轴,垂足为 ,点 从原点 出发向 轴正方向运动,同时,点 从点 出发向点 运动,当点 到达点 时,点 、 同时停止运动,若点 与点 的速度之比为 ,则下列说法正确的是( )
A、①② B、①③ C、②③ D、①②③10. 如图,平面直角坐标系 中,点 的坐标为 , 轴,垂足为 ,点 从原点 出发向 轴正方向运动,同时,点 从点 出发向点 运动,当点 到达点 时,点 、 同时停止运动,若点 与点 的速度之比为 ,则下列说法正确的是( )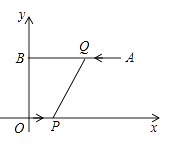 A、线段 始终经过点 B、线段 始终经过点 C、线段 始终经过点 D、线段 不可能始终经过某一定点
A、线段 始终经过点 B、线段 始终经过点 C、线段 始终经过点 D、线段 不可能始终经过某一定点二、填空题(每空3分,共18分)
-
11. 如图, 将一块等腰直角三角板 ABC放置在平面直角坐标系中, ∠ACB = 90°,AC = BC,点 A在 y轴的正半轴上,点C在 x轴的负半轴上,点 B在第二象限, AC所在直线的函数表达式是 y = x + 2,若保持 AC的长不变,当点 A在 y轴的正半轴滑动,点 C随之在 x轴的负半轴上滑动, 则在滑动过程中, 点 B与原点 O的最大距离 是.
 12. 当m,n是正实数,且满足m+n=mn时,就称点P(m, )为“完美点”.已知点A(1,6)与点B的坐标满足y=﹣x+b,且点B是“完美点”.则点B的坐标是 .13. 某日,王艳骑自行车到位于家正东方向的演奏厅听音乐会.王艳离家5分钟后自行车出现故障而且发现没有带钱包,王艳立即打电话通知在家看报纸的爸爸骑自行车赶来送钱包(王艳打电话和爸爸准备出门的时间忽略不计),同时王艳以原来一半的速度推着自行车继续走向演奏厅.爸爸接到电话后,立刻出发追赶王艳,追上王艳的同时,王艳坐上出租车并以爸爸速度的2倍赶往演奏厅(王艳打车和爸爸将钱包给王艳的时间忽略不计),同时爸爸立刻掉头以原速赶到位于家正西方3900米的公司上班,最后王艳比爸爸早到达目的地.在整个过程中,王艳和爸爸保持匀速行驶.如图是王艳与爸爸之间的距离y(米)与王艳出发时间x(分钟)之间的函数图象,则王艳到达演奏厅时,爸爸距离公司米.
12. 当m,n是正实数,且满足m+n=mn时,就称点P(m, )为“完美点”.已知点A(1,6)与点B的坐标满足y=﹣x+b,且点B是“完美点”.则点B的坐标是 .13. 某日,王艳骑自行车到位于家正东方向的演奏厅听音乐会.王艳离家5分钟后自行车出现故障而且发现没有带钱包,王艳立即打电话通知在家看报纸的爸爸骑自行车赶来送钱包(王艳打电话和爸爸准备出门的时间忽略不计),同时王艳以原来一半的速度推着自行车继续走向演奏厅.爸爸接到电话后,立刻出发追赶王艳,追上王艳的同时,王艳坐上出租车并以爸爸速度的2倍赶往演奏厅(王艳打车和爸爸将钱包给王艳的时间忽略不计),同时爸爸立刻掉头以原速赶到位于家正西方3900米的公司上班,最后王艳比爸爸早到达目的地.在整个过程中,王艳和爸爸保持匀速行驶.如图是王艳与爸爸之间的距离y(米)与王艳出发时间x(分钟)之间的函数图象,则王艳到达演奏厅时,爸爸距离公司米. 14. 秤是我国传统的计重工具,为了方便了人们的生活.如图,我们可以用秤砣到秤纽的水平距离得出秤构上所挂物体的重量,称重时,若称杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.在上表x,y的数据中,发现有一对数据记录不符合题意.当y为7斤时,对应的水平距离为 .
14. 秤是我国传统的计重工具,为了方便了人们的生活.如图,我们可以用秤砣到秤纽的水平距离得出秤构上所挂物体的重量,称重时,若称杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.在上表x,y的数据中,发现有一对数据记录不符合题意.当y为7斤时,对应的水平距离为 .
x(厘米)
1
2
4
7
11
12
y(斤)
0.75
1.00
2.00
2.25
3.25
3.50
15. 某快递公司每天上午7:00-8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法: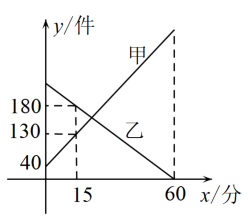
①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件数量为4件;
③8:00时,甲仓库内快件数为600件;
④7:20时,两仓库快递件数相同.
其中正确的个数为 .
16. “双11”当天,重庆顺风快递公司出动所有车辆分上午、下午两批往成都送件,该公司共有甲、乙、丙三种车型,其中甲型车数量占公司车辆总数的 ,乙型车辆是丙型车数量的2倍,上午安排甲车数量的 ,乙车数量的 ,丙车数量的 进行运输,且上午甲、乙、丙三种车型每辆载货量分别为15吨,10吨,20吨,则上午刚好运完当天全部快件重量的 ;下午安排剩下的所有车辆运输完当天剩下的所有快件,且下午甲、乙、丙三种车型每辆载货量分别不得超过20吨,12吨,16吨,下午乙型车实际载货量为下午甲型车每辆实际载货量的 .已知同种货车每辆的实际载货量相等,甲、乙、丙三种车型每辆车下午的运输成本分别为50元/吨,90元/吨,60元/吨.则下午运输时,一辆甲种车、一辆乙种车、一辆丙种车总的运输成本最少为元.三、解答题(共9题,共72分)
-
17. 为提升学生的文学素养,培养学生的阅读兴趣,某校准备购进A,B两种图书.经调查,购进A种图书费用y元与购进A种图书本数x之间的函数关系如图所示,B种图书每本20元.
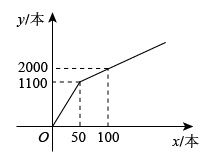 (1)、当和时,求y与x之间的函数关系式;(2)、现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.
(1)、当和时,求y与x之间的函数关系式;(2)、现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.①当时,求出w与x间的函数表达式;
②若购进A种图书不少于60本,且不超过B种图书本数的2倍,那么应该怎样分配购买A,B两种图书才能使总费用最少?最少总费用多少元?
18. 现从某养殖基地运送144箱鱼苗到、两村养殖,若大、小货车共用14辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往、两村的运费如下表:养殖基地车型
村(元/辆)
村(元/辆)
大货车
800
900
小货车
400
600
(1)、求大、小货车各多少辆?(2)、现安排其中10辆货车前往村,其余货车前往村,设前往村的大货车为辆,前往、两村总费用为元,求出与的函数解析式,并直接写出自变量的取值范围;(3)、在(2)的条件下,若运往村的鱼苗不少于箱,请写出总费用最少时的货车调配方案,并求出最少费用.19. 图中折线表示一骑车人小明离学校的距离与离开学校时间的关系.小明匀速骑行到达图书馆,在图书馆阅读一段时间,然后返回学校;回学校途中,匀速骑行后减速,继续匀速骑行回到学校.请你根据相关信息,解答下列问题: (1)、图书馆与学校距离是 , 小明在图书馆阅读时长为h,小明前往图书馆的平均速度是 , 当时,y关于x的解析式为;(2)、小明刚开始离开学校的时候,另一骑车人小华同时出发,从图书馆沿着相同路线以速度匀速前往学校,到达学校后马上骑车以速度匀速前往图书馆.
(1)、图书馆与学校距离是 , 小明在图书馆阅读时长为h,小明前往图书馆的平均速度是 , 当时,y关于x的解析式为;(2)、小明刚开始离开学校的时候,另一骑车人小华同时出发,从图书馆沿着相同路线以速度匀速前往学校,到达学校后马上骑车以速度匀速前往图书馆.①请问小华速度为何范围时,小华与小明可以在时相遇;
②当时,请求出x为何值时小华与小明相距 .
20. 如图,在正方形中, , 动点F,E分别从点A,B出发,F点沿着运动,到达C点停止运动,点E沿着运动,到达D点停止运动,连接EC,BF,已知F点的速度且 , 令 , 运动时间为x.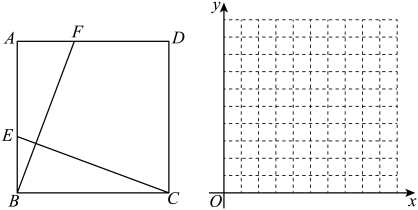
请回答下列问题:
(1)、请直接写出与x之间的函数关系式以及对应的x的取值范围;(2)、请在直角坐标系中画出的图像,并写出函数的一条性质;(3)、根据图形直接估计当时x的取值范围.(结果保留1位小数,误差不超过0.2)21. 如图,在平面直角坐标系中,已知直线:经过 , 动点在直线:上,直线和交于点 , 设点的横坐标为 , (1)、求的值和点的坐标.(2)、过点作轴的平行线交直线于点 , 当以、、、为顶点的四边形为平行四边形时,求的值;(3)、过点作轴的垂线交轴于点 , 以为边向右作正方形 , 当正方形的顶点或落在直线上时,直接写出的值.22. 甲、乙两地相距3000千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段表示货车离甲地距离千米与时间小时之间的函数关系;线段表示轿车离甲地距离千米与时间小时之间的函数关系.点在线段上,请根据图象解答下列问题:
(1)、求的值和点的坐标.(2)、过点作轴的平行线交直线于点 , 当以、、、为顶点的四边形为平行四边形时,求的值;(3)、过点作轴的垂线交轴于点 , 以为边向右作正方形 , 当正方形的顶点或落在直线上时,直接写出的值.22. 甲、乙两地相距3000千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段表示货车离甲地距离千米与时间小时之间的函数关系;线段表示轿车离甲地距离千米与时间小时之间的函数关系.点在线段上,请根据图象解答下列问题: (1)、试求点的坐标;(2)、当轿车与货车相遇时,求此时的值;(3)、在整个过程中 , 问在什么范围时,轿车与货车之间的距离小于30千米.23. 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)、试求点的坐标;(2)、当轿车与货车相遇时,求此时的值;(3)、在整个过程中 , 问在什么范围时,轿车与货车之间的距离小于30千米.23. 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题: (1)、求张强返回时的速度;(2)、妈妈比按原速返回提前多少分钟到家?(3)、请直接写出张强与妈妈何时相距1000米?24. 探究通过维修路段的最短时长.
(1)、求张强返回时的速度;(2)、妈妈比按原速返回提前多少分钟到家?(3)、请直接写出张强与妈妈何时相距1000米?24. 探究通过维修路段的最短时长.素材1:如图1,某路段(A-B-C-D 段)需要维修,临时变成双向交替通行,故在A,D处各设置红绿灯指导交通(仅设置红灯与绿灯).
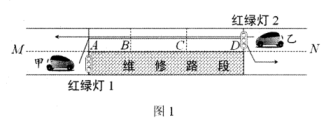
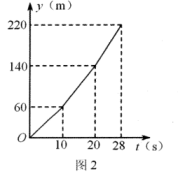
素材2:甲车先由A→D通行,乙车再由D→A通行,甲车经过AB,BC,CD段的时间分别为10s,10s,8s,它的路程y (m)与时间t(s)的关系如图2所示;两车经过BC段的速度相等,乙车经过AB段的速度是10m/s.
素材3:红绿灯1,2每114秒一个循环,每个循环内红灯、绿灯的时长如图3,且每次双向红灯时,已经进入AD段的车辆都能及时通过该路段.

[任务1]求A-B-C-D段的总路程和甲车经过BC段的速度.
[任务2]在图4中补全乙车通过维修路段时行驶的路程y(m)与时间t(s)之间的函数图象.
[任务3]丙车沿NM方向行驶,经DA段的车速与乙车经过时的速度相同,在DN段等红灯的车辆开始行驶后速度为8m/s,等红灯时车流长度每秒增加2m,问丙车在DN段从开始等待至离开点A至少需要几秒钟?
 25. 阅读下列材料,并完成任务.
25. 阅读下列材料,并完成任务.以方程的解为坐标的点的全体叫做方程的图象.我们知道,二元一次方程有无数组解,我们把每一组解用有序数对表示,就可以描出无数个以方程的解为坐标的点,这无数个点组成一条直线,反过来,这条直线上任意一点的坐标是方程的解.
 (1)、任务一:填空
(1)、任务一:填空①如图1,在平面直角坐标系中,点是方程的图象上一点,点的坐标为 , 则方程方程的解.(填“是”或“不是”)
②在平面直角坐标系中,点的坐标为 , 则点方程的图象上.(填“在”或“不在”)
点的坐标为 , 则点方程的图象上.(填“在”或“不在”)
(2)、任务二:如图2,在平面直角坐标系中,方程的图象与方程的图象交于点 , 则二元一次方程组的解为 .(3)、任务三:上述用图形的方法得出二元一次方程组的解的过程,主要体现的数学思想是____.(填出下列选项的字母代号即可)A、转化思想 B、数形结合思想 C、方程思想