2023年浙教版数学八年级上册5.5一次函数的简单应用 同步测试(基础版)
试卷更新日期:2023-10-03 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,反映的是西安某景点五一当天某段时间游客人数(人)随时间(时)的变化情况,则这一天人数最多的时刻大约是( )
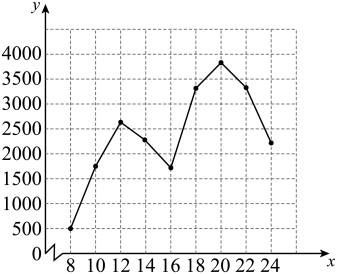 A、10时 B、12时 C、18时 D、20时2. 某项目化学习小组的同学在水中掺入酒精,充分混合后,放入冰箱冷冻室.根据实验数据作出混合液温度()随时间()变化而变化的图象.下列说法不正确的是( )
A、10时 B、12时 C、18时 D、20时2. 某项目化学习小组的同学在水中掺入酒精,充分混合后,放入冰箱冷冻室.根据实验数据作出混合液温度()随时间()变化而变化的图象.下列说法不正确的是( ) A、在这个变化过程中,自变量是时间,因变量是混合液的温度. B、混合液的温度随着时间的增大而下降. C、当时间为时,混合液的温度为 D、当时,混合液的温度保持不变3. 地表以下岩层的湿度随着所处深度的变化而变化,在某个地点与的部分对应数据如下表,则该地y与x的函数关系可以近似的表示为
A、在这个变化过程中,自变量是时间,因变量是混合液的温度. B、混合液的温度随着时间的增大而下降. C、当时间为时,混合液的温度为 D、当时,混合液的温度保持不变3. 地表以下岩层的湿度随着所处深度的变化而变化,在某个地点与的部分对应数据如下表,则该地y与x的函数关系可以近似的表示为所处深度
2
3
5
7
10
13
地表以下岩层的温度
90
125
195
265
370
475
则该地y与x的关系可以近似的表示为( )
A、 B、 C、 D、4. 在某一阶段,某商品的销售量与销售价之间存在如下关系:销售价/元
90
100
110
120
130
140
销售量/件
90
80
70
60
50
40
设该商品的销售价为x元,销售量为y件,估计当x=127时,y的值为( )
A、63 B、59 C、53 D、435. 如图,在弹性限度内,弹簧的长度y(cm)与所挂物体的质量x(kg)之间是一次函数关系,则弹簧不挂物体时的长度为( )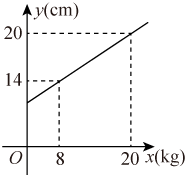 A、8cm B、10cm C、11cm D、12cm6. 某品牌鞋子的长度ycm与鞋子的码数x之间满足一次函数关系.若23码鞋子的长度为16.5cm,44码鞋子的长度为27cm,则38码鞋子的长度为( )A、23cm B、24cm C、25cm D、26cm7. 把一个长为8,宽为3的长方形的宽增加x(0≤x<5),长不变,所得长方形的面积y关于x的函数表达式为( )A、y=24﹣x B、y=8x﹣24 C、y=8x D、y=8x+248. 已知一次函数的图象如图所示, 则方程的解可能是( )
A、8cm B、10cm C、11cm D、12cm6. 某品牌鞋子的长度ycm与鞋子的码数x之间满足一次函数关系.若23码鞋子的长度为16.5cm,44码鞋子的长度为27cm,则38码鞋子的长度为( )A、23cm B、24cm C、25cm D、26cm7. 把一个长为8,宽为3的长方形的宽增加x(0≤x<5),长不变,所得长方形的面积y关于x的函数表达式为( )A、y=24﹣x B、y=8x﹣24 C、y=8x D、y=8x+248. 已知一次函数的图象如图所示, 则方程的解可能是( )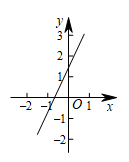 A、x=1 B、x= C、x= D、x=-19. 如图,:和:相交于 , 则解集为( )
A、x=1 B、x= C、x= D、x=-19. 如图,:和:相交于 , 则解集为( )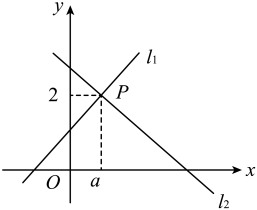 A、 B、 C、 D、10. 已知二元一次方程组的解为 , 则在同一平面直角坐标系中,直线:与直线:的交点坐标为( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知二元一次方程组的解为 , 则在同一平面直角坐标系中,直线:与直线:的交点坐标为( )A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克
1
1.5
2
2.5
3
3.5
4
烤制时间/分
60
80
100
120
140
160
180
设鸭的质量为千克,烤制时间为 , 估计当千克时,的值为分.
12. 已知函数y=ax+b和y=kx的图象交于点P(-4,-2),则二元一次方程组的解是 .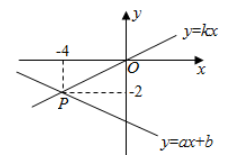 13. 如图,函数y=2x和y=ax+b的图象相交于点A(m,3),则关于x的不等式2xax+b的最小整数解为 .
13. 如图,函数y=2x和y=ax+b的图象相交于点A(m,3),则关于x的不等式2xax+b的最小整数解为 .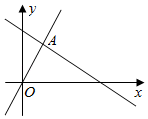 14. 如图,直线AB是一次函数的图象,若关于x的方程的解是 , 则直线AB的函数关系式为 .
14. 如图,直线AB是一次函数的图象,若关于x的方程的解是 , 则直线AB的函数关系式为 .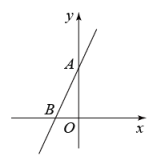 15. 小明家到学校的路程是米,小明从家出发,以平均每分钟米的速度步行去上学,则他离学校的路程(米)与行走的时间(分)之间的关系式是 .16. 科学家研究发现声音在空气中传播的速度y(米/秒)与气温有的关系,若今天的气温是 , 则声音的传播速度是米/秒.
15. 小明家到学校的路程是米,小明从家出发,以平均每分钟米的速度步行去上学,则他离学校的路程(米)与行走的时间(分)之间的关系式是 .16. 科学家研究发现声音在空气中传播的速度y(米/秒)与气温有的关系,若今天的气温是 , 则声音的传播速度是米/秒.三、解答题(共8题,共66分)
-
17. 如图, , 分别表示两个一次函数的图象,它们相交于点P.
 (1)、求出两条直线的函数关系式(2)、点P的坐标可看作是哪个二元一次方程组的解.18. 公路上依次有A,B,C三个汽车站,上午8时,小明骑自行车从A,B两站之间距离A站8km处出发,向C站匀速前进,他骑车的速度是每小时16.5km,若A,B两站间的路程是26km,B,C两站的路程是15km.(1)、在小明所走的路程与骑车用去的时间这两个变量中,哪个是自变量?哪个是因变量?(2)、设小明出发x小时后,离A站的路程为ykm,请写出y与x之间的关系式.(3)、小明在上午9时是否已经经过了B站?19. “五一”假期,小明一家将随团到某风景区旅游,集体门票的收费标准是:25人以内(含25人),每人30元;超过25人时,超过部分每人20元.(1)、写出应收门票费y(元)与游览人数x(人)之间的关系式;(2)、若小明一家所在的旅游团购门票花了1250元,则该旅游团共有多少人.20. 在给出的网格中画出一次函数 的图象,并结合图象求:
(1)、求出两条直线的函数关系式(2)、点P的坐标可看作是哪个二元一次方程组的解.18. 公路上依次有A,B,C三个汽车站,上午8时,小明骑自行车从A,B两站之间距离A站8km处出发,向C站匀速前进,他骑车的速度是每小时16.5km,若A,B两站间的路程是26km,B,C两站的路程是15km.(1)、在小明所走的路程与骑车用去的时间这两个变量中,哪个是自变量?哪个是因变量?(2)、设小明出发x小时后,离A站的路程为ykm,请写出y与x之间的关系式.(3)、小明在上午9时是否已经经过了B站?19. “五一”假期,小明一家将随团到某风景区旅游,集体门票的收费标准是:25人以内(含25人),每人30元;超过25人时,超过部分每人20元.(1)、写出应收门票费y(元)与游览人数x(人)之间的关系式;(2)、若小明一家所在的旅游团购门票花了1250元,则该旅游团共有多少人.20. 在给出的网格中画出一次函数 的图象,并结合图象求:
①方程 的解;
②不等式 的解集;
③不等式 的解集.
21. 李叔叔要用篱笆围成一个长方形的果园,已知长方形的宽为 米,长比宽长 米.当长方形的宽由小到大变化时,长方形的面积也随之发生变化.(1)、求长方形果园的面积 (平方米)与 之间的关系式;(2)、当长方形果园的宽为 米时,求长方形果园的面积;(3)、当长方形果园的长恰好是宽的 倍时,求长方形果园的面积.22. 我市为创建“国家级森林城市”,政府决定对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗.某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价及成活率如表:品种
购买价(元/棵)
成活率
甲
20
90%
乙
32
95%
设购买甲种树苗x棵,承包商获得的利润为y元.请根据以上信息解答下列问题:
(1)、设y与x之间的函数关系式,并写出自变量x的取值范围;
(2)、承包商要获得不低于中标价16%的利润,应如何选购树苗?(3)、政府与承包商的合同要求,栽植这批树苗的成活率必须不低于93%,否则承包商出资补栽;若成货率达到94%以上(含94%),则政府另给予工程款总额6%的奖励,该承包商应如何选购树苗才能获得最大利润?最大利润是多少?23. 甲、乙两地打电话需付的电话费y(元)是随时间t(分钟)的变化而变化的,试根据下表列出的几组数据回答下列问题:通话时间t(分钟)
1
2
3
4
5
6
…
电话费y(元)
0.15
0.30
0.45
0.6
0.75
0.9
…
(1)、自变量是 , 因变量是(2)、写出电话费y(元)与通话时间t(分钟)之间的关系式;(3)、若小明通话15分钟,则需付话费多少元?(4)、若小明某次通话后,需付话费6元,则小明通话多少分钟?24. 一辆汽车油箱内有油56升,从某地出发,每行驶1千米,耗油0.08升,如果设油箱内剩油量为y(升),行驶路程为x(千米),则y随x的变化而变化.(1)、在上述变化过程中,自变量是 , 因变量是 .(2)、用表格表示汽车从出发地行驶100千米、200千米、300千米、400千米时的剩油量.请将表格补充完整:行驶路程x(千米)
100
200
300
400
油箱内剩油量y(升)
40
24
(3)、试写出y与x的关系式是 .(4)、这辆汽车行驶350千米时,剩油量是多少?汽车油箱内剩油8升时,汽车行驶了多少千米?