2023年浙教版数学八年级上册5.4一次函数的图象 同步测试(培优版)
试卷更新日期:2023-10-03 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 直线y=x+n与直线y=mx+3n(m是常数,m≠0且m≠1)交于点A , 当n的值发生变化时,点A到直线y=x-3的距离总是一个定值,则m的值是( )A、3 B、2 C、 D、2. 如果函数y=kx-6和y=-2x+a的图象的交点在第三象限,那么k,a的取值范围是( )A、k>0,a>-6 B、k>0,a<-6 C、k>0,a>6 D、k<0,a>63. 一次函数y= kx+b的图象过点P (2,8),且分别与x轴和y轴的正半轴交于A,B两点,点O为坐标原点.当△AOB面积最小时,则k+b的值为( )A、10 B、12 C、14 D、164. 数形结合是解决数学问题常用的思想方法.如图,直线 和直线 相交于点 ,根据图象可知,不等式 的解集是( )
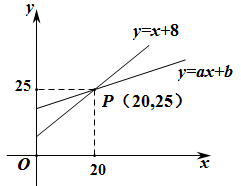 A、 B、 C、 D、5. 记实数x1 , x2 , …,xn中的最大数为max{x1 , x2 , …,xn},例如max{﹣2,0,2}=2,则函数y=max{﹣3x﹣3,2﹣x,x}的图象大致为( )A、
A、 B、 C、 D、5. 记实数x1 , x2 , …,xn中的最大数为max{x1 , x2 , …,xn},例如max{﹣2,0,2}=2,则函数y=max{﹣3x﹣3,2﹣x,x}的图象大致为( )A、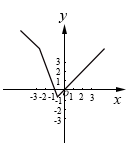 B、
B、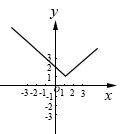 C、
C、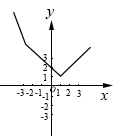 D、
D、 6. 如图,直线y=﹣x+4分别与x轴、y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是( )
6. 如图,直线y=﹣x+4分别与x轴、y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是( )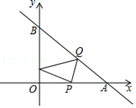 A、(2,2) B、(2.5,1.5) C、(3,1) D、(1.5,2.5)7. 关于x的一次函数 , 当时,y的最大值是( )A、 B、 C、 D、8. 一次函数的图象与x轴、y轴分别交于点A、B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点共有( )A、90个 B、92个 C、104个 D、106个9. 一次函数( , k、b是常数)与( , m是常数)的图像交于点 , 下列结论正确的序号是( )
A、(2,2) B、(2.5,1.5) C、(3,1) D、(1.5,2.5)7. 关于x的一次函数 , 当时,y的最大值是( )A、 B、 C、 D、8. 一次函数的图象与x轴、y轴分别交于点A、B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点共有( )A、90个 B、92个 C、104个 D、106个9. 一次函数( , k、b是常数)与( , m是常数)的图像交于点 , 下列结论正确的序号是( )①关于的方程的解为;
②一次函数()图像上任意不同两点和满足:;
③若(),则;
④若 , 且 , 则当时, .
A、②③④ B、①②④ C、①②③ D、①②③④10. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …,An在x轴上,点B1 , B2 , …,B在直线上,若点A1的坐标为(1,0),且 , , …,都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1 , S2 , …,Sn , 则Sn可表示为( )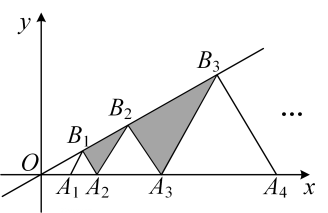 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
11. 已知直线y=﹣x+2与直线y=2x+4相交于点A,与x轴分别交于B,C两点,若点D(m,﹣2m+1)落在△ABC内部(不含边界),则m的取值范围是 .12. 在平面直角坐标系中,已知一次函数的图象与轴交于 , 与轴交于点.点是直线上的一个动点,将点向下平移4个单位长度得到点 , 若线段与轴有一个公共点,设点的横坐标为 , 则的取值范围是 .13. 已知点A的坐标是 , 点B是正比例函数 的图象上一点,若只存在唯一的点B,使 为等腰三角形,则k的取值范围是.14. 已知直线与(其中k为正整数),记与x轴围成的三角形面积为 , 则 .15. 将函数(为常数)的图象位于轴下方的部分沿轴翻折至其上方后,所得的折线是函数(为常数)的图象.在以下四个结论中正确的是(填序号).
①当时,函数的图象与轴的交点是;
②当时,函数以的图象与轴的交点是;
③不论为任意常数,函数的最小值都是0;
④若图象在直线下方的点的横坐标满足 , 则的取值范围为 .
16. 定义:在平面直角坐标系中,若点M关于直线的对称点在的内部(不包含边界),则称点M是关于直线的“伴随点”.如图,已知三点,连接 , 以为边作 . 若在直线上存在点N,使得点N是关于直线的“伴随点”,则n的取值范围是 .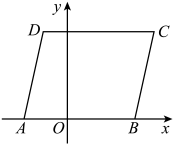
三、解答题(共8题,共72分)
-
17. 设函数y1=ax+b,y2=bx+a(a,b为常数,ab≠0且a≠b),函数y1和y2的图象的交点为点P.(1)、求点P的横坐标.(2)、已知点P在第一象限,函数y2的值随x的增大而增大.
①当x=2时,y2﹣y1=2,求a的取值范围.
②若点P的坐标是(1,1),且a>b,求证:当x=2时,y1﹣y2<
18. 定义:叫做关于直线x=m的“分边折叠函数”.(1)、已知“分边折叠函数”①直接写出该函数与y轴的交点坐标;
②若直线y=4x+t与该函数只有一个交点,求t的取值范围;
(2)、已知“分边折叠函数”的图象被直线x=m与y轴所夹的线段长为 , 则k的值为 .19. 定义:函数 叫做关于m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B.(1)、关于1的对称函数 与直线 交于点C,如图.① , , .
②P为关于1的对称函数图象上一点(点P不与点C重合),当 时,求点P的坐标;
(2)、当直线 与关于m的对称函数有两个交点时,求m的取值范围. 20. 函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索,画函数 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如下图所示:
20. 函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索,画函数 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如下图所示:x
……
-3
-2
-1
0
1
2
3
……
y
……
6
4
2
0
2
4
6
……
经历同样的过程画函数 和 的图象如下图所示,观察发现:三个函数的图象都是由两条射线组成的轴对称图形:三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.
(1)、请直接写出 与 的交点坐标和函数 的对称轴;(2)、在所给的平面直角坐标系内画出函数 的图象(不列表),并写出函数 的一条性质;(3)、结合函数图象,直接写出不等式 时x的取值范围. 21. 在平面直角坐标系中,给出以下定义:对于x轴上点M(a,0)(其中a为正整数)与坐标平面内一点N,若y轴上存在点T,使得 , 且 , 则称点N为a宝点,如示例图,我们可知点N(-1,0)为1宝点,理由如下:在x轴上取点M(1,0),以MN为斜边作等腰直角三角形MNT,可以算得一个点T(0,1),它是在y轴上的,因此点N(-1,0)为1宝点.
21. 在平面直角坐标系中,给出以下定义:对于x轴上点M(a,0)(其中a为正整数)与坐标平面内一点N,若y轴上存在点T,使得 , 且 , 则称点N为a宝点,如示例图,我们可知点N(-1,0)为1宝点,理由如下:在x轴上取点M(1,0),以MN为斜边作等腰直角三角形MNT,可以算得一个点T(0,1),它是在y轴上的,因此点N(-1,0)为1宝点. (1)、如图①,在点A(2,0),B(2,-2),C(0,1),D(-2,0)中,2宝点是点 . (填“A”“B”“C”或“D”)(2)、如图①,点M(4,0),T(0,3),若N为4宝点,求点N的坐标.(3)、如图②,若一次函数的图象上存在2宝点,求这个2宝点的坐标(4)、若一次函数图象上存在无数个3宝点,请直接写出该一次函数的解析式.22. 如图所示,在平面直角坐标系xOy中,直线l1: 交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l2 , 将直线l2绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).
(1)、如图①,在点A(2,0),B(2,-2),C(0,1),D(-2,0)中,2宝点是点 . (填“A”“B”“C”或“D”)(2)、如图①,点M(4,0),T(0,3),若N为4宝点,求点N的坐标.(3)、如图②,若一次函数的图象上存在2宝点,求这个2宝点的坐标(4)、若一次函数图象上存在无数个3宝点,请直接写出该一次函数的解析式.22. 如图所示,在平面直角坐标系xOy中,直线l1: 交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l2 , 将直线l2绕点C按逆时针方向旋转,旋转角为α(0°<α<180°). (1)、若直线l2经过点A,①求线段AC的长;②直接写出旋转角α的度数;(2)、若直线l2在旋转过程中与y轴交于D点,当△ABD、△ACD、△BCD均为等腰三角形时,求出符合条件的旋转角α的度数.(3)、若直线l2在旋转过程中与直线l1 交于点E,连OE,以OE为边作等边△OEF(点O、E、F按逆时针方向排列),连BF.请你探究线段BE,OB与BF之间的数量关系?并说明理由。23. 如图,已知直线y=﹣x+4与y轴交于点A,与x轴交于点B,过点C(1,0)作CD⊥x轴交直线AB于点D.点P是x轴上的一个动点,点E是BD的中点,在△PEF中(三顶点顺时针排列),∠PEF=90°,PE=EF.
(1)、若直线l2经过点A,①求线段AC的长;②直接写出旋转角α的度数;(2)、若直线l2在旋转过程中与y轴交于D点,当△ABD、△ACD、△BCD均为等腰三角形时,求出符合条件的旋转角α的度数.(3)、若直线l2在旋转过程中与直线l1 交于点E,连OE,以OE为边作等边△OEF(点O、E、F按逆时针方向排列),连BF.请你探究线段BE,OB与BF之间的数量关系?并说明理由。23. 如图,已知直线y=﹣x+4与y轴交于点A,与x轴交于点B,过点C(1,0)作CD⊥x轴交直线AB于点D.点P是x轴上的一个动点,点E是BD的中点,在△PEF中(三顶点顺时针排列),∠PEF=90°,PE=EF. (1)、则A、B、D三点的坐标分别为:A , B , D.(2)、如图,当点P在线段CB上时,若CP=2BP,求点F的坐标.(3)、当点P在射线CB上运动,连接AF.若S△AEF=5S△PBE , 求点P的坐标.24.
(1)、则A、B、D三点的坐标分别为:A , B , D.(2)、如图,当点P在线段CB上时,若CP=2BP,求点F的坐标.(3)、当点P在射线CB上运动,连接AF.若S△AEF=5S△PBE , 求点P的坐标.24.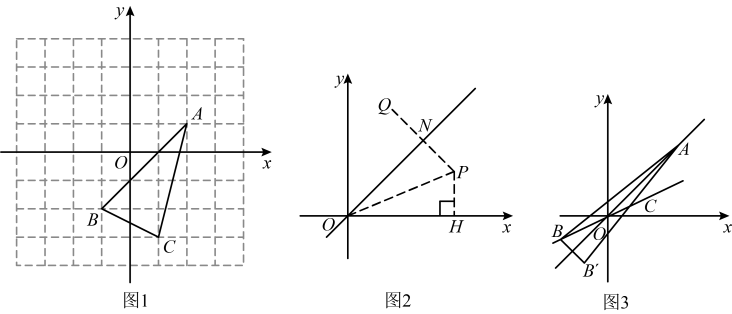 (1)、【操作思考】
(1)、【操作思考】如图1所示的网格中,建立平面直角坐标系.先画出正比例函数的图象,再画出关于正比例函数的图象对称的 .
(2)、【猜想验证】猜想:点关于正比例函数的图象对称的点Q的坐标为;
验证点在第一象限时的情况(请将下面的证明过程补充完整).
证明:如图2,点、Q关于正比例函数的图象对称,轴,垂足为H .
(3)、【应用拓展】如图3,点A坐标为 , 点B坐标为 , 点B与点关于直线对称,连接与直线交于点C , 则点C的坐标为 .