2023-2024学年浙教版数学七年级上册第1~2章核心素养提升测试卷(基础过关+能力提升)
试卷更新日期:2023-10-03 类型:单元试卷
一、选择题
-
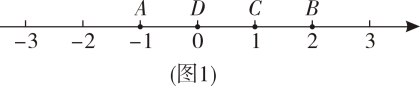
1. 的相反数是( )A、 B、 C、 D、2. 若零下摄氏度记为 , 则零上摄氏度记为( )A、 B、 C、 D、3. 计算的结果是( )A、1 B、 C、5 D、4. 下面四个数中最小的数是( )A、 B、 C、 D、5. 光在真空中的速度约为每秒万千米,用科学记数法表示千米秒.( )A、 B、 C、 D、6. 下列各式中结果为负数的是( )A、 B、 C、 D、7. 把有理数、在数轴上表示,如图所示,则下列说法正确的是( )
 A、 B、 C、 D、8. 下列算式中,结果是正数的是.( )A、 B、 C、 D、9. 计算: , , , , 归纳各计算结果中的个位数字规律,猜测的个位数字是( )A、 B、 C、 D、10. 已知整数a1 , a2 , a3 , a4 , …满足下列条件:a1=0,a2=-|a1+1|.a3=-|a2+2|,a4=-|a3+3|,…依此类推,则a2022的值为( )A、2022 B、-2022 C、-1011 D、1011
A、 B、 C、 D、8. 下列算式中,结果是正数的是.( )A、 B、 C、 D、9. 计算: , , , , 归纳各计算结果中的个位数字规律,猜测的个位数字是( )A、 B、 C、 D、10. 已知整数a1 , a2 , a3 , a4 , …满足下列条件:a1=0,a2=-|a1+1|.a3=-|a2+2|,a4=-|a3+3|,…依此类推,则a2022的值为( )A、2022 B、-2022 C、-1011 D、1011二、填空题
-
11. 用四舍五入法,将精确到百分位的近似数是 .12. 已知(x-3)x+4=1,则整数x的值是 .13. 若与互为相反数,则a的值为 .14. 计算 .15. 如果下降记作 , 那么上升记作m;如果表示增加 , 那么表示16. 数轴上点表示的数是 , 将点在数轴上平移个单位长度得到点 , 则平移后点表示的数是 .
三、解答题
-
17. 计算:(1)、;(2)、;(3)、;(4)、18. 画出数轴并把下列各数在数轴上表示出来。并用“<”把它们连接起来。
-3,-1, , 0,4,
19. 如图,点A,B分别表示数a,b(要求:尺规作图,不写作法,保留作图痕迹). (1)、在数轴上作出表示数的点C;(2)、在数轴上作出表示数的点D.20. 某市今年受台风“梅花”的影响,在抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从地出发,晚上到达地,约定向东为正方向,当天的航行路程记录如下单位:千米:
(1)、在数轴上作出表示数的点C;(2)、在数轴上作出表示数的点D.20. 某市今年受台风“梅花”的影响,在抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从地出发,晚上到达地,约定向东为正方向,当天的航行路程记录如下单位:千米:, , , , , , , .
(1)、请你帮忙确定地位于地的什么方向,距离地多少千米的地方?(2)、若冲锋舟每千米耗油升,油箱容量为升,求冲锋舟当天救灾过程中至少还需补充多少升油?21. “低碳生活”从现在做起,从我做起,据测算,公顷落叶阔叶林每年可吸收二氧化碳吨,如果每台空调制冷温度在国家提倡的摄氏度基础上调到摄氏度,相应每年减排二氧化碳千克某市仅此项就大约减排相当于公顷落叶阔叶林全年吸收的二氧化碳,若每个家庭按台空调计算,该市约有多少万户家庭?22. 某巡警骑摩托车在一条东西大道上巡逻.某天他从岗亭出发,晚上停留在A处.规定向东方向为正,当天行驶记录如下(单位:千米):+10,-8,+6,-13,+7,-12,+3,-1
(1)、A在岗亭何方?通过计算说明A距离岗亭多远?(2)、在岗亭东面6千米处有个加油站,该巡警巡逻时经过加油站次.(3)、若摩托车每行1千米耗油0.05升,那么该摩托车这天巡逻共耗油多少升?23. 阅读理解:若、、为数轴上三点,若点到的距离是点到的距离倍,我们就称点是【 , 】的好点.
例如,如图 , 点表示的数为 , 点表示的数为表示的点到点的距离是 , 到点的距离是 , 那么点是【 , 】的好点;又如,表示的点到点的距离是 , 到点的距离是 , 那么点就不是【 , 】的好点,但点是【 , 】的好点.
知识运用:如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为 .
 (1)、数所表示的点是【 , 】的好点;(2)、如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为现有一只电子蚂蚁从点出发,以个单位每秒的速度向左运动,到达点停止当为何值时,、和中恰有一个点为其余两点的好点?
(1)、数所表示的点是【 , 】的好点;(2)、如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为现有一只电子蚂蚁从点出发,以个单位每秒的速度向左运动,到达点停止当为何值时,、和中恰有一个点为其余两点的好点?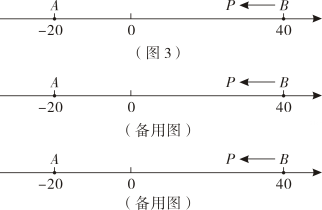 24. 阅读材料:求1+2+22+23+24+…+22017的值.
24. 阅读材料:求1+2+22+23+24+…+22017的值.解:设S=1+2+22+23+24+…+22017 , 将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22018
将下式减去上式得2S-S=22018-1,即S=22018-1
即1+2+22+23+24+…+22017=22018-1
请你仿照此法计算:
(1)、1+2+22+23+24+…+210(2)、1+3+32+33+34+…+32016 .