2023年浙教版数学八年级上册5.2函数同步测试（提高版）

试卷更新日期：2023-10-03 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 一个容器中装有一定质量的糖，向容器中加入水，随着水量的增加，糖水的浓度将降低，这个问题中自变量和因变量分别是（）

A、糖，糖水的浓度 B、水，糖水 C、糖，糖水 D、水，糖水的浓度

查看试题解析
2. 下列图象中，表示y是x的函数的个数有（）

A、1 B、2个 C、3个 D、4个

查看试题解析
3. 变量 $x$ ， $y$ 有如下关系：① $x + y = 10$ ；② $y = \frac{- 5}{x}$ ；③ $y = x - 3$ ；④ $y^{2} = 8 x$ .其中 $y$ 是 $x$ 的函数的是（）

A、①②③④ B、①②③ C、①② D、①

查看试题解析
4. 正方形的周长y是边长x的函数，则下列表示正方形周长y与边长x之间的函数关系正确的是（）

A、 $y = 2 x (x > 0)$ B、 $y = 4 x (x > 0)$ C、 $y = x_{}^{2} (x > 0)$ D、 $y = 4 x^{2} (x > 0)$

查看试题解析
5. 函数 $y = 10 x - 10$ 中，自变量x的取值范围是（）

A、 $x \geq 1$ B、 $x > 1$ C、 $x \neq 1$ D、 $x$ 为任意实数

查看试题解析
6. 下列函数中，自变量x的取值范围为 $x < 1$ 的是（）

A、 $y = \frac{1}{1 - x}$ B、 $y = 1 - \frac{1}{x}$ C、 $y = \sqrt{1 - x}$ D、 $y = \frac{1}{\sqrt{1 - x}}$

查看试题解析
7. 如图所示的计算程序中，y与x之间的函数关系式是（）

A、y＝﹣3x+2 B、y＝3x+2 C、y＝﹣3x﹣2 D、y＝3x﹣2

查看试题解析
8. 地表以下岩层的温度 $y (℃)$ 随着所处深度 $x (k m)$ 的变化而变化，在某个地点 $y$ 与 $x$ 之间的关系可以近似地用关系式 $y = 35 x + 20$ 来表示．当深度 $x$ 增加 $5 k m$ 时， $y$ 的值（）

A、减少 $175 ℃$ B、增加 $175 ℃$ C、不变 D、增加 $195 ℃$

查看试题解析
9. 弹簧挂上物体后伸长，已知一弹簧的长度 $(c m)$ 与所挂物体的质量 $(k g)$ 之间的关系如表：下列说法错误的是（）
物体的质量 $(k g)$
$0$
$1$
$2$
$3$
$4$
$5$
弹簧的长度 $(c m)$
$10$
$12.5$
$15$
$17.5$
$20$
$22.5$

A、在没挂物体时，弹簧的长度为 $10 c m$ B、弹簧的长度随物体的质量的变化而变化，物体的质量是因变量，弹簧的长度是自变量 C、在弹簧能承受的范围内，所挂物体的质量每增加 $1 k g$ ，弹簧的长度就增加 $2.5 c m$ D、在弹簧能承受的范围内，当物体的质量为 $4 k g$ 时，弹簧的长度为 $20 c m$

查看试题解析
10. 周末，乐乐去公园游玩，坐上了他向往已久的摩天轮（如图所示）．摩天轮上，乐乐离地面的高度h（米）和他坐上摩天轮后旋转的时间t（分）之间的部分关系图象如图所示，下列说法错误的是（）

A、摩天轮转动6分钟后，离地面的高度为3米 B、摩天轮转动的第3分钟和第9分钟，离地面的高度相同 C、摩天轮转动一周需要6分钟 D、乐乐离地面的最大高度是42米

查看试题解析

二、填空题（第11题3分，12-16每题4分）

11. 威海市和烟台市相距120千米，一辆汽车以v千米/时的速度从威海市开往烟台市用了t小时，若v=60，则t=；若 v=80，则t=；t是v的函数吗？答：(填“是”或“不是”)．

查看试题解析
12. 某地的温度T(℃)与海拔高度h(km)之间的关系如下所示：

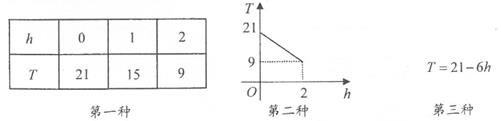
要算出海拔高度为6km时该地的温度，适宜用第种形式。

查看试题解析
13. 据测试：拧不紧的水龙头每分钟滴出100滴水，每滴水约 $0.05$ 毫升．小明同学洗手后，没有把水龙头拧紧，水龙头以测试的速度滴水，当小明离开 $x$ 分钟后，水龙头滴出 $y$ 毫升的水，则 $y$ 与 $x$ 之间的函数关系式是．

查看试题解析
14. 张大妈购进一批柚子，在集贸市场零售，已知卖出的柚子重量x（ $k g$ ）与售价y（元）之间的关系如下表：
重量x/ $k g$
1
2
3
4
…
售价y/元
$1.4$
$2.8$
$4.2$
$5.6$
…
根据表格中的数据，当卖出柚子的重量为6 $k g$ 时，售价为．

查看试题解析
15. 洲际弹道导弹的速度会随着时间的变化而变化．某种型号的洲际弹道导弹的速度 $v (k m / h)$ 与时间 $t (h)$ 之间的关系式为 $v = 1000 + 52 t$ ，则导弹发出后，第 $0.2 h$ 时的速度为 $k m / h$ ．

查看试题解析
16. 用一水管向某容器内持续注水，设单位时间内注入的水量保持不变；在注水过程中，表示容器内水深h与注水时间t的关系有如图所示的A，B，C，D四个图象，它们分别与E，F，G，H四种容器中的其中一种相对应，请你把相对应容器的字母填在下面的横线上.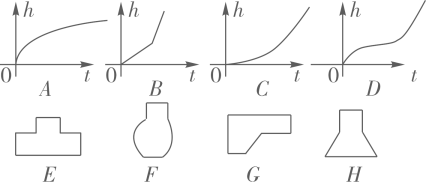

A→；B→；C→； D→.

查看试题解析

三、解答题（共8题，共67分）

17. 已知信件质量m(克)和邮资y(元)之间的关系如下表：

信件质量m/克

0<m≤20

20<m≤40

40<m≤60

邮资y/元

0.80

1.20

1.60

你能将其中一个变量看成另一个变量的函数吗？

查看试题解析
18. 小林同学在保养自己的山地自行车时发现，自行车每节链条的长度为 $2.5 c m$ ，交叉重叠部分的圆的直径为 $0.8 c m$ ．

(1)、观察图形填表：
链条节数（节）
2
3
6
链条长度（ $c m$ ）

(2)、如果 $x$ 节链条的总长度是 $y c m$ ，求 $y$ 与 $x$ 之间的关系式．

查看试题解析

19. 由于惯性的作用，行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”．为了测定某种型号小型载客汽车的刹车性能，车速不超过

140 k m / h

对这种型号的汽车进行了测试，测得的数据如下表：

刹车时车速 $v (k m / h)$	0	10	20	30	40	50	…
刹车距离 $s (m)$	0	$2.5$	5	$7.5$	10	$12.5$	…

请回答下列问题：

(1)、在这个变化过程中，自变量是，因变量是；

(2)、当刹车时车速为

30 k m / h

时，刹车距离是多少米？

(3)、观察表中数据可知，当刹车时车速每增加

10 k m / h

时，刹车距离增加多少米？该型号汽车某次的刹车距离为

20 m

，推测刹车时的车速是多少？

查看试题解析

20. 如图，梯形上底长是5，下底长是x，高是8．

(1)、写出梯形面积y与下底长x之间的关系式．

(2)、当 $x = 15$ 时，y等于多少．

查看试题解析
21. 在如图所示的三个函数图象中，有两个函数图象能近似地刻画如下a，b两个情境：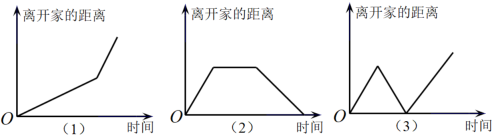
情境a：小芳离开家不久，发现把作业本忘在家里，于是返回家里找到了作业本再去学校；
情境b：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进．

(1)、情境a，b所对应的函数图象分别是，（填写序号）；

(2)、请你为剩下的函数图象写出一个适合的情境.

查看试题解析
22. “龟兔赛跑”的故事同学们都非常熟悉，图中的线段 $O D$ 和折线 $O A B C$ 表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．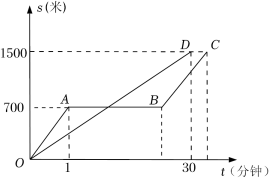

(1)、折线 $O A B C$ 表示赛跑过程中的路程与时间关系，线段 $O D$ 表示赛跑过程中的路程与时间的关系．（填“乌龟”和“兔子”）赛跑的全程是米．

(2)、兔子在起初每分钟跑多少米？乌龟每分钟爬多少米？

(3)、乌龟用了多少分钟追上了正在睡觉的兔子？

(4)、兔子醒来，以800米/分的速度跑向终点，结果还是比乌龟晚到了0.5分钟，请你算一算兔子中间停下睡觉用了多少分钟？

查看试题解析

23. 一辆汽车油箱内有油

56

升，从某地出发，每行驶

1

千米，耗油

0.08

升，如果设油箱内剩油量为

y (

升

)

，行驶路程为

x (

千米

)

，则

y

随

x

的变化而变化

(1)、在上述变化过程中，自变量是；因变量是．

(2)、用表格表示汽车从出发地行驶

100

千米、

200

千米、

300

千米、

400

千米时的剩油量．

请将表格补充完整：

行驶路程 $x ($ 千米 $)$	$100$	$200$	$300$	$400$
油箱内剩油量 $y ($ 升 $)$		$40$		$24$

(3)、试写出

y

与

x

的关系式．

(4)、这辆汽车行驶

350

千米时剩油多少升？汽车剩油

8

升时，行驶了多少千米？

查看试题解析

24. 如图，长方形 $A B C D$ 中， $B C = 8$ ， $C D = 5$ ，点E为边 $A D$ 上一动点，连接 $C E$ ，随着点E的运动，四边形 $A B C E$ 的面积也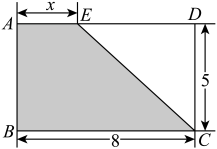发生变化．

(1)、写出四边形 $A B C E$ 的面积y与 $A E$ 的长 $x (0 < x < 8)$ 之间的关系式．

(2)、当四边形 $A B C E$ 的面积为25时，求 $D E$ 的长．

查看试题解析

物体的质量 $(k g)$	$0$	$1$	$2$	$3$	$4$	$5$
弹簧的长度 $(c m)$	$10$	$12.5$	$15$	$17.5$	$20$	$22.5$

信件质量m/克	0<m≤20	20<m≤40	40<m≤60
邮资y/元	0.80	1.20	1.60

重量x/ $k g$	1	2	3	4	…
售价y/元	$1.4$	$2.8$	$4.2$	$5.6$	…

链条节数（节）	2	3	6
链条长度（ $c m$ ）

2023年浙教版数学八年级上册5.2函数 同步测试（提高版）

一、选择题（每题3分，共30分）

二、填空题（第11题3分，12-16每题4分）

三、解答题（共8题，共67分）

2023年浙教版数学八年级上册5.2函数同步测试（提高版）