2023年浙教版数学八年级上册5.2函数 同步测试(基础版)
试卷更新日期:2023-10-03 类型:同步测试
一、选择题
-
1. 利用太阳能热水器加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题的因变量是( )A、太阳光强弱 B、水的温度 C、所晒时间 D、热水管2. 甲以每小时5km的速度行走,他所走的路程S(km)与行走时间t(h)之间的关系式为 , 其中自变量是( )A、S B、5 C、t D、S和t3. 下列变量间的关系,不是函数关系的是( )A、长方形的宽一定,其长与面积 B、正方形的面积与周长 C、等腰三角形的面积与底边长 D、圆的周长与半径4. 一个长方体木箱的长为 , 宽为 , 高为宽的2倍,则这个长方体的体积与宽之间的关系式为( )A、 B、 C、 D、5. 下列所述不属于函数关系的是( )A、长方形的面积一定,它的长和宽的关系 B、x+2与x的关系 C、匀速运动的火车,时间与路程的关系 D、某人的身高和体重的关系6. 一杯越晾越凉的水,下列能反映出水温与时间关系的图像是( )A、
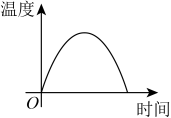 B、
B、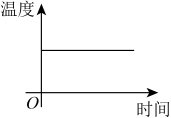 C、
C、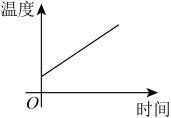 D、
D、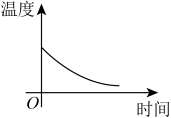 7. 下列图象中, 不是 的函数的是( )A、
7. 下列图象中, 不是 的函数的是( )A、 B、
B、 C、
C、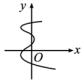 D、
D、 8. 下列关于变量x,y的关系,其中y不是x的函数的是( )A、
8. 下列关于变量x,y的关系,其中y不是x的函数的是( )A、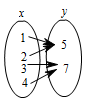 B、
B、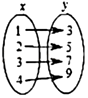 C、
C、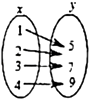 D、
D、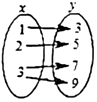 9. 在关系式中,当时,y的值为( )A、5 B、11 C、13 D、3010. 一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
9. 在关系式中,当时,y的值为( )A、5 B、11 C、13 D、3010. 一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:支撑物的高度
10
20
30
40
50
60
70
小车下滑的时间
4.23
3.00
2.45
2.13
1.89
1.71
1.59
下列说法正确的是( )
A、t是自变量,h是因变量 B、h每增加 , t减小1.23 C、随着h逐渐变大,t也逐渐变大 D、随着h逐渐升高,小车下滑的平均速度逐渐加快二、填空题(第11题5分,第12题3分,第13-16题每题4分)
-
11. 一般地,如果在某个过程中有两个x和y,并且对于变量x的每一个值,变量y都有的值与它对应,那么我们就称y是x的函数,其中x是 , y是12. 表示函数的三种方法是: , , .13. 若y=x2(x>0),则yx的函数;xy的函数.(填“是"或“不是")14. 函数自变量x的取值范围是.15. 已知一个梯形的面积为60,上底长是高的2倍,设高为x,下底为y,则y关于x的函数解析式为 .16. 在地球某地,地表以下岩层的温度与所处深度之间的关系可以近似地用表达式来表示(如图),当x的值为2时,相应的y值是 .

三、解答题(共8题,共66分)
-
17. 已知函数y= 中,当x=a时的函数值为1,试求a的值.18. 已知等腰三角形的周长为12,设腰长为x,底边长为y.(1)、试写出y关于x的函数表达式,并直接写出自变量x的取值范围.(2)、当x=5时,求出函数值.19. 已知一个长方形相邻的两边长分别是x和4 , 设长方形的周长为y .(1)、请写出y与x之间的关系式;(2)、当时,求长方形的周长;(3)、当长方形周长为30时,求x的值.20. 如图,圆柱的底面半径是1cm,圆柱的高由小到大变化,圆柱的侧面积随高的变化而变化.(结果保留π)
 (1)、在这个变化过程中,自变量和因变量各是什么?求圆柱的侧面积S( )与圆柱的高h(cm)之间的关系式;(2)、当圆柱的高为2cm时,圆柱的侧面积是多少?21. 某农场种植一种蔬菜,销售员张平根据往年的销售情况,对今年这种蔬菜的销售价格进行了预测,预测情况如图,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系.观察图象,你能得到关于这种蔬菜销售情况的哪些信息?答题要求:(1)请提供四条信息;(2)不必求函数的解析式.(注:此题答案不唯一,以上答案仅供参考.若有其它答案,只要是根据图象得出的信息,并且叙述正确都可以)
(1)、在这个变化过程中,自变量和因变量各是什么?求圆柱的侧面积S( )与圆柱的高h(cm)之间的关系式;(2)、当圆柱的高为2cm时,圆柱的侧面积是多少?21. 某农场种植一种蔬菜,销售员张平根据往年的销售情况,对今年这种蔬菜的销售价格进行了预测,预测情况如图,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系.观察图象,你能得到关于这种蔬菜销售情况的哪些信息?答题要求:(1)请提供四条信息;(2)不必求函数的解析式.(注:此题答案不唯一,以上答案仅供参考.若有其它答案,只要是根据图象得出的信息,并且叙述正确都可以)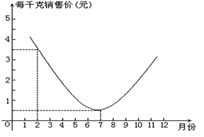 22. 地表以下岩层的温度/℃与所处深度/km有如下关系:
22. 地表以下岩层的温度/℃与所处深度/km有如下关系:深度/km
1
2
3
4
5
温度/℃
55
90
125
160
195
(1)、上表中自变量x是 , 因变量y是.(2)、请写出y与x的关系式.(3)、根据(2)中的关系式,估计地表以下7km处岩层的温度.23. 某通讯公司公布了收费标准,其中包月129元时,国内拨打电话超出部分0.15元/分.由于业务多,小明的爸爸打电话已超出了包月费.用x表示国内拨打超出时间,y表示国内拨打超出部分的电话费,下表是超出部分国内拨打的收费标准超出时间x/分
1
2
3
4
5
……
超出部分的电话费y/元
0.15
0.30
0.45
0.60
0.75
……
(1)、这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、如果国内拨打电话超出6分钟,那么超出部分的电话费是多少元?(3)、如果某次国内拨打电话超出部分的费用是1.2元,那么小明的爸爸国内拨打电话超出几分钟?24. 某文具店出售书包和文具盒,书包每个定价30元,文具盒每个定价5元.该店制定了两种优惠方案.方案1:买一个书包赠送一个文具盒;
方案2:按总价的9折(总价的90%)付款.
某班学生需购买8个书包,文具盒若干(不少于8个),如果设文具盒数为x(个),付款数为y(元).
(1)、分别求出两种优惠方案中y与x之间的关系式;(2)、购买文具盒多少个时两种方案付款相同;购买文具盒数大于8个时,两种方案中哪一种更省钱?