【备考2024】真题变式分层练:第12题—2023年高考数学全国乙卷(理科)
试卷更新日期:2023-10-02 类型:二轮复习
一、原题
-
1. 已知的半径为1,直线PA与相切于点A,直线PB与交于B,C两点,D为BC的中点,若 , 则的最大值为( )A、 B、 C、 D、
二、基础
-
2. 已知等边三角形ABC的边长为 , 则的值为( )A、 B、 C、 D、3. =(2,4)=(﹣1,1),则2﹣=( )A、(5,7) B、(5,9) C、(3,7) D、(3,9)4. 已知平面向量 , 满足 , 且 , 若 , 则( )A、 B、 C、 D、5. 如图,在圆中, , 点 , 在圆上, , 则的值为( )
 A、 B、 C、 D、6. 设点M是线段BC的中点,点A在线段BC外, , , 则( )A、8 B、4 C、2 D、17. 正方形的边长是2,是的中点,则( )A、 B、3 C、 D、58. 已知非零向量满足 , 则( )A、 B、1 C、 D、29. 已知平面向量与的夹角为 , , , 则的值为( )A、 B、2 C、4 D、10. 如图,是平行四边形所在平面内的一点,且满足 , 则( )
A、 B、 C、 D、6. 设点M是线段BC的中点,点A在线段BC外, , , 则( )A、8 B、4 C、2 D、17. 正方形的边长是2,是的中点,则( )A、 B、3 C、 D、58. 已知非零向量满足 , 则( )A、 B、1 C、 D、29. 已知平面向量与的夹角为 , , , 则的值为( )A、 B、2 C、4 D、10. 如图,是平行四边形所在平面内的一点,且满足 , 则( ) A、2 B、 C、 D、111. 如图,在中, , 则( )
A、2 B、 C、 D、111. 如图,在中, , 则( ) A、18 B、9 C、12 D、612. 平面向量与相互垂直,已知 , , 且与向量的夹角是钝角,则( )A、 B、 C、 D、
A、18 B、9 C、12 D、612. 平面向量与相互垂直,已知 , , 且与向量的夹角是钝角,则( )A、 B、 C、 D、三、提升
-
13. 折扇又名“纸扇”是一种用竹木或象牙做扇骨、韧纸或者绫绢做扇面的能折叠的扇子.某折扇如图1所示,其平面图为如图2所示的扇形AOB , 其半径为3, , 点E , F分别在 , 上,且 , 则的取值范围是( )
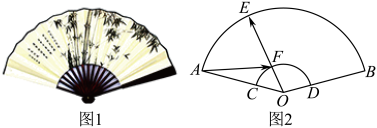 A、 B、 C、 D、14. 在中,是边的中点,且对于边上任意一点 , 恒有 , 则一定是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形15. 设非零向量满足 , 则在上的投影向量为( )A、 B、 C、 D、16. 已知直线与圆交于两点,若 , 其中为原点,则实数的值为( )A、1 B、 C、 D、217. 已知△ABC是单位圆O的内接三角形,若 , 则的最大值为( )A、 B、 C、1 D、18. 在△ABC中,已知 , , , D是边AB的中点,点E满足 , 则( )A、 B、-1 C、 D、19. 已知在三角形ABC中, , 点M,N分别为边AB,AC上的动点, , 其中 , 点P,Q分别为MN,BC的中点,则的最小值为( )A、 B、 C、 D、20. 已知向量的夹角为 , 且是函数的两个零点.若 , 则( )A、3 B、4 C、5 D、621. 已知单位向量 , , 若对任意实数 , 恒成立,则向量 , 的夹角的取值范围为( )A、 B、 C、 D、22. 如图,在等腰直角中,斜边 , 为线段BC上的动点,且 , 则的最小值为()
A、 B、 C、 D、14. 在中,是边的中点,且对于边上任意一点 , 恒有 , 则一定是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形15. 设非零向量满足 , 则在上的投影向量为( )A、 B、 C、 D、16. 已知直线与圆交于两点,若 , 其中为原点,则实数的值为( )A、1 B、 C、 D、217. 已知△ABC是单位圆O的内接三角形,若 , 则的最大值为( )A、 B、 C、1 D、18. 在△ABC中,已知 , , , D是边AB的中点,点E满足 , 则( )A、 B、-1 C、 D、19. 已知在三角形ABC中, , 点M,N分别为边AB,AC上的动点, , 其中 , 点P,Q分别为MN,BC的中点,则的最小值为( )A、 B、 C、 D、20. 已知向量的夹角为 , 且是函数的两个零点.若 , 则( )A、3 B、4 C、5 D、621. 已知单位向量 , , 若对任意实数 , 恒成立,则向量 , 的夹角的取值范围为( )A、 B、 C、 D、22. 如图,在等腰直角中,斜边 , 为线段BC上的动点,且 , 则的最小值为() A、 B、 C、4 D、623. 已知向量 , , 设 , 的夹角为 , 则( )A、 B、 C、 D、
A、 B、 C、4 D、623. 已知向量 , , 设 , 的夹角为 , 则( )A、 B、 C、 D、四、培优
-
24. 点为椭圆的右顶点,为椭圆上一点(不与重合),若(是坐标原点),则椭圆的离心率的取值范围是( )A、 B、 C、 D、25. 已知D为正三角形ABC中边BC的中点,E在线段AC上且 , 若AD与BE交于M,若 , 则正三角形ABC的边长为( )A、6 B、12 C、18 D、2426. 已知M,N是椭圆上关于原点O对称的两点,P是椭圆C上异于M,N的点,且的最大值是 , 则椭圆C的离心率是( )A、 B、 C、 D、27. 设点 , , 圆: , 点满足 , 设点的轨迹为 , 与交于点 , , 为直线上一点(为坐标原点),则( )A、4 B、 C、2 D、
-