【备考2024】真题变式分层练:第9题—2023年高考数学全国乙卷(理科)
试卷更新日期:2023-10-02 类型:二轮复习
一、原题
-
1. 已知为等腰直角三角形,AB为斜边,为等边三角形,若二面角为 , 则直线CD与平面ABC所成角的正切值为( )A、 B、 C、 D、
二、基础
-
2. 已知在三棱锥P-ABC中,PA=PB, ABC为锐角三角形,且点P在平面ABC上的投影O1为 ABC的垂心,O2为 PAB的重心.若二面角P-AB-C的余弦值为 ,且 , ,则CO2=( )A、 B、 C、3 D、13. 如图,长方体 中, , , , 分别为 , 上的动点, .点 在棱 上,且 ,若 平面 ,则二面角 的正切值为( )
 A、1 B、 C、 D、不确定4. 在正方体 中,点E为 的中点,则平面 与平面 夹角的余弦值为( )A、 B、 C、 D、5. 已知E,F分别是正方体ABCD﹣A1B1C1D1的棱BC,CC1的中点,则截面AEFD1与底面ABCD所成二面角的正弦值是( )
A、1 B、 C、 D、不确定4. 在正方体 中,点E为 的中点,则平面 与平面 夹角的余弦值为( )A、 B、 C、 D、5. 已知E,F分别是正方体ABCD﹣A1B1C1D1的棱BC,CC1的中点,则截面AEFD1与底面ABCD所成二面角的正弦值是( ) A、 B、 C、 D、6. 已知棱长为2的正方体 ,球 与该正方体的各个面相切,则平面 截此球所得的截面的面积为( )A、 B、 C、 D、7. 坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面是全等的等腰三角形.若 , 且等腰梯形所在的平面、等腰三角形所在的平面与平面的夹角的正切值均为 , 则该五面体的所有棱长之和为( )
A、 B、 C、 D、6. 已知棱长为2的正方体 ,球 与该正方体的各个面相切,则平面 截此球所得的截面的面积为( )A、 B、 C、 D、7. 坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面是全等的等腰三角形.若 , 且等腰梯形所在的平面、等腰三角形所在的平面与平面的夹角的正切值均为 , 则该五面体的所有棱长之和为( )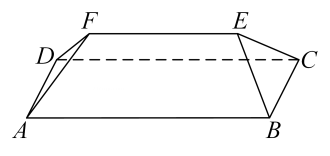 A、 B、 C、 D、8. 在长方体中, , 则二面角的余弦值为( )A、 B、 C、 D、9. 如图所示,是棱长为的正方体,、分别是棱、上的动点,且.当、、、共面时,平面与平面所成锐二面角的余弦值为( )
A、 B、 C、 D、8. 在长方体中, , 则二面角的余弦值为( )A、 B、 C、 D、9. 如图所示,是棱长为的正方体,、分别是棱、上的动点,且.当、、、共面时,平面与平面所成锐二面角的余弦值为( ) A、 B、 C、 D、10. 已知E,F分别是棱长为1的正方体ABCD-A1B1C1D1的棱BC,CC1的中点,则截面AEFD1与底面ABCD所成二面角的正弦值是()
A、 B、 C、 D、10. 已知E,F分别是棱长为1的正方体ABCD-A1B1C1D1的棱BC,CC1的中点,则截面AEFD1与底面ABCD所成二面角的正弦值是() A、 B、 C、 D、11. 在正方体中,下列几种说法不正确的是A、 B、B1C与BD所成的角为60° C、二面角的平面角为 D、与平面ABCD所成的角为12. 已知正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于( )A、 B、 C、 D、
A、 B、 C、 D、11. 在正方体中,下列几种说法不正确的是A、 B、B1C与BD所成的角为60° C、二面角的平面角为 D、与平面ABCD所成的角为12. 已知正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于( )A、 B、 C、 D、三、提升
-
13. 如图,在四棱锥中,平面ABCD, , , , 已知Q是四边形ABCD内部一点(包括边界),且二面角的平面角大小为 , 则面积的取值范围是( )
 A、 B、 C、 D、14. 二面角中, , , , , 且B、C为垂足, , , , , 则二面角大小为( )A、 B、 C、 D、15. 木升在古代多用来盛装粮食作物,是农家必备的用具,如图为一升制木升,某同学制作了一个高为40的正四棱台木升模型,已知该正四棱台的所有顶点都在一个半径为50的球O的球面上,且一个底而的中心与球O的球心重合,则该正四棱台的侧面与底面所成二面角的正弦值为( )
A、 B、 C、 D、14. 二面角中, , , , , 且B、C为垂足, , , , , 则二面角大小为( )A、 B、 C、 D、15. 木升在古代多用来盛装粮食作物,是农家必备的用具,如图为一升制木升,某同学制作了一个高为40的正四棱台木升模型,已知该正四棱台的所有顶点都在一个半径为50的球O的球面上,且一个底而的中心与球O的球心重合,则该正四棱台的侧面与底面所成二面角的正弦值为( ) A、 B、 C、 D、16. 已知正方体的棱长为1,点在线段上,有下列四个结论:
A、 B、 C、 D、16. 已知正方体的棱长为1,点在线段上,有下列四个结论:①;
②点到平面的距离为;
③二面角的余弦值为;
④若四面体的所有顶点均在球的球面上,则球的体积为.
其中所有正确结论的个数是( )
A、1 B、2 C、3 D、417. 如图是由边长为2的正与正方形拼接成的平面图形,现将沿折起,当二面角为时,直线与所成角的余弦值为( ) A、 B、 C、 D、18. 从空间一点向二面角分别作垂线为垂足.若 , 则该二面角的平面角的大小为( )A、60° B、120° C、60°或120° D、不确定19. 在矩形ABCD中,O为BD中点且 , 将平面ABD沿对角线BD翻折至二面角为90°,则直线AO与CD所成角余弦值为( )
A、 B、 C、 D、18. 从空间一点向二面角分别作垂线为垂足.若 , 则该二面角的平面角的大小为( )A、60° B、120° C、60°或120° D、不确定19. 在矩形ABCD中,O为BD中点且 , 将平面ABD沿对角线BD翻折至二面角为90°,则直线AO与CD所成角余弦值为( ) A、 B、 C、 D、20. 已知在正方体中,点E为棱BC的中点,直线在平面A1B1C1D1内.若二面角的平面角为 , 则的最小值为( )A、 B、 C、 D、21. 如图,已知正三棱柱 ,E,F分别是棱 上的点.记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( )
A、 B、 C、 D、20. 已知在正方体中,点E为棱BC的中点,直线在平面A1B1C1D1内.若二面角的平面角为 , 则的最小值为( )A、 B、 C、 D、21. 如图,已知正三棱柱 ,E,F分别是棱 上的点.记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( ) A、 B、 C、 D、
A、 B、 C、 D、四、培优
-
22. 将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,有如下四个结论:

①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD所成的角为60°;
④AB与CD所成的角为60°.
其中错误的结论是( )
A、① B、② C、③ D、④23. 已知点M是棱长为4的正方体的棱的中点.过直线作平面 , 记平面与棱的交点为K,当平面与底面所成的锐二面角最小时,( ) A、3 B、 C、 D、124. 已知边长为1的等边三角形 与正方形 有一公共边 ,二面角 的余弦值为 ,若A、B、C、D、E在同一球面上,则此球的体积为( )A、2π B、 C、 D、25. 如图,在四棱锥中,底面为矩形,是等边三角形,平面底面 , , 四棱锥的体积为 , 为的中点.
A、3 B、 C、 D、124. 已知边长为1的等边三角形 与正方形 有一公共边 ,二面角 的余弦值为 ,若A、B、C、D、E在同一球面上,则此球的体积为( )A、2π B、 C、 D、25. 如图,在四棱锥中,底面为矩形,是等边三角形,平面底面 , , 四棱锥的体积为 , 为的中点. (1)、线段的长是( )A、3 B、 C、 D、6(2)、平面与平面所成二面角的正切值是( )A、2 B、 C、 D、1(3)、直线与平面所成角的正弦值是( )A、 B、 C、 D、
(1)、线段的长是( )A、3 B、 C、 D、6(2)、平面与平面所成二面角的正切值是( )A、2 B、 C、 D、1(3)、直线与平面所成角的正弦值是( )A、 B、 C、 D、
-
