【备考2024】真题变式分层练:第8题—2023年高考数学全国乙卷(理科)
试卷更新日期:2023-10-02 类型:二轮复习
一、原题
-
1. 已知圆锥PO的底面半径为 , O为底面圆心,PA,PB为圆锥的母线, , 若的面积等于 , 则该圆锥的体积为( )A、 B、 C、 D、
二、基础
-
2. “抽陀螺”是中国传统民俗体育游戏,陀螺上大下尖,将尖头着地,以绳绕之,然后抽打,使其旋转.如图所示的陀螺近似看作由一个圆锥与一个圆柱组成的组合体,其中圆柱的底面直径为2,圆锥与圆柱的高都为1,则该几何体的表面积为( )
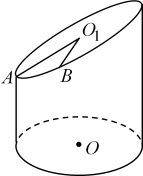
 A、 B、 C、 D、3. 一个内壁底面半径为2的圆柱体玻璃杯中盛有体积为V的水,若放入一个玻璃球(球的半径与圆柱体玻璃杯内壁的底面半径相同)后,水恰好淹没了玻璃球,则V=( )A、 B、6π C、 D、8π4. 已知在四边形中, , , 且 , , 则将四边形绕直线旋转一周后所形成的几何体的侧面积为( )A、 B、 C、 D、5. 已知圆锥SA的轴截面是边长为的等边三角形,顶点S和底面圆周上的所有点都在球O的球面上,则球O的体积为( )A、 B、 C、 D、6. 已知等腰直角三角形的斜边长为 , 以直角边所在直线为轴,其余两边旋转一周形成的面围成一个几何体,这个几何体的表面积为( )A、 B、 C、 D、7. 已知表面积为的圆锥的侧面展开图是一个半圆,则圆锥的底面半径为( )A、3 B、 C、6 D、8. 九章算术卷商功记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺.问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一”就是说:圆堡瑽圆柱体的体积为底面圆的周长的平方高 , 则由此可推得圆周率的取值为( )A、 B、 C、 D、9. 已知圆锥的底面半径为 , 其侧面展开图为一个半圆,则该圆锥的母线长为( )A、 B、 C、 D、10. 已知一个圆锥的母线长为2,其侧面积为 , 则该圆锥的高为( )A、1 B、 C、 D、211. 如图,某圆柱体的高为是该圆柱体的轴截面.已知从点出发沿着圆柱体的侧面到点的路径中,最短路径的长度为 , 则该圆柱体的体积是( )
A、 B、 C、 D、3. 一个内壁底面半径为2的圆柱体玻璃杯中盛有体积为V的水,若放入一个玻璃球(球的半径与圆柱体玻璃杯内壁的底面半径相同)后,水恰好淹没了玻璃球,则V=( )A、 B、6π C、 D、8π4. 已知在四边形中, , , 且 , , 则将四边形绕直线旋转一周后所形成的几何体的侧面积为( )A、 B、 C、 D、5. 已知圆锥SA的轴截面是边长为的等边三角形,顶点S和底面圆周上的所有点都在球O的球面上,则球O的体积为( )A、 B、 C、 D、6. 已知等腰直角三角形的斜边长为 , 以直角边所在直线为轴,其余两边旋转一周形成的面围成一个几何体,这个几何体的表面积为( )A、 B、 C、 D、7. 已知表面积为的圆锥的侧面展开图是一个半圆,则圆锥的底面半径为( )A、3 B、 C、6 D、8. 九章算术卷商功记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺.问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一”就是说:圆堡瑽圆柱体的体积为底面圆的周长的平方高 , 则由此可推得圆周率的取值为( )A、 B、 C、 D、9. 已知圆锥的底面半径为 , 其侧面展开图为一个半圆,则该圆锥的母线长为( )A、 B、 C、 D、10. 已知一个圆锥的母线长为2,其侧面积为 , 则该圆锥的高为( )A、1 B、 C、 D、211. 如图,某圆柱体的高为是该圆柱体的轴截面.已知从点出发沿着圆柱体的侧面到点的路径中,最短路径的长度为 , 则该圆柱体的体积是( ) A、3 B、 C、 D、12. 灯罩的更新换代比较快,而且灯具大部分都是设计师精心设计,对于灯来说,不用将灯整个都换掉,只需要把灯具的外部灯罩进行替换就可以改变灯的风格.杰斯决定更换卧室内的两个灯罩来换换氛围,已知该灯罩呈圆台结构,上下底皆挖空,上底半径为10 , 下底半径为18 , 母线长为17 , 侧面计划选用丝绸材质布料制作,若不计做工布料的浪费,则更换两个灯罩需要的丝绸材质布料面积为( )
A、3 B、 C、 D、12. 灯罩的更新换代比较快,而且灯具大部分都是设计师精心设计,对于灯来说,不用将灯整个都换掉,只需要把灯具的外部灯罩进行替换就可以改变灯的风格.杰斯决定更换卧室内的两个灯罩来换换氛围,已知该灯罩呈圆台结构,上下底皆挖空,上底半径为10 , 下底半径为18 , 母线长为17 , 侧面计划选用丝绸材质布料制作,若不计做工布料的浪费,则更换两个灯罩需要的丝绸材质布料面积为( ) A、 B、 C、 D、13. 石碾子是我国传统粮食加工工具,如图是石碾子的实物图,石碾子主要由碾盘、碾滚(圆柱形)和碾架组成.碾盘中心设竖轴(碾柱),连碾架,架中装碾滚,以人推或畜拉的方式,通过碾滚在碾盘上的滚动达到碾轧加工粮食作物的目的.若推动拉杆绕碾盘转动2周,碾滚的外边缘恰好滚动了5圈,碾滚与碾柱间的距离忽略不计,则该圆柱形碾滚的高与其底面圆的直径之比约为( )
A、 B、 C、 D、13. 石碾子是我国传统粮食加工工具,如图是石碾子的实物图,石碾子主要由碾盘、碾滚(圆柱形)和碾架组成.碾盘中心设竖轴(碾柱),连碾架,架中装碾滚,以人推或畜拉的方式,通过碾滚在碾盘上的滚动达到碾轧加工粮食作物的目的.若推动拉杆绕碾盘转动2周,碾滚的外边缘恰好滚动了5圈,碾滚与碾柱间的距离忽略不计,则该圆柱形碾滚的高与其底面圆的直径之比约为( ) A、3:2 B、5:4 C、5:3 D、4:3
A、3:2 B、5:4 C、5:3 D、4:3三、提升
-
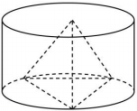
14. 圆台的上、下底面半径分别是10和20,它的侧面展开图扇环的圆心角为180°,则下面说法不正确的是( )A、圆台的母线长是20 B、圆台的表面积是 C、圆台的高是 D、圆台的体积是15. 已知圆锥的顶点为 , 底面圆心为 , 为底面直径, , , 点在底面圆周上,且二面角为 , 则下列各选项正确的是( )A、该圆锥的体积为 B、该圆锥的侧面积为 C、 D、过圆锥任意两条母线的截面中面积最大的为16. 已知母线长为a的圆锥的侧面展开图为半圆,在该圆锥内放置一个圆柱,则当圆柱的侧面积最大时,圆柱的体积为( )A、 B、 C、 D、17. 一个圆台的侧面展开图是半圆面所在的扇环,两个半圆半径分别为2和4,则该圆台的体积是( )A、 B、 C、 D、18. 阿基米德是伟大的古希腊数学家,他和高斯、牛顿并列为世界三大数学家,他一生最为满意的一个数学发现就是“圆柱容球”定理,即圆柱容器里放了一个球,该球顶天立地,四周碰边(即球与圆柱形容器的底面和侧面都相切),球的体积是圆柱体积的三分之二,球的表面积也是圆柱表面积的三分之二.今有一“圆柱容球”模型,其圆柱表面积为 , 则该模型中圆柱的体积与球的体积之和为( )A、 B、 C、 D、19. 如图,四面体各个面都是边长为1的正三角形,其三个顶点在一个圆柱的下底面圆周上,另一个顶点是上底面圆心,圆柱的侧面积是( )
 A、 B、 C、 D、20. 圆锥的母线长为4,侧面积是底面积的倍,过圆锥的两条母线作圆锥的截面,则该截面面积的最大值是( )A、8 B、 C、 D、21. 设圆柱的体积为 , 当其表面积最小时,圆柱的母线长为( )A、 B、 C、 D、22. 现有一个轴截面是边长为4的等边三角形的倒置圆锥(顶点在下方,底面在上方),将半径为的小球放入圆锥,使得小球与圆锥的侧面相切,过所有切点所在平面将圆锥分割成两个部分,则分割得到的圆台的侧面积为( )A、 B、 C、 D、23. 已知圆锥的底面半径为2,高为4,一个圆柱的下底面在圆锥的底面上,上底面的圆周在圆锥的侧面上,当圆柱侧面积为4π时该圆柱的体积为( )A、π B、2π C、3π D、4π
A、 B、 C、 D、20. 圆锥的母线长为4,侧面积是底面积的倍,过圆锥的两条母线作圆锥的截面,则该截面面积的最大值是( )A、8 B、 C、 D、21. 设圆柱的体积为 , 当其表面积最小时,圆柱的母线长为( )A、 B、 C、 D、22. 现有一个轴截面是边长为4的等边三角形的倒置圆锥(顶点在下方,底面在上方),将半径为的小球放入圆锥,使得小球与圆锥的侧面相切,过所有切点所在平面将圆锥分割成两个部分,则分割得到的圆台的侧面积为( )A、 B、 C、 D、23. 已知圆锥的底面半径为2,高为4,一个圆柱的下底面在圆锥的底面上,上底面的圆周在圆锥的侧面上,当圆柱侧面积为4π时该圆柱的体积为( )A、π B、2π C、3π D、4π四、培优
-
24. 在中,内角A,B,C所对的边分别为 , , , 将该三角形绕AC边旋转360°得一个旋转体,则该旋转体体积为( )A、 B、 C、 D、25. 《几何原本》是古希腊数学家欧几里得的一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.如图,若都是直角圆锥底面圆的直径,且 , 则异面直线与所成角的余弦值为( )
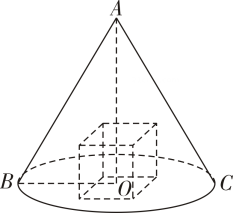
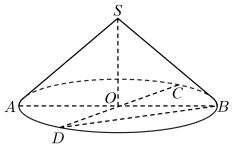 A、 B、 C、 D、26. 21世纪以来,中国钢铁工业进入快速发展阶段,某工厂要加工一种如图所示的圆锥体容器,圆锥的高和母线长分别为和 , 该容器需要在圆锥内部挖出一个正方体槽,则可以挖出的正方体的最大棱长为( )
A、 B、 C、 D、26. 21世纪以来,中国钢铁工业进入快速发展阶段,某工厂要加工一种如图所示的圆锥体容器,圆锥的高和母线长分别为和 , 该容器需要在圆锥内部挖出一个正方体槽,则可以挖出的正方体的最大棱长为( )
 A、 B、 C、 D、27. 最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》(1247年).该书第二章为“天时类”,收录了有关降水量计算的四个例子,分别是“天池测雨”、“圆罂测雨”“峻积验雪”和“竹器验雪”.如图“圆罂测雨”法是下雨时用一个由上下两个等高的圆台吻合而成的圆罂器皿收集雨水,已知数据如图(注:1尺=10寸),平地的降雨量的近似值是( )
A、 B、 C、 D、27. 最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》(1247年).该书第二章为“天时类”,收录了有关降水量计算的四个例子,分别是“天池测雨”、“圆罂测雨”“峻积验雪”和“竹器验雪”.如图“圆罂测雨”法是下雨时用一个由上下两个等高的圆台吻合而成的圆罂器皿收集雨水,已知数据如图(注:1尺=10寸),平地的降雨量的近似值是( )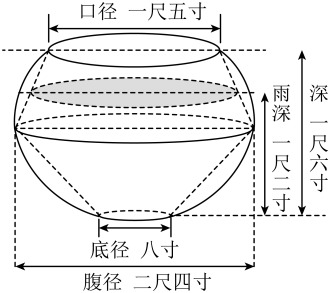
注意: ,
A、6寸 B、9寸 C、12寸 D、18寸28. 在五面体中,底面为矩形, , 和均为等边三角形, , , 则该五面体的外接球的半径为( )A、 B、 C、 D、
-