【备考2024】真题变式分层练：第5题—2023年高考数学全国乙卷（理科）

试卷更新日期：2023-09-30 类型：二轮复习

进入出卷网下载

一、原题

1. 设O为平面坐标系的坐标原点，在区域 ${(x ， y) | 1 \leq x^{2} + y^{2} \leq 4}$ 内随机取一点，记该点为A，则直线OA的倾斜角不大于 $\frac{π}{4}$ 的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析

二、基础

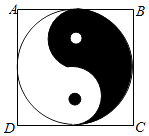
2. 在区间(0, $\frac{1}{2}$ )随机取1个数，则取到的数小于 $\frac{1}{3}$ 的概率为（）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
3. 在区间 $(- 2 ， 6)$ 内随机取一个数x，使得不等式 $9^{x} - 10 \times 3^{x} + 9 < 0$ 成立的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
4.
如图，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是（　　）

A、 $\frac{1}{4}$ B、 $\frac{π}{8}$ C、 $\frac{1}{2}$ D、 $\frac{π}{4}$

查看试题解析
5. 某人午觉醒来，发现表停了，他打开收音机，想听电台整点报时，则他等待时间不多于 $30$ 分钟的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
6. 已知 $Ω = {(x ， y) | x^{2} + y^{2} < 1}$ ，在 $Ω$ 中任取一点 $P (x ， y)$ ，则事件“ $| x | + | y | < 1$ ”发生的概率为（）

A、 $\frac{1}{2}$ B、 $1 - \frac{2}{π}$ C、 $\frac{2}{π}$ D、 $\frac{π}{2} - 1$

查看试题解析
7. 在射击比赛中，甲乙两人对同一目标各进行一次射击，甲击中目标的概率为 $\frac{3}{5}$ ，乙击中目标的概率为 $\frac{4}{5}$ ，在目标被击中的情况下，甲击中目标的概率为（）

A、 $\frac{3}{4}$ B、 $\frac{12}{25}$ C、 $\frac{15}{23}$ D、 $\frac{3}{7}$

查看试题解析
8. 在区间 $[- 2 ， 5]$ 上随机地抽取一个实数x，则x满足 $x^{2} < 4$ 的概率为（）

A、 $\frac{2}{7}$ B、 $\frac{3}{7}$ C、 $\frac{4}{7}$ D、 $\frac{5}{7}$

查看试题解析
9. 有诗云：“芍药乘春宠，何曾羡牡丹.”芍药不仅观赏性强，且具有药用价值.某地打造了以芍药为主的花海大世界.其中一片花海是正方形，它的四个角的白色部分都是以正方形的顶点为圆心､正方形边长的一半为半径的圆弧与正方形的边所围成的（如图所示）.白色部分种植白芍，中间阴影部分种植红芍.倘若你置身此正方形花海之中，则恰好处在红芍中的概率是（）

A、 $1 - \frac{π}{4}$ B、 $\frac{π}{4} - \frac{1}{2}$ C、 $\frac{π}{2} - 1$ D、 $\frac{π}{4}$

查看试题解析
10. 右图是一张“春到福来”的剪纸窗花，为了估计深色区域的面积，将窗花图案放置在边长为 $20 c m$ 的正方形内，在该正方形内随机生成1000个点，恰有535个点落在深色区域内，则此窗花图案中深色区域的面积约为（）

A、 $168 c m^{2}$ B、 $214 c m^{2}$ C、 $248 c m^{2}$ D、 $336 c m^{2}$

查看试题解析

三、提升

11. 如图，已知线段AD的长为3，B，C是线段AD上的两点，则线段AB，BC，CD能构成三角形的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
12. 下图来自古希腊数学家希波克拉底所研究的几何图形，此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC.△ABC的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ，在整个图形中随机取一点，此点取自Ⅰ、Ⅱ、Ⅲ的概率分别记为 $p_{1} ， p_{2} ， p_{3}$ ，则（）

A、 $p_{1} = p_{2}$ B、 $p_{1} = p_{3}$ C、 $p_{2} = p_{3}$ D、 $p_{1} = p_{2} + p_{3}$

查看试题解析
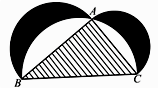13. 甲、乙两人约定某日上午在 $M$ 地见面，若甲是7点到8点开始随机到达，乙是7点30分到8点30分随机到达，约定，先到者没有见到对方时等候10分钟，则甲、乙两人能见面的概率为（）.

A、 $\frac{1}{3}$ B、 $\frac{1}{6}$ C、 $\frac{5}{9}$ D、 $\frac{3}{8}$

查看试题解析
14. 设某医院仓库中有10盒同样规格的 $X$ 光片，已知其中有5盒、3盒、2盒依次是甲厂、乙厂、丙厂生产的．且甲、乙、丙三厂生产该种 $X$ 光片的次品率依次为 $\frac{1}{10}$ ， $\frac{1}{15}$ ， $\frac{1}{20}$ ，现从这10盒中任取一盒，再从这盒中任取一张 $X$ 光片，则取得的 $X$ 光片是次品的概率为（）

A、0.08 B、0.1 C、0.15 D、0.2

查看试题解析
15. 对图中的A、B、C、D四个区域染色，每块区域染一种颜色，有公共边的区域不同色，

A

B

C

D

现有红、黄、蓝三种不同颜色可以选择，则不同的染色方法共有（　　）

A、12种 B、18种 C、20 D、22种

查看试题解析
16. 设O为平面坐标系的坐标原点，在区域 ${(x ， y) | 1 \leq x^{2} + y^{2} \leq 4}$ 内随机取一点A，则直线OA的倾斜角不大于 $\frac{π}{4}$ 的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
17. 在崂山的山脚下临海断崖南侧，距岸百米处有一座石柱，形如老人坐在碧波之中，人称“石老人”.老人以手托腮，注目凝神，每天晨迎旭日，暮送晚霞，伴着潮起潮落，历尽沧桑，不知度过了多少岁月.这个由大自然鬼斧神工雕凿的艺术杰作，已成为石老人国家旅游度假区的重要标志，若该景区在开放时间内，每半个小时会有一趟观光车从景区入口发车，有一名学生周日上午某时刻到达景区入口，准备乘坐观光车，则他等待时间不多于10分钟的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{1}{3}$

查看试题解析
18. 赵爽是我国古代著名数学之家，他用于证明勾股定理的“赵爽弦图”是由四个全等的直角三角形和一个小四边形A₁B₁C₁D₁构成，如图所示．已知直角三角形的两条直角边长分别为3，4，若在“赵爽弦图”中随机取一点，则该点取自四边形A₁B₁C₁D₁区域内的概率为（）

A、 $\frac{9}{25}$ B、 $\frac{1}{25}$ C、 $\frac{16}{25}$ D、 $\frac{4}{25}$

查看试题解析
19. 《九章算术》是我国古典数学教学名著之一，书中有如下问题：“今有勾五步，股十二步，问勾中容方几何？”其意思为“已知直角三角形两直角边长分别为5步和12步，问一边在勾上的内接正方形的边长为多少步？”在此题的条件下，向此三角形内随机投289粒豆子，则落在这个内接正方形内的豆子数大约是（）

A、90粒 B、120粒. C、180粒 D、240粒

查看试题解析
20. 如图，点 $C$ 在以 $A B$ 为直径的圆上，且满足 $C A = C B$ ，圆内的弧线是以 $C$ 为圆心， $C A$ 为半径的圆的一部分.记 $Δ A B C$ 三边所围成的区域（灰色部分）为Ⅰ，右侧月牙形区域（黑色部分）为Ⅱ.在整个图形中随机取一点，记此点取自Ⅰ，Ⅱ的概率分别为 $P_{1}$ ， $P_{2}$ ，则（）

A、 $P_{1} = P_{2}$ B、 $P_{1} > P_{2}$ C、 $P_{1} + P_{2} = \frac{4}{π + 1}$ D、 $P_{2} - P_{1} = \frac{1}{π + 1}$

查看试题解析

四、培优

21. 如图来自古希腊数学家希波克拉底所研究的几何图形．此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC．△ABC的三边所围成的区域记为I，黑色部分记为II，其余部分记为III．在整个图形中随机取一点，此点取自I，II，III的概率分别记为p₁ ， p₂ ， p₃ ，则

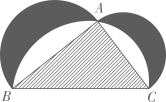A、p₁=p₂ B、p₁=p₃ C、p₂=p₃ D、p₁=p₂+p₃

查看试题解析
22. 若非负数x，y满足 ${\begin{array}{l} | x - y | \leq 1 \\ x + y \leq 3 \end{array}$ ，则事件“ $2 x + y \geq 4$ ”发生的概率为（）

A、 $\frac{2}{15}$ B、 $\frac{\sqrt{2}}{15}$ C、 $\frac{2}{5}$ D、 $\frac{\sqrt{2}}{5}$

查看试题解析
23. 如图所示，阴影部分由四个全等的三角形组成，每个三角形是腰长等于圆的半径，顶角为 $θ (0 < θ < \frac{π}{2})$ 的等腰三角形．如果在圆内随机取一点，那么该点落到阴影部分内的概率为 $\frac{1}{π}$ ，则 $θ =$ （）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{5 π}{12}$

查看试题解析
24. 如图，E是正方形ABCD内一动点，且满足 $A E ⊥ B E$ ，在正方形ABCD内随机投一个点，则该点落在图中阴影部分的概率的最小值是（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4} - \frac{\sqrt{2}}{4}$ C、 $\frac{1}{8} + \frac{\sqrt{2}}{8}$ D、 $\frac{5}{8} - \frac{\sqrt{3}}{8}$

查看试题解析
25. 剪纸艺术是中国传统的民间工艺，已成为世界艺术宝库中的一种珍藏．其特点主要表现在空间观念的二维性．在小学实验课本中，有这样一幅图例(如图所示)，矩形ABCD满足 $B C = 2 \sqrt{3} A B$ ， E为BC的中点，其中曲线为过A、D、E三点的圆弧，若随机向矩形内投一点，则该点落在阴影部分的概率为（）

A、 $\frac{2 \sqrt{3} π}{9} - 1$ B、 $1 - \frac{\sqrt{3} π}{9}$ C、 $\sqrt{3} - \frac{π}{2}$ D、 $\frac{π}{4} - \frac{1}{2}$

查看试题解析
26. 2021年是中国共产党百年华诞，3月24日，中宣部发布中国共产党成立100周年庆祝活动标识(图1)，标识由党徽､数字“100”“1921”“2021”和56根光芒线组成，生动展现中国共产党团结带领中国人民不忘初心､牢记使命､艰苦奋斗的百年光辉历程.其中“100”的两个“0”设计为两个半径为 $R$ 的相交大圆，分别内含一个半径为 $r$ 的同心小圆，且同心小圆均与另一个大圆外切(图2).已知 $R = (\sqrt{2} + 1) r$ ，则在两个大圆的区域内随机取一点，则该点取自两大圆公共部分的概率为（）

A、 $\frac{π - 1}{2 π + 1}$ B、 $\frac{π - 2}{3 π + 2}$ C、 $\frac{π - 3}{4 π + 3}$ D、 $\frac{4 - π}{5 π + 4}$

查看试题解析
27. 在圆 $(x - 2)^{2} ＋ (y - 2)^{2} ＝ 4$ 内任取一点，则该点恰好在区域 ${\begin{array}{l} x + 2 y - 5 \geq 0 \\ x - 2 y + 3 \geq 0 \\ x \leq 3 \end{array}$ 内的概率为（）

A、 $\frac{1}{8 π}$ B、 $\frac{1}{4 π}$ C、 $\frac{1}{2 π}$ D、 $\frac{1}{π}$

查看试题解析
28. 2018年平昌冬季奥运会于2月9日~2月25日举行，为了解奥运会五环所占面积与单独五个环面积和的比例P，某学生设计了如下的计算机模拟，通过计算机模拟长为8，宽为5的长方形内随机取了N个点，经统计落入五环及其内部的点数为 $n$ ，圆环半径为1，如图，则比值 $P$ 的近似值为（）

A、 $\frac{32 n}{5 π N}$ B、 $\frac{32 n}{π N}$ C、 $\frac{8 n}{π N}$ D、 $\frac{5 π n}{32 N}$

查看试题解析