【备考2024】真题变式分层练：第3题—2023年高考数学全国乙卷（理科）

试卷更新日期：2023-09-30 类型：二轮复习

进入出卷网下载

一、原题

1. 如图，网格纸上绘制的一个零件的三视图，网格小正方形的边长为1，则该零件的表面积为（）

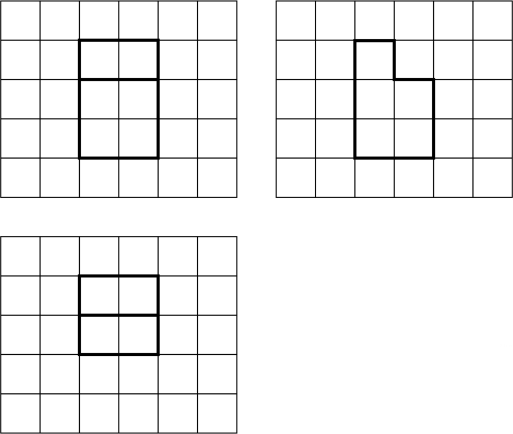A、24 B、26 C、28 D、30

查看试题解析

二、基础

2. 某几何体的三视图如图所示，则该几何体的体积为（）

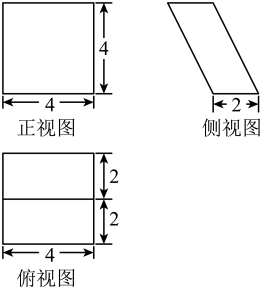A、 $\frac{32}{3}$ B、8 C、32 D、 $16 \sqrt{2}$

查看试题解析
3. 某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位： $c m^{3}$ ）是（）

A、6 B、 $\frac{20}{3}$ C、 $\frac{22}{3}$ D、 $\frac{23}{3}$

查看试题解析
4. 某几何体的三视图如图所示，则该几何体的体积是（）

A、 $π + 4$ B、 $2 π + 4$ C、 $π + \frac{8}{3}$ D、 $2 π + \frac{8}{3}$

查看试题解析
5. 某几何体的三视图如图所示，则该几何体的表面积是（）

A、14 B、20 C、 $10 + 2 \sqrt{5}$ D、 $16 + 2 \sqrt{5}$

查看试题解析
6. “抽陀螺”是中国传统民俗体育游戏，陀螺上大下尖，将尖头着地，以绳绕之，然后抽打，使其旋转．如图所示的陀螺近似看作由一个圆锥与一个圆柱组成的组合体，其中圆柱的底面直径为2，圆锥与圆柱的高都为1，则该几何体的表面积为（）

A、 $4 π$ B、 $(3 + \sqrt{2}) π$ C、 $(2 + \sqrt{2}) π$ D、 $(8 + 2 \sqrt{5}) π$

查看试题解析
7. 一个内壁底面半径为2的圆柱体玻璃杯中盛有体积为V的水，若放入一个玻璃球(球的半径与圆柱体玻璃杯内壁的底面半径相同)后，水恰好淹没了玻璃球，则V=（）

A、 $\frac{20 π}{3}$ B、6π C、 $\frac{16 π}{3}$ D、8π

查看试题解析
8. 已知圆锥SA的轴截面是边长为 $2 \sqrt{3}$ 的等边三角形，顶点S和底面圆周上的所有点都在球O的球面上，则球O的体积为（）

A、 $4 \sqrt{3} π$ B、 $\frac{32}{3} π$ C、 $\frac{20 \sqrt{5}}{3} π$ D、 $\frac{28 \sqrt{7}}{3} π$

查看试题解析
9. 通用技术结业课程上，老师带领大家设计一个圆台状的器皿材料的厚度忽略不计，该器皿下底面半径为3cm，上底面半径为18cm，容积为 $1935 \sqrt{3} π c m^{3}$ ，则该器皿的高为（）

A、 $5 \sqrt{3} c m$ B、 $12 \sqrt{3} c m$ C、 $15 \sqrt{3} c m$ D、 $20 \sqrt{3} c m$

查看试题解析
10. 一个四棱锥的三视图如图所示，则该几何体的体积为（）

A、8 B、 $\frac{8}{3}$ C、 $\frac{4}{3}$ D、 $\frac{32}{3}$

查看试题解析
11. 某一棱锥的三视图如图所示，则其侧面积为（）

A、 $8 + 4 \sqrt{13}$ B、20 C、 $12 \sqrt{2} + 4 \sqrt{13}$ D、 $8 + 12 \sqrt{2}$

查看试题解析
12. 一个圆柱形粮仓，高1丈3尺 $3 \frac{1}{3}$ 寸，可容纳米2000斛，已知1丈 $= 10$ 尺 $= 100$ 寸，1斛米 $= 1620$ 立方寸，若 $π$ 取3，则该圆柱形粮仓底面的周长是（）

A、440寸 B、540寸 C、560寸 D、640寸

查看试题解析

三、提升

13. 攒尖是我国古代建筑中屋顶的一种结构形式，宋代称为最尖，清代称攒尖，通常有圆形攒尖､三角攒尖､四角攒尖､八角攒尖，也有单檐和重檐之分，多见于亭阁式建筑､园林建筑.下面以四角攒尖为例，如图，它的屋顶部分的轮廓可近似看作一个正四棱锥.已知正四棱锥的底面边长为 $3 \sqrt{2}$ 米，侧棱长为5米，则其体积为（）立方米.

A、 $24 \sqrt{2}$ B、24 C、 $72 \sqrt{2}$ D、72

查看试题解析
14. 某几何体的三视图如图所示（单位： $c m$ ），则该几何体的体积是（）

A、 $1 c m^{3}$ B、 $\frac{2}{3} c m^{3}$ C、 $\frac{3}{2} c m^{3}$ D、 $\frac{16}{3} c m^{3}$

查看试题解析
15. 如图是某个四面体的三视图，若在该四面体内任取一点P，则点P落在该四面体内切球内部的概率为（）

A、 $\frac{\sqrt{2}}{9 π}$ B、 $\frac{\sqrt{6} π}{18}$ C、 $\frac{3 \sqrt{2} π}{16}$ D、 $\frac{π}{16}$

查看试题解析
16. 刘徽（225—295）是我国魏晋时期杰出的数学家，擅长利用切割的方法求几何体的体积.他将底面是直角三角形的直三棱柱称为“堑堵”，将底面为矩形且一条侧棱垂直于底面的四棱锥称为“阳马”.已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示，则该几何体的体积是（）

A、 $\frac{20}{3}$ B、 $\frac{32}{3}$ C、 $\frac{16}{3}$ D、 $\frac{26}{3}$

查看试题解析
17. 某几何体的三视图如图所示，则该几何体的体积是（）

A、18 B、36 C、54 D、108

查看试题解析
18. 已知某几何体的三视图如图所示，则该几何体的表面积是（）

A、4 B、 $6 + 2 \sqrt{5}$ C、 $2 + 2 \sqrt{5}$ D、6

查看试题解析
19. 在三棱锥 $V - A B C$ 中， $V A ， V B ， V C$ 两两垂直， $V A = V B = V C = 1$ ，则点 $V$ 到平面 $A B C$ 的距离等于（）

A、1 B、 $\frac{1}{2}$ C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
20. 如图，在棱长均为 $2$ 的直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $D$ 是 $A_{1} B_{1}$ 的中点，过 $B$ 、 $C$ 、 $D$ 三点的平面将该三棱柱截成两部分，则顶点 $B_{1}$ 所在部分的体积为（）

A、 $\frac{2 \sqrt{3}}{3}$ B、 $\frac{5 \sqrt{3}}{6}$ C、 $\sqrt{3}$ D、 $\frac{7 \sqrt{3}}{6}$

查看试题解析
21. 在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑.在鳖臑 $A - B C D$ 中， $A B ⊥$ 平面 $B C D$ ， $B C ⊥ C D$ ，且 $A B = B C = C D = 1$ ，则其内切球表面积为（）

A、 $3 π$ B、 $\sqrt{3} π$ C、 $(3 - 2 \sqrt{2}) π$ D、 $(\sqrt{2} - 1) π$

查看试题解析

四、培优

22. 棱锥的内切球半径 $R = \frac{3 V_{锥}}{S_{锥}}$ ，其中 $V_{锥}$ ， $S_{锥}$ 分别为该棱锥的体积和表面积，如图为某三棱锥的三视图，若每个视图都是直角边长为 $1$ 的等腰直角形，则该三棱锥内切球半径为（）

A、 $\frac{1}{3}$ B、 $\frac{3 - \sqrt{3}}{2}$ C、 $\frac{3 - \sqrt{3}}{6}$ D、 $\frac{1}{8}$

查看试题解析
23. 在正四棱锥 $P - A B C D$ 中， $A B = 8 ， P A = 4 \sqrt{10}$ ，若该棱锥的所有顶点都在球 $O$ 的表面上，则球 $O$ 的表面积为（）

A、 $800 π$ B、 $400 π$ C、 $200 π$ D、 $50 π$

查看试题解析
24. 已知某正三棱台的顶点都在半径为5的球面上，若该正三棱台的上、下底边长分别是 $3 \sqrt{3}$ 和 $5 \sqrt{3}$ ，则该正三棱台的高为（）

A、1 B、2 C、3 D、4

查看试题解析
25. 蹴鞠，又名蹴球，踢圆等，蹴有用脚蹴、踢、蹋的含义，鞠最早系外包皮革、内实米糠的球.因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动，类似今日的足球.2006年5月20日，蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录.已知某鞠的表面上有四个点 $P$ ， $A$ ， $B$ ， $C$ 恰好构成三棱锥 $P - A B C$ ，若 $A B ⊥ B C$ ， $B C ⊥ C P$ ，且 $B C = 1$ ， $C P = 2$ ， $A B = 3$ ， $A P = \sqrt{14}$ ，则该鞠的表面积为（）

A、 $\frac{7}{2} π$ B、 $7 π$ C、 $14 π$ D、 $28 π$

查看试题解析
26. 白酒又名烧酒､白干，是世界六大蒸馏酒之一，据《本草纲目》记载：“烧酒非古法也，自元时创始，其法用浓酒和糟入甑（蒸锅），蒸令气上，用器承滴露”，而饮用白酒则有专门的白酒杯，图1是某白酒杯，可将它近似的看成一个圆柱挖去一个圆台构成的组合体，图2是其直观图（图中数据的单位为厘米），则该组合体的体积为（）

A、 $\frac{55 π}{6} c m^{3}$ B、 $\frac{51 π}{6} c m^{3}$ C、 $\frac{47 π}{6} c m^{3}$ D、 $\frac{43 π}{6} c m^{3}$

查看试题解析
27. 在三棱锥 $P - A B C$ 中， $P A ⊥$ 平面 $A B C ， A B ⊥ B C$ ，且 $A B = 2$ .若三棱锥 $P - A B C$ 的外接球体积为 $36 π$ ，则当该三棱锥的体积最大时，其表面积为（）

A、 $6 + 6 \sqrt{3}$ B、 $8 + 6 \sqrt{3}$ C、 $8 + 8 \sqrt{5}$ D、 $6 + 8 \sqrt{5}$

查看试题解析
28. 阿基米德是伟大的古希腊数学家，他和高斯、牛顿并列为世界三大数学家，他一生最为满意的一个数学发现就是“圆柱容球”定理，即圆柱容器里放了一个球，该球顶天立地，四周碰边（即球与圆柱形容器的底面和侧面都相切），球的体积是圆柱体积的三分之二，球的表面积也是圆柱表面积的三分之二.今有一“圆柱容球”模型，其圆柱表面积为 $36 π$ ，则该模型中圆柱的体积与球的体积之和为（）

A、 $8 \sqrt{6} π$ B、 $12 \sqrt{6} π$ C、 $20 \sqrt{6} π$ D、 $48 \sqrt{6} π$

查看试题解析