浙江省温州市龙湾区2023-2024学年八年级上册数学开学试卷

试卷更新日期：2023-09-28 类型：开学考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分．请选出各题中唯一的正确选项，不选、多选、错选均不给分）

1. 数-6，5，0， $\frac{7}{2}$ 中最大的是（）

A、-6 B、5 C、0 D、 $\frac{7}{2}$

查看试题解析
2. 计算t⁶•t²的结果是（）

A、t⁴ B、t⁸ C、2t⁸ D、t¹²

查看试题解析
3. 新冠肺炎病毒颗粒呈圆形或椭圆形，其直径在大约是0.00000013米．数据0.00000013用科学记数法可以表示为（）

A、0.13×10^-⁶ B、1.3×10^-⁷ C、1.3×10^-⁸ D、13×10^-⁸

查看试题解析
4. 如图是703班学生最喜欢的一项球类运动的扇形统计703班学生最喜欢的，其中表示最喜欢排球的扇形圆心角是（）

A、36° B、72° C、216° D、288°

查看试题解析
5. 在同一平面内，将两个完全相同的三角板按如图摆放，可以画出两条互相平行的直线 $l_{1}$ 与 $l_{2}$ ．这样画的依据是（）

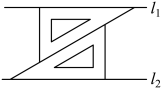A、内错角相等，两直线平行 B、同位角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，内错角相等

查看试题解析
6. 如图，生活中都把自行车的几根梁做成三角形的支架，这是利用三角形的（）

A、全等形 B、稳定性 C、灵活性 D、对称性

查看试题解析
7. 解方程 $\frac{x}{2} = 1 - \frac{x + 2}{5}$ ，以下去分母正确的是（）

A、5x＝1-2（x+2） B、5x＝10-2x+2 C、5x＝10-2x+4 D、5x＝10-2（x+2）

查看试题解析
8. 如表中给出的每一对x ， y的值都是二元一次方程ax-y＝7的解，则表中m的值为（）
x
0
1
2
3
y
-7
-4
-1
m

A、-2 B、1 C、2 D、3

查看试题解析
9. 一家工艺品厂按计件方式结算工资，小王去这家工艺品厂打工第一天得到工资60元，第二天小王比第一天多做了10件，得到工资75元，设小王第一天做了x件，可以列出方程（）

A、 $\frac{75}{x} = \frac{60}{x + 10}$ B、 $\frac{60}{x} = \frac{75}{x + 10}$ C、 $\frac{60}{x} = \frac{75}{x - 10}$ D、 $\frac{60}{x - 10} = \frac{75}{x}$

查看试题解析
10. 图1是由3个相同小长方形拼成的图形其周长为24 $c m$ ，图2中的长方形 $A B C D$ 内放置10个相同的小长方形，则长方形 $A B C D$ 的周长为（）

A、 $32 c m$ B、 $36 c m$ C、 $48 c m$ D、 $60 c m$

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

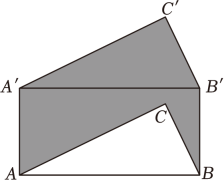
11. 因式分解：x²﹣x= ．

查看试题解析
12. 用代数式表示“ $a$ 的2倍与 $b$ 的和”.

查看试题解析
13. 把50个数据分成五组，第一、二、三、四、五组的数据个数分别是8，15，x ， 12，5．则第三组的频率为．

查看试题解析
14. 三角形三个内角度数之比是1：2：3，则此三角形是三角形．

查看试题解析
15. 如图，△ABC的边AB长为4cm ，将△ABC沿着BB′方向平移2cm得到△A'B'C''，且BB'⊥AB，则阴影部分的面积是cm² ．

查看试题解析
16. 如图1，一款暗插销由外壳AB ，开关CD ，其工作原理如图2，开关CD绕固定点O转动，此时连接点D在线段AB上，如D₁位置．开关CD绕点O顺时针旋转180°后得到C₂D₂ ，锁芯弹回至D₂E₂位置（点B与点E₂重合），此时插销闭合如图4．已知CD＝74mm ， AD₂-AC₁＝50mm ，则BE₁＝mm ．

查看试题解析

三、解答题（本题有7小题，共66分．解答需要写出必要的文字说明、演算步骤或证明过程）

17. 计算：

(1)、（-1）²- $\sqrt[3]{27}$ +|-2|；

(2)、（x+2）（x-2）-x（x+1）．

查看试题解析
18. 解下列方程（组）：

(1)、 ${\begin{cases} x = 2 y \\ 2 x + y = 5 \end{cases}$ ；

(2)、 $\frac{5 x + 3}{2} = \frac{1 + 7 x}{3}$ ．

查看试题解析
19. 先化简： $(\frac{3 x}{x - 2} - \frac{x}{x + 2}) \cdot \frac{x^{2} - 4}{x}$ ，并在-2，0，1，2中选一个合适的数求值．

查看试题解析
20. 某校为了解全校学生的上学方式，随机抽取了若干名学生进行问卷调查，问卷给出了四种上学方式供学生选择，且不能不选．将调查得到的结果绘制成如图所示的扇形统计图和条形统计图．
根据以上信息，解答下列问题：

(1)、在这次调查中，一共抽取了多少名学生？请补全条形统计图；

(2)、如果全校有1200名学生，请根据调查估计学校准备的100个自行车停车位是否够用？

查看试题解析
21. 如图，点D ， E分别在△ABC的边AB ，点F在线段CD上，且∠3＝∠B

(1)、求证：DE∥BC；

(2)、若DE平分∠ADC ， ∠2＝4∠B ，求∠1．

查看试题解析
22. 已知实数x ， y满足：x+y＝7，xy＝12．

(1)、求x²+y²的值；

(2)、将长方形ABCD和长方形CEFG按照如图方式放置，其中B ， C ， G三点在同一条直线上，连接BD ， BF ， AB＝nx ， FG＝y ，阴影部分的面积为14，求n的值．

查看试题解析
23. 如图，已知AD∥BC ， ∠A＝∠C＝m°．

(1)、如图①，求证：AB∥CD；

(2)、如图②，连结BD，若点E在AB上，且满足∠FDB＝∠BDC，并且DE平分∠ADF，求∠EBD的度数（用含m的代数式表示）.

(3)、如图③，在（2）的条件下，将线段BC沿着射线AB的方向向右平移，求∠ABD的度数．（用含m的代数式表示）

查看试题解析