湖南省长沙市重点中学2023-2024学年高二上学期数学入学考试试题

试卷更新日期：2023-09-28 类型：开学考试

进入出卷网下载

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 已知集合 $A = {x | x^{2} - x - 2 > 0}$ ， $B = {x | y = l n (3 - x)}$ ，则 $A ∩ B =$ （）

A、 ${x | 2 < x < 3}$ B、 ${x | x < 3}$ C、 ${x | x < - 1 或 2 < x < 3}$ D、 $R$

查看试题解析
2. 复数 $\frac{5}{1 + 2 i}$ 的共轭复数是（）

A、 $1 - 2 i$ B、 $1 + 2 i$ C、 $- 1 + 2 i$ D、 $- 1 - 2 i$

查看试题解析
3. 设 $x > 0$ ， $y \in R$ ，则“ $x > | y |$ ”是“ $x > y$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 已知函数 $f (x) = {\begin{cases} - x^{2} - 2 a x - 5 ， x \leq 1 \\ \frac{a}{x} ， x > 1 \end{cases}$ 是 $R$ 上的增函数，则实数a的取值范围是（）

A、 $(- \infty ， - 1]$ B、 $[- 2 ， - 1]$ C、 $[- 2 ， 0]$ D、 $(- \infty ， 0]$

查看试题解析
5. 已知 $0 < β < α < \frac{π}{2}$ ，且 $c o s (α - β) = \frac{12}{13}$ ， $c o s 2 β = \frac{3}{5}$ ，则 $c o s (α + β) =$ （）

A、 $\frac{16}{65}$ B、 $\frac{33}{65}$ C、 $\frac{56}{65}$ D、 $\frac{63}{65}$

查看试题解析
6. 已知某圆锥的侧面展开图是一个半径为r的半圆，且该圆锥的体积为 $3 π$ ，则r=（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $2 \sqrt{3}$ D、3

查看试题解析
7. 在△ABC中， $a - b = c (c o s B - c o s A)$ ，则这个三角形一定是（）

A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰或直角三角形

查看试题解析
8. 已知 $x > 0$ ， $y > 0$ ， $x + y = 1$ ，则 $\frac{2 x^{2} + x + 1}{x y}$ 的最小值为（）

A、7 B、 $\frac{14}{3}$ C、 $\sqrt{2} + 2$ D、 $2 \sqrt{2} + 1$

查看试题解析

二、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．

9. 某保险公司为客户定制了5个险种：甲，一年期短险；乙，两全保险；丙，理财类保险；丁，定期寿险；戊，重大疾病保险．各种保险按相关约定进行参保与理赔．该保险公司对5个险种的参保客户进行抽样调查，得出如下统计图例，则以下四个选项正确的是（）

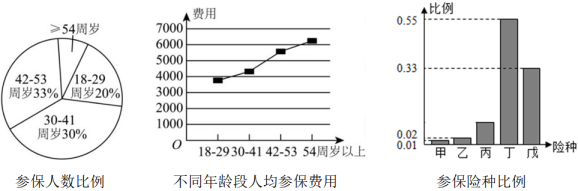A、1829周岁人群参保总费用最少 B、30周岁以上的参保人群约占参保总人群的20% C、54周岁以上的参保人数最少 D、丁险种更受参保人青睐

查看试题解析
10. 如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E，F，G分别为棱A₁D₁ ， AA₁ ， CD的中点，则（）

A、 $\vec{E F} \cdot \vec{E B} = 6$ B、B₁G⊥平面BEF C、直线AB交平面EFC于点P，则AP= $\frac{1}{3}$ AB D、点A₁到平面BEF的距离为 $\frac{2}{3}$

查看试题解析
11. 下列各式中，值为 $\frac{3}{4}$ 的是（）

A、 $s i n^{2} 30 ° + c o s^{2} 60 ° + s i n 30 ° c o s 60 °$ B、 $s i n^{2} 23 ° + c o s^{2} 53 ° + s i n 23 ° c o s 53 °$ C、 $s i n^{2} 20 ° + c o s^{2} 80 ° + \sqrt{3} s i n 20 ° c o s 80 °$ D、 $c o s^{2} 10 ° + c o s^{2} 50 ° + s i n 40 ° s i n 80 °$

查看试题解析
12. 若函数 $f (x)$ 满足：① $\forall x \in R$ ，恒有 $f (x + 2) = f (x - 2)$ ， ② $\forall x \in R$ ，恒有 $f (2 - x) = f (x)$ ， ③ $x \in [- 1 ， 1]$ 时， $f (x) = {(x + 1)}^{2} - 1$ ，则下列结论正确的是（）

A、 $f (2023) = 0$ B、 $\forall x_{1}$ ， $x_{2} \in R$ ， $| f (x_{2}) - f (x_{1}) |$ 的最大值为4 C、 $f (x)$ 的单调递增区间为 $[4 k - 1 ， 4 k + 1]$ ， $k \in Z$ D、若曲线 $y = k | x - 1 | - 1$ 与 $f (x)$ 的图象有6个不同的交点，则实数k的取值范围为（ $\frac{1}{2}$ ， 1）

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分．

13. 已知 $l o g_{2} 3 = a$ ，则 $4^{a} + 4^{- a}$ 的值为．

查看试题解析
14. 如图，在矩形ABCD中，AB=2BC=2，AC与BD的交点为M，N为边AB上任意一点（包含端点），则 $\vec{M B} \cdot \vec{D N}$ 的最大值为．

查看试题解析
15. 甲、乙两队进行篮球决赛，采取七场四胜制（当一队赢得四场胜利时该队获胜，比赛结束），根据以往比赛成绩，甲队的主客场安排依次为“主主客客主客主”，设甲队主场取胜的概率为0.8，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以4：1获胜的概率是．

查看试题解析
16. 已知△ABC的边AC= $2 \sqrt{2}$ ，且 $\frac{3}{t a n A} + \frac{2}{t a n B} = 1$ ，则△ABC的面积的最大值为．

查看试题解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17. 已知函数 $f (x) = 2 \sqrt{3} s i n x c o s x - 2 c o s^{2} x$ ．

(1)、若 $x \in R$ ，求 $f (x)$ 在 $[0 ， π]$ 的单调区间；

(2)、若 $f (x)$ 在 $[0 ， m]$ 上的最小值为 $- 2$ ，求实数m的取值范围．

查看试题解析
18. 如图，在直三棱柱ABC-A₁B₁C₁中，AB⊥BC，D是AC的中点，AA₁=AB=2．

(1)、求证：AB₁∥平面C₁BD；

(2)、若异面直线AC和A₁B₁所成角的余弦值为 $\frac{\sqrt{5}}{5}$ ，求四棱锥B-AA₁C₁D的体积．

查看试题解析
19. 某校举行了一次高一年级数学竞赛，笔试成绩在50分以上（包括50分，满分100分）共有100人，分成[50，60）、[60，70）、[70，80）、[80，90）、[90，100]五组，得到如图所示频率分布直方图．

(1)、根据频率分布直方图估计这次数学竞赛成绩的平均数和中位数（中位数精确到0.1）；

(2)、为进一步了解学困生的学习情况，从数学成绩低于70分的学生中，通过分层随机抽样的方法抽取6人，再从这6人中任取3人，求此3人分数都在[60，70）的概率．

查看试题解析
20. 记△ABC的内角A，B，C的对边分别为a ， b ， c ，分别以a ， b ， c为边长的三个正三角形的面积依次为S₁ ， S₂ ， S₃ ，已知 $S_{1} + S_{2} - S_{3} = \frac{\sqrt{3}}{2}$ ， $s i n C = \frac{2 \sqrt{5}}{5}$ ．

(1)、求△ABC的面积；

(2)、若 $s i n A s i n B = \frac{\sqrt{5}}{3}$ ，求c ．

查看试题解析
21. 如图，在四棱锥Q-ABCD中，底面ABCD是正方形，侧面QAD是正三角形，侧面QAD⊥底面ABCD，M是QD的中点．

(1)、求证：AM⊥平面QCD；

(2)、在棱BQ上是否存在点N使平面ACN⊥平面ACM成立？如果存在，求出 $\frac{B N}{N Q}$ ；如果不存在，说明理由．

查看试题解析
22. 已知函数 $f (x) = \frac{l n x}{a} + b$ （ $a \in R$ ）的图象经过点（1，0）和点（e ， 1）， $g (x) = x^{2} - 2 x$ ．

(1)、求函数 $f (x)$ 的解析式；

(2)、设 $m > 0$ ，若对于任意 $x \in [\frac{1}{m} ， m]$ ，都有 $g (x) + 2 f (m - 1) < 0$ ，求m的取值范围．

查看试题解析