广东省佛山市顺德区2023-2024学年七年级上册数学第一次月考试卷
试卷更新日期:2023-09-28 类型:月考试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 有理数 , , , 中最小的一个数是( )A、 B、 C、 D、2. 的倒数是( )A、 B、 C、 D、3. 据统计我国每年浪费的粮食约35000000吨,我们要勤俭节约,反对浪费,积极的加入“光盘行动”中来.用科学记数法表示35000000是( ).A、3.5×106 B、3.5×107 C、35×106 D、35×1074. 下列图形中属于棱柱的有( )

 A、个 B、个 C、个 D、个5. 按照图中的方式用一个平面去截长方体,则截面形状是( )
A、个 B、个 C、个 D、个5. 按照图中的方式用一个平面去截长方体,则截面形状是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 下列说法中,正确的是( )A、有理数分为正数和负数 B、绝对值是自身的数是0 C、互为相反数的两个数的绝对值相等 D、如果两个数的绝对值相等,那么这两个数相等7. 一种面粉的质量标识为“ 千克”,则下列面粉中合格的有( )A、 千克 B、 千克 C、 千克 D、 千克8. 如图所示的平面图形绕直线旋转一周,可以得到的立体图形是( )
6. 下列说法中,正确的是( )A、有理数分为正数和负数 B、绝对值是自身的数是0 C、互为相反数的两个数的绝对值相等 D、如果两个数的绝对值相等,那么这两个数相等7. 一种面粉的质量标识为“ 千克”,则下列面粉中合格的有( )A、 千克 B、 千克 C、 千克 D、 千克8. 如图所示的平面图形绕直线旋转一周,可以得到的立体图形是( ) A、
A、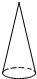 B、
B、 C、
C、 D、
D、 9. 面食不仅是中华民族饮食文化的重要组成部分,也是世界的面食之根其中,“拉面”远播世界各地,制作方法是:用一根很粗的面条,把两头捏合在一起拉伸,再捏合,反复几次,这根很粗的面条就被拉成许多细的面条,第一次捏合变根细面条,第二次捏合变根细面条,第三次捏合变根细面条,这样捏合到第次后可拉出细面条( )A、根 B、根 C、根 D、根10. 若 , 则值为( )A、或 B、或 C、或 D、或
9. 面食不仅是中华民族饮食文化的重要组成部分,也是世界的面食之根其中,“拉面”远播世界各地,制作方法是:用一根很粗的面条,把两头捏合在一起拉伸,再捏合,反复几次,这根很粗的面条就被拉成许多细的面条,第一次捏合变根细面条,第二次捏合变根细面条,第三次捏合变根细面条,这样捏合到第次后可拉出细面条( )A、根 B、根 C、根 D、根10. 若 , 则值为( )A、或 B、或 C、或 D、或二、填空题(本大题共5小题,共15.0分)
-
11. 比较大小:用“”“”或“”连接12. 某冬天中午的温度是 , 下午气温上升了 , 到夜间又下降了 , 则这天夜间的温度是13. 已知数轴上有 , 两点, , 之间的距离为 , 点与原点的距离为 , 那么点对应的数是 .14. 定义一种新运算:例如: , 则 .15. 一个立体图形,从正面看到的形状是
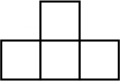 , 从左面看到的形状图是
, 从左面看到的形状图是 搭这样的立体图形,最少需要个小正方体,最多可以有个正方体.
搭这样的立体图形,最少需要个小正方体,最多可以有个正方体. 三、计算题(本大题共2小题,共16.0分)
-
16. 计算:(1)、;(2)、 .17. 计算:(1)、;(2)、 .
四、解答题(本大题共6小题,共59.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 已知一组数: , , , , .(1)、把这些数在下面的数轴上表示出来:
 (2)、请将这些数按从小到大的顺序排列用“”连接 .19. 如图是用块完全相同的小正方体搭成的几何体.
(2)、请将这些数按从小到大的顺序排列用“”连接 .19. 如图是用块完全相同的小正方体搭成的几何体.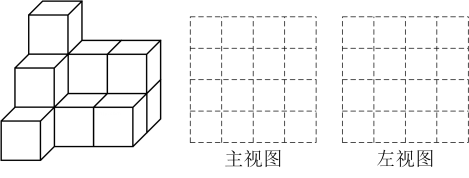 (1)、请在方格中分别画出它的主视图、左视图;(2)、如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和主视图不变,那么最多可以再添加个小正方体.20. 已知与互为相反数,与互为倒数,的绝对值等于 , 求的值.21. 李明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
(1)、请在方格中分别画出它的主视图、左视图;(2)、如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和主视图不变,那么最多可以再添加个小正方体.20. 已知与互为相反数,与互为倒数,的绝对值等于 , 求的值.21. 李明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子. (1)、共有种弥补方法;(2)、任意画出一种成功的设计图在图中补充;(3)、在你帮忙设计成功的图中,要把 , , , , , 这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加得直接在图中填上22. 某风筝加工厂计划一周生产某种型号的风筝700只,平均每天生产100只,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(增产记为正、减产记为负);
(1)、共有种弥补方法;(2)、任意画出一种成功的设计图在图中补充;(3)、在你帮忙设计成功的图中,要把 , , , , , 这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加得直接在图中填上22. 某风筝加工厂计划一周生产某种型号的风筝700只,平均每天生产100只,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(增产记为正、减产记为负);星期
一
二
三
四
五
六
日
增减
(1)、根据记录的数据,该厂生产风筝最多的一天是星期;(2)、产量最多的一天比产量最少的一天多生产多少只风筝?(3)、该厂实行每周计件工资制,每生产一只风筝可得20元,若超额完成任务,则超过部分每只另奖5元;少生产一只扣4元,那么该厂工人这一周的工资总额是多少元?23. 观察下列两个等式: , , 给出定义如下:我们称使等式成立的一对有理数 , 为“共生有理数对”,记为 , 如数对 , , 都是“共生有理数对”.
(1)、判断数对 , 是否为“共生有理数对”,并说明理由;(2)、若是“共生有理数对”,且 , 求的值;(3)、若是“共生有理数对”,则是“共生有理数对”吗?请说明理由.