广西南宁三十七中2023-2024学年八年级上册数学第一次大作业试卷
试卷更新日期:2023-09-28 类型:月考试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列现象中,属于平移的是( )A、滚动的足球 B、转动的电风扇叶片 C、正在上升的电梯 D、正在行驶的汽车后轮2. 下列各项中,两个图形属于全等图形的是( )A、
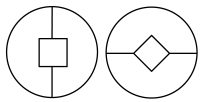 B、
B、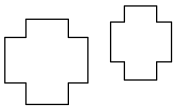 C、
C、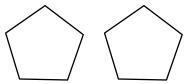 D、
D、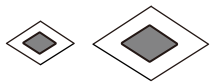 3. 画△ABC中AC边上的高,下列四个画法中正确的是( )A、
3. 画△ABC中AC边上的高,下列四个画法中正确的是( )A、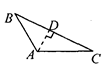 B、
B、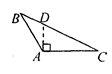 C、
C、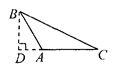 D、
D、 4. 不等式组的解集为 , 在下列数轴上表示正确的( )A、
4. 不等式组的解集为 , 在下列数轴上表示正确的( )A、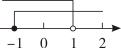 B、
B、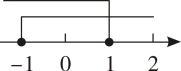 C、
C、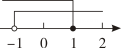 D、
D、 5. 在平面直角坐标系中,下列各点在轴上的是( )A、、 B、、 C、 D、、6. 如图,将军要从村庄A去村外的河边饮马,有三条路AB、AC、AD可走,将军沿着AB路线到的河边,他这样做的道理是( )
5. 在平面直角坐标系中,下列各点在轴上的是( )A、、 B、、 C、 D、、6. 如图,将军要从村庄A去村外的河边饮马,有三条路AB、AC、AD可走,将军沿着AB路线到的河边,他这样做的道理是( ) A、两点之间,线段最短 B、两点之间,直线最短 C、两点确定一条直线 D、直线外一点与直线上各点连接的所有线段中,垂线段最短7. 已知实数的一个平方根是 , 则它的另一个平方根是( )A、 B、 C、 D、8. 设 , 则下列式子不正确的是( )A、 B、 C、 D、9. 如图,能判定的是( )
A、两点之间,线段最短 B、两点之间,直线最短 C、两点确定一条直线 D、直线外一点与直线上各点连接的所有线段中,垂线段最短7. 已知实数的一个平方根是 , 则它的另一个平方根是( )A、 B、 C、 D、8. 设 , 则下列式子不正确的是( )A、 B、 C、 D、9. 如图,能判定的是( )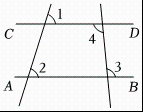 A、 B、 C、 D、10. 已知,如图,是内部的一条射线,是射线上任意点, , , 下列条件中: , , , , 能判定是的角平分线的有( )
A、 B、 C、 D、10. 已知,如图,是内部的一条射线,是射线上任意点, , , 下列条件中: , , , , 能判定是的角平分线的有( )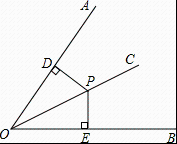 A、个 B、个 C、个 D、个11. 《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )A、 B、 C、 D、12. 如图,已知 , , , , , , ……,按这样的规律,则点的坐标为( )
A、个 B、个 C、个 D、个11. 《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )A、 B、 C、 D、12. 如图,已知 , , , , , , ……,按这样的规律,则点的坐标为( )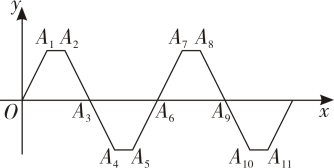 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共12.0分)
-
13. 如图所示,人字梯中间一般会设计一“拉杆”.这样做的依据是.
 14. 已知三角形的三边长分别是8、10、x,则x的取值范围是.15. 比较大小:16. 一个多边形的内角和等于它的外角和的倍,则这个多边形的边数是 .17. 如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动分钟后△CAP与△PQB全等.
14. 已知三角形的三边长分别是8、10、x,则x的取值范围是.15. 比较大小:16. 一个多边形的内角和等于它的外角和的倍,则这个多边形的边数是 .17. 如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动分钟后△CAP与△PQB全等.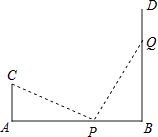 18. 三个同学对问题“若方程组的解是 , 求方程组的解”提出各自的想法.甲说:“这个题目条件不够,不能求解”;乙说:“它们的系数有一定规律,可以试试”;丙说“能不能把第二个方程组的两个方程的两边都除以 , 通过换元替代的方法来解决”参考他们的讨论,求出方程组的解是 .
18. 三个同学对问题“若方程组的解是 , 求方程组的解”提出各自的想法.甲说:“这个题目条件不够,不能求解”;乙说:“它们的系数有一定规律,可以试试”;丙说“能不能把第二个方程组的两个方程的两边都除以 , 通过换元替代的方法来解决”参考他们的讨论,求出方程组的解是 .三、计算题(本大题共1小题,共6.0分)
-
19. 计算:.
四、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
20. 解不等式组:21. 如图,已知三角形的顶点 , , 将三角形向右平移个单位长度,再向下平移个单位长度得到三角形 , 其中点 , , 分别为点 , , 的对应点.
 (1)、画出三角形 , 并直接写出点 , , 的坐标;(2)、若三角形内有一点经过以上平移后的对应点为 , 直接写出点的坐标;(3)、求三角形的面积.22. 某校八年级学生进行了一次视力调查,绘制出频数分布表和频数分布直方图的一部分如下.请根据图表信息回答下列问题:
(1)、画出三角形 , 并直接写出点 , , 的坐标;(2)、若三角形内有一点经过以上平移后的对应点为 , 直接写出点的坐标;(3)、求三角形的面积.22. 某校八年级学生进行了一次视力调查,绘制出频数分布表和频数分布直方图的一部分如下.请根据图表信息回答下列问题:视力
频数(人)
频率
4.0≤x<4.3
20
0.1
4.3≤x<4.6
40
0.2
4.6≤x<4.9
70
0.35
4.9≤x<5.2
a
0.3
5.2≤x<5.5
10
b
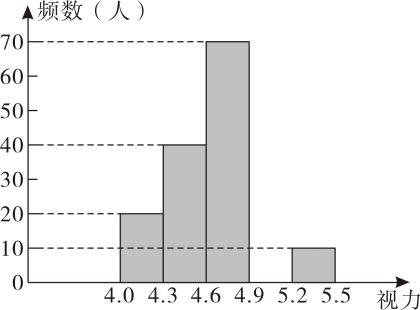
(每组数据含最小值,不含最大值)
(1)、在频数分布表中,a的值为 , b的值为.(2)、将频数分布直方图补充完整;(3)、眼科医生建议,视力低于4.6需要佩戴眼镜,该中学3000人,请估算戴眼镜的学生有多少?23. 如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.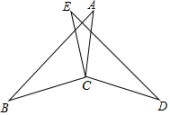 (1)、求证:BC=DC;(2)、若∠A=25°,∠D=15°,求∠ACB的度数.24. 数学课上老师提出“请对三角形内角和等于进行说理”
(1)、求证:BC=DC;(2)、若∠A=25°,∠D=15°,求∠ACB的度数.24. 数学课上老师提出“请对三角形内角和等于进行说理”已知: , , 是的三个内角.
对进行说理
小明给出如下说理过程,请补全证明过程
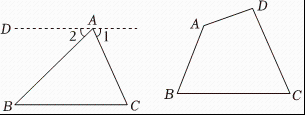
证明:过点做
▲ ▲ ( )
( )
听完小明的说理过程后,小亮提出:小明作辅助线的方法,就是借助平行线把三角形的三个内角转化成一个平角,这就启发我们可以借助平行线,对“如图,”进行说理请你帮助小亮完成作图并用文字语言叙述辅助线作法,不用写出推理过程.
25. 某旅游景点的一个商场为了抓住国庆节长假这一旅游旺季的商机,决定购进甲,乙两种纪念品,若购进甲种纪念品1件、乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.(1)、购进甲乙两种纪念品每件各需要多少元?(2)、该商场决定购进甲乙两种纪念品共100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6000元,同时甲种纪念品又不能超过60件,则该商场共有几种进货方案?(3)、若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?26. 如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CFA=α.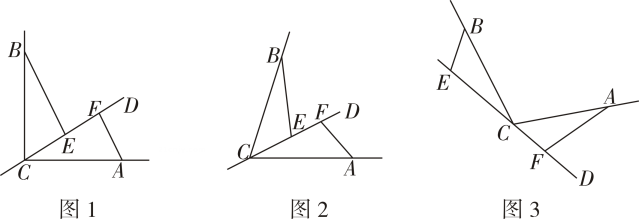 (1)、若直线CD经过∠BCA的内部,且E,F在射线CD上.
(1)、若直线CD经过∠BCA的内部,且E,F在射线CD上.①如图1,若∠BCA=90°,α=90°,证明BE=CF
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件,使①中的结论仍然成立,并说明理由.
(2)、如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF、BE,AF三条线段数量关系的合理猜想,并简述理由.
-