福建省福州市鼓楼区教育学院附中2023-2024学年八年级上册数学开学试卷

试卷更新日期：2023-09-28 类型：开学考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列四组数中，以三个数据为长的三条线段能够首尾顺次相接组成三角形的是（）

A、1，2，3 B、2，3，3 C、2，3，5 D、2，3，7

查看试题解析
2. 如图， $△ A O C$ ≌ $△ D O B$ ， $C$ ， $B$ 是对应点，下列结论错误的是（）

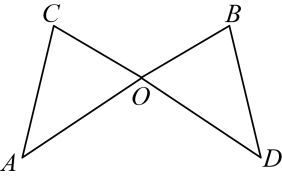A、 $∠ C$ 和 $∠ B$ 是对应角 B、 $∠ A O C$ 和 $∠ D O B$ 是对应角 C、 $O A$ 与 $O B$ 是对应边 D、 $A C$ 和 $D B$ 是对应边

查看试题解析
3. 等腰三角形的周长为26cm，一边长为6cm，那么腰长为（　　）

A、6cm B、10cm C、6cm或10cm D、14cm

查看试题解析
4. 五边形的内角和是（）

A、180° B、360° C、540° D、720°

查看试题解析
5. 如图，将一副直角三角板按如图所示叠放，其中 $∠ C = 90 °$ ， $∠ B = 45 °$ ， $∠ E = 30 °$ ，则 $∠ B F D$ 的大小是（）

A、 $10 °$ B、 $15 °$ C、 $25 °$ D、 $30 °$

查看试题解析
6. 下列正多边形瓷砖中，若仅用种瓷砖铺地面，则不能将地面密铺的是（）

A、正三角形 B、正四边形 C、正五边形 D、正六边形

查看试题解析
7. 正n边形的一个外角等于30°，则n的值为（）

A、12 B、16 C、8 D、15

查看试题解析
8. 在 $△ A B C$ 和 $△ D E F$ 中， $A B = D E$ ， $∠ A = ∠ D$ ，若要证明 $△ A B C$ ≌ $△ D E F$ ，还需要补充一个条件，则正确的补充方法是（）

A、 $B C = D F$ B、 $A C = E F$ C、 $B C = E F$ D、 $A C = D F$

查看试题解析
9. 如图，在△ABC中，AB＝AC ， ∠A＝36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有（　　）

A、5个 B、4个 C、3个 D、2个

查看试题解析
10. 如图，在四边形 $A B C D$ 中， $∠ A + ∠ D = α$ ， $∠ A B C$ 的平分线与 $∠ B C D$ 的平分线交于点 $P$ ，则 $∠ P =$ （）

A、 $90 ° - \frac{1}{2} α$ B、 $90 ° + \frac{1}{2} α$ C、 $\frac{1}{2} α$ D、 $360 ° - α$

查看试题解析

二、填空题（本大题共7小题，共21.0分）

11. 如图，已知△ABC≌△ADE，若AB＝7，AC＝3，则BE的值为

查看试题解析
12. 某科技小组制作了一个机器人，它能根据指令要求进行行走和旋转．某一指令规定：机器人先向前行走 $1$ 米，然后左转 $45 °$ ，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了米．

查看试题解析
13. 如图，在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点 $D$ ， $A E ⊥ B C$ 于点 $E$ ， $∠ B = 40 °$ ， $∠ C = 60 °$ ，则 $∠ D A E =$ $° .$

查看试题解析
14. 如图，将一张长方形纸片沿 $E F$ 折叠后，点 $D$ 、 $C$ 分别落在点 $D'$ 、 $C'$ 的位置， $E D'$ 的延长线与 $B C$ 相交于点 $G$ ，若 $∠ E F G = 58 °$ ，则 $∠ 1 =$ $° .$

查看试题解析
15. 已知 $△ A B C$ 的三边长分别是 $a$ 、 $b$ 、 $c$ ，化简 $| a + b - c | - | b - a - c | =$ ．

查看试题解析
16. 如图， $△ A D F$ 中，点 $B$ ， $C$ 分别在 $A D$ ， $A F$ 上， $D C$ 与 $B F$ 交于点 $E$ ，若 $D E$ ： $C E = 2$ ： $1$ ， $S_{△ D E F} = 6$ ， $S_{△ D B E} = 4$ ，则 $△ A B C$ 的面积 $=$ ．

查看试题解析
17. 如图， $D$ 是 $△ A B C$ 的 $B C$ 边上的一点， $∠ B = ∠ B A D$ ， $∠ A D C = 80 °$ ， $∠ B A C = 70 °$ ．

(1)、求 $∠ B$ 的度数．

(2)、求 $∠ C$ 的度数．

查看试题解析

三、解答题（本大题共5小题，共40.0分。解答应写出文字说明，证明过程或演算步骤）

18. 一个多边形的内角和是它的外角和的3倍，求这个多边形的边数。

查看试题解析
19. 如图， $△ A D E$ ≌ $△ B C F$ ， $A D = 8 c m$ ， $C D = 6 c m$ ，试求 $B D$ 的长．

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ A B C = 3 ∠ C$ ， $A D$ 平分 $∠ B A C$ ， $B E ⊥ A D$ 于 $E$ ，若 $∠ B A C = 60 °$ ，求 $∠ A D B$ 的度数．

查看试题解析
21. 我们学过三角形的相关知识，在“信息技术应用”——画图找规律的实践学习中，我们发现了几个基本事实：三角形的三条中线交于一点，三角形的三条角平分线交于一点，三角形的三条高所在的直线交于一点.请根据以上的基本事实，解决下面的问题.
如图，钝角三角形 $A B C$ 中， $A D$ ， $B E$ 分别为 $B C$ ， $C A$ 边上的高.

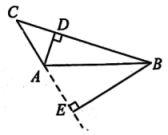(1)、请用无刻度直尺画出 $A B$ 边上的高 $C F$ （保留作图痕迹，不写作法）；

(2)、在（1）的条件下，若 $A B = 4$ ， $A C = 2$ ，求高 $C F$ 与 $B E$ 的比是多少？

查看试题解析
22. 阅读下列材料并解答问题：在一个三角形中，如果一个内角的度数是另一个内角度数的3倍，那么这样的三角形我们称为“梦想三角形”例如：一个三角形三个内角的度数分别是120°，40°，20°，这个三角形就是一个“梦想三角形”.反之，若一个三角形是“梦想三角形”，那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.

(1)、如果一个“梦想三角形”有一个角为108°，那么这个“梦想三角形”的最小内角的度数为

(2)、如图1，已知∠MON＝60°，在射线OM上取一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C（点C不与O、B重合），若∠ACB=80°.判定△AOB、△AOC是否是“梦想三角形”，为什么？

(3)、如图2，点D在△ABC的边上，连接DC，作∠ADC的平分线交AC于点E，在DC上取一点F，使得∠EFC+∠BDC＝180°，∠DEF＝∠B.若△BCD是“梦想三角形”，求∠B的度数.

查看试题解析