福建省福州市仓山区2022-2023学年七年级下学期数学期末试题

试卷更新日期：2023-09-28 类型：期末考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

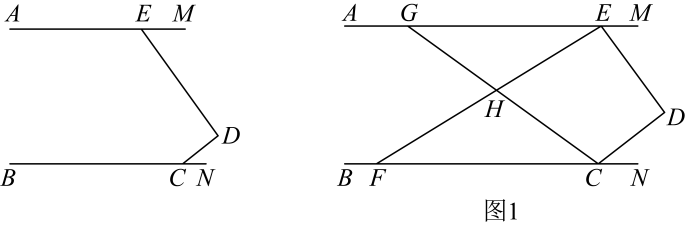
A、 $\pm 3$ B、3 C、 $\pm 81$ D、81

查看试题解析
2. 下列调查中，适合全面调查的是（）

A、调查全班同学1周内在家做家务时间 B、调查某品牌袋装食品是否含有防腐剂 C、调查闽江流域现有鱼的种类 D、调查夏季冷饮市场上奶茶的质量

查看试题解析
3. 如图，将一副三角板顶点 $O$ 靠在一直尺的边上，若 $∠ A O C = 50 °$ ，则 $∠ B O D$ 的度数（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
4. 已知二元一次方程组 ${\begin{array}{l} 2 x - 4 y = 9 ① \\ 3 x - 3 y = 12 ② \end{array}$ 则② $-$ ①得（）

A、 $x - y = 3$ B、 $x + y = 3$ C、 $5 x - 7 y = 21$ D、 $5 x + 7 y = 3$

查看试题解析
5. 某市2022年9月普通高中招生4.3万人，初中招生8.8万人，则全市中学共招生（）

A、 $13.1 \times 1 0^{2}$ 人 B、 $13.1 \times 1 0^{3}$ 人 C、 $1.31 \times 1 0^{4}$ 人 D、 $1.31 \times 1 0^{5}$ 人

查看试题解析
6. 如图，直线 $a ， b$ 被 $c$ 所截， $∠ 1 = 5 8^{∘} ， ∠ 3 = 12 2^{∘}$ ，求证： $a ∥ b$ ．

下列是佳宁同学的证明过程：

证明： $∵ ∠ 1 + ∠ 2 = 18 0^{∘} ， ∠ 1 = 5 8^{∘}$

      $∴ ∠ 2 = 18 0^{∘} - 5 8^{∘} = 12 2^{∘}$

      $∵ ∠ 3 = 12 2^{∘}$

      $∴ ∠ 2 = ∠ 3$

      $∴ a ∥ b$ （填依据）．

则下列关于上述证明过程中括号内填依据正确的是（）

A、两直线平行，同位角相等 B、两直线平行，内错角相等 C、同位角相等，两直线平行 D、内错角相等，两直线平行

查看试题解析
7. 已知一个钝角为 $(5 x + 35) °$ ，则 $x$ 的取值范围是（）

A、 $11 < x < 28$ B、 $11 < x \leq 28$ C、 $11 < x < 29$ D、 $11 < x \leq 29$

查看试题解析
8. 某校利用课后服务开展了主题为“浸润书香，放飞悦读”的读书活动．现需购买甲，乙两种图书共300本供学生阅读，其中甲种图书的单价为 $a$ 元/本，乙种图书的单价为 $2 a$ 元/本，若购买甲种图书 $x$ 本，则该校购买甲乙两种图书总费用为（）

A、 $(300 a + a x)$ 元 B、 $(300 a - a x)$ 元 C、 $(600 a + a x)$ 元 D、 $(600 a - a x)$ 元

查看试题解析
9. 已知 $a ， b$ 均属于同一类数， $a + b$ 不一定属于该类数，则这类数可以是（）

A、正有理数 B、负实数 C、整数 D、无理数

查看试题解析
10. 在平面直角坐标系 $x O y$ 中， $A (5 \sqrt{3} ， 0)$ ， $A B = 7 \sqrt{3}$ ，以点 $A$ 为圆心， $A B$ 长为半径画弧交 $x$ 轴负半轴于点 $C$ ，则点 $C$ 的坐标为（）

A、 $(- 12 \sqrt{3} ， 0)$ B、 $(- 2 \sqrt{3} ， 0)$ C、 $(0 ， - 12 \sqrt{3})$ D、 $(0 ， - 2 \sqrt{3})$

查看试题解析

二、填空题

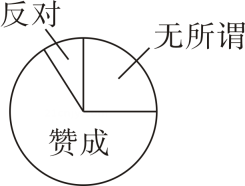
11. 8的立方根为.

查看试题解析
12. 在平面直角坐标系中 $x O y$ 中，线段 $A B$ 平移至 $A_{1} B_{1}$ 位置．若 $A (- 5 ， 8)$ 的对应点是 $A_{1} (9 ， 6)$ ，则 $B (- 8 ， 6)$ 的对应点 $B_{1}$ 的坐标是．

查看试题解析
13. 在等式 $y = k x + b$ 中，当 $x = 6$ 时， $y = 3$ ，则 $12 k + 2 b - 5$ 的值为．

查看试题解析
14. 为了鼓励学生开展课外阅读，学校公布了“阅读奖励”方案，征求了本校所有学生意见，“赞成”、“反对”、“无所谓”三种意见人数比为 $8 ： 1 ： 3$ ，并画出如图所示的扇形统计图，则图中“赞成”对应扇形的圆心角度数为．

查看试题解析
15. 若 $3^{4} = 3^{a}$ ， $3^{4} + 3^{4} + 3^{4} = 3^{b}$ ，则 $a + b =$ ．

查看试题解析
16. 已知关于 $x$ 的不等式组 ${\begin{array}{l} x \leq 3 \\ x > a \end{array}$ ，现有以下结论：
①若 $a = - 3$ ，则 $x = 2$ 是该不等式组的一个解；

②若该不等式组无解，则 $a > 3$ ；

③若该不等式组只有三个整数解，则 $0 < a < 1$ ；

④若原不等式组的解集为 $- 5 < x \leq 3$ 时，则 $a = - 5$ ．

其中正确的是（写出所有正确结论的序号）．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt[3]{- 64} + \sqrt{25}$ ；

(2)、 $2 \times (3 + \sqrt{5}) + 4 - 2 \sqrt{5}$ ．

查看试题解析
18. 解方程或方程组：

(1)、 $\frac{3 x}{2} - 16 = \frac{x}{5} - 3$ ；

(2)、 ${\begin{array}{l} x + 2 y = 5 ① \\ 5 x - 4 y = - 3 ② \end{array}$ ．

查看试题解析
19. 解不等式组 ${\begin{array}{l} 3 x + 2 \leq x + 6 ① \\ 5 x - 4 > - 3 x + 20 ② \end{array}$ ，并利用数轴确定不等式组的解集．

查看试题解析
20. 已知 $a ， b ， c$ 都是实数，若 $a = c - 3 ， b > c$ ．求证： $b > \frac{a + 2 b}{3} + 1$ ．

查看试题解析
21. 如图， $△ A B C$ ．【友情提示：尺规作图要用圆规，并保留痕迹；画完图要写完整结论】

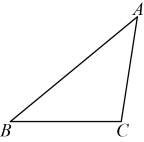(1)、尺规作图：在 $A B$ 上取一点 $D$ ，使 $B D = B C$ ；

(2)、画图：过点 $D$ 画直线 $D E ∥ B C$ 交 $A C$ 于点 $E$ ；

(3)、在（1）（2）的条件下，连接 $C D$ ，若 $∠ B C D = ∠ B D C = 70 °$ ，求 $∠ A D E$ 的度数．

查看试题解析
22. 某超市现售卖糖丸和帅童两种西瓜．已知购买2千克糖丸西瓜和1千克帅童西瓜需要花费33元，购买1千克糖丸西瓜和4千克帅童西瓜需要花费48元．

(1)、求糖丸西瓜和帅童西瓜每千克的价格分别是多少？

(2)、某工作队计划用不超过270元购买糖丸和帅童两种西瓜共25千克，求最多可购买多少千克糖丸西瓜？

查看试题解析

23. 某学校食堂计划推行午餐套餐制，现随机抽取中午在学校食堂用餐的20名学生，收集到他们午餐消费金额

x

（单位：元）的数据如下：

9 ， 13 ， 14 ， 14 ， 14 ， 11 ， 14 ， 11 ， 13 ， 13 ， 12 ， 13 ， 13 ， 11 ， 12 ， 15 ， 15 ， 12 ， 13 ， 10

．对以上数据进行整理、描述和分析．下面给出部分信息：

①这20名学生午餐消费金额数据的频数分布统计表：

消费金额	$9 \leq x < 11$	$11 \leq x < 13$	$13 \leq x < 15$	$15 \leq x < 17$
频数	2	$a$	$b$	2

②根据①中整理的四组数据绘制成一个不完整的频数分布直方图（如图）．

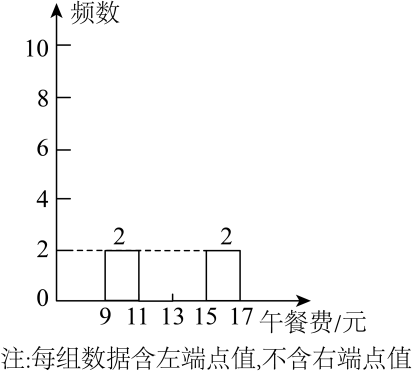
根据以上信息，回答下列问题：

(1)、直接写出频数分布统计表中

a

与

b

的值；

(2)、补全频数分布直方图；

(3)、为了合理膳食结构，学校食堂推出A ， B两种价格不同的套餐．据调查，午餐消费金额在

11 \leq x < 13

的学生中有

50 %

选择

A

套餐，消费金额在

13 \leq x < 15

的学生中有

80 %

选择

A

套餐，其余学生选择

B

套餐．若每天中午约有600名的学生在食堂用餐，估计食堂每天中午需准备

B

套餐份数．

查看试题解析

24. 如图，点 $E ， C$ 分别在射线 $A M ， B N$ 上， $∠ M E D + ∠ N C D = ∠ E D C$ ．

(1)、求证： $A M ∥ B N$ ；

(2)、如图1，点G、F在AE、BC上，连接EF、GC，且EF、GC相交于点H，∠AED=n∠AEF，∠BCD=n∠BCG，当∠DEH+∠DCH=2∠EHC时，求n的值．

(3)、在（2）条件下，若 $∠ A E F + ∠ B C G = 9 0^{∘}$ ，求证： $D E ⊥ D C$ ．

查看试题解析
25. 在平面直角坐标系 $x O y$ 中， $A (- 3 ， 0)$ ， $B (0 ， 4)$ ， $P (m ， n)$ ，且 $m$ ， $n$ 满足 ${\begin{array}{l} m + n = 2 a - 4 ① \\ m - n = 2 a + 2 ② \end{array}$ ．

(1)、求点 $P$ 的坐标；（用含 $a$ 的式子表示）

(2)、过点 $P$ 作 $P Q ∥ A B$ 交 $x$ 轴于点 $C$ ，当 $a = \frac{1}{2}$ 时，
①求 $△ P B C$ 的面积；

②若点 $D$ 在直线 $P Q$ 上，且点 $D$ 的横坐标为5，求点 $D$ 的纵坐标．

查看试题解析