福建省福州市闽清县2022-2023学年八年级下学期数学6月期末试题
试卷更新日期:2023-09-28 类型:月考试卷
一、单选题
-
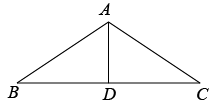
1. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≥3 B、x≤3 C、x>3 D、x<32. 已知关于x的方程的一个根为 , 则实数m的值为( )A、4 B、 C、3 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 点在正比例函数()的图象上,则k的值为( )A、-15 B、15 C、 D、5. 如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
 A、5 B、6 C、8 D、106. 下列命题是真命题的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是矩形 C、对角线互相垂直的矩形是正方形 D、四边相等的平行四边形是正方形7. A,B两名射击运动员进行了相同次数的射击,下列关于他们射击成绩的平均数和方差的描述中,能说明A成绩较好且更稳定的是( )A、且. B、且. C、且 D、且.8. 用配方法解方程 ,配方后所得的方程是( )A、 B、 C、 D、9. 某厂家今年一月份的口罩产量是30万个,三月份的口罩产量是50万个,若设该厂家一月份到三月份的口罩产量的月平均增长率为x.则所列方程为( )A、30(1+x)2=50 B、30(1﹣x)2=50 C、30(1+x2)=50 D、30(1﹣x2)=5010. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )
A、5 B、6 C、8 D、106. 下列命题是真命题的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是矩形 C、对角线互相垂直的矩形是正方形 D、四边相等的平行四边形是正方形7. A,B两名射击运动员进行了相同次数的射击,下列关于他们射击成绩的平均数和方差的描述中,能说明A成绩较好且更稳定的是( )A、且. B、且. C、且 D、且.8. 用配方法解方程 ,配方后所得的方程是( )A、 B、 C、 D、9. 某厂家今年一月份的口罩产量是30万个,三月份的口罩产量是50万个,若设该厂家一月份到三月份的口罩产量的月平均增长率为x.则所列方程为( )A、30(1+x)2=50 B、30(1﹣x)2=50 C、30(1+x2)=50 D、30(1﹣x2)=5010. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )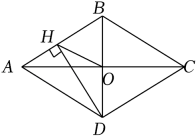 A、4 B、4 C、8 D、8
A、4 B、4 C、8 D、8二、填空题
-
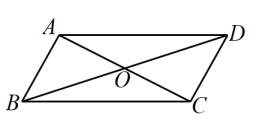
11. 请写出一个y随x增大而增大的一次函数表达式 .12. 小丽的笔试成绩为100分,面试成绩为90分,若笔试成绩、面试成绩按6:4计算平均成绩,则小丽的平均成绩是分.13. 将直线 向下平移2个单位长度,平移后直线的解析式为.14. 如图,在中,AD=10,对角线AC与BD相交于点O , AC+BD=22,则△BOC的周长为
 15. 实数 , 是一元二次方程的两个根,则多项式值为 .16. 甲、乙两人沿同一条直路走步,如果两人分别从这条道路上的两处同时出发,都以不变的速度相向而行,图1是甲离开处后行走的路程(单位:)与行走时(单位:)的函数图象,图2是甲、乙两人之间的距离(单位:)与甲行走时间x(单位:)的函数图象,则 .
15. 实数 , 是一元二次方程的两个根,则多项式值为 .16. 甲、乙两人沿同一条直路走步,如果两人分别从这条道路上的两处同时出发,都以不变的速度相向而行,图1是甲离开处后行走的路程(单位:)与行走时(单位:)的函数图象,图2是甲、乙两人之间的距离(单位:)与甲行走时间x(单位:)的函数图象,则 .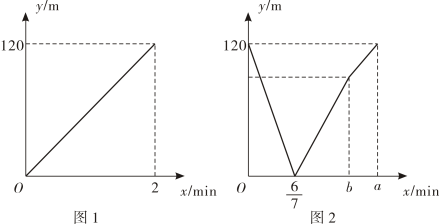
三、解答题
-
17. 计算: .18. 解方程19. 如图,在中,点E,点F分别是和的中点.求证: .
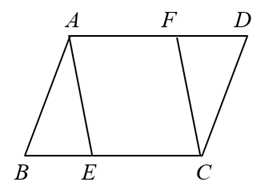 20. 已知关于x的一元二次方程有两个不等实数根 , .(1)、求k的取值范围;(2)、若 , 求k的值.21. 为了加强对青少年防溺水安全教育,5月底某校开展了“远离溺水,珍爱生命”的防溺水安全知识比赛.下面是从参赛学生中随机收集到的20名学生的成绩(单位:分):
20. 已知关于x的一元二次方程有两个不等实数根 , .(1)、求k的取值范围;(2)、若 , 求k的值.21. 为了加强对青少年防溺水安全教育,5月底某校开展了“远离溺水,珍爱生命”的防溺水安全知识比赛.下面是从参赛学生中随机收集到的20名学生的成绩(单位:分):87/99/86/89/91/91/95/96/87/97
91/97/96/86/96/89/100/91/99/97
整理数据:
成绩(分)
86
87
89
91
95
96
97
99
100
学生人数(人)
2
2
2
a
1
3
_b__
2
1
分析数据:
平均数
众数
中位数
93
c
d
解决问题:
(1)、直接写出上面表格中的a , b , c , d的值;(2)、若成绩达到95分及以上为“优秀”等级,求“优秀”等级所占的百分率;(3)、请估计该校1500名学生中成绩达到95分及以上的学生人数.22. 如图,四边形中, , , 点D .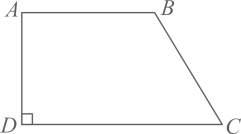 (1)、用尺规作的角平分线,交点E;(不写作法,保留作图痕迹)(2)、连接 . 求证:四边形菱形.23. 某水果店购进甲、乙两种苹果的进价分别为8元、12元 , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.
(1)、用尺规作的角平分线,交点E;(不写作法,保留作图痕迹)(2)、连接 . 求证:四边形菱形.23. 某水果店购进甲、乙两种苹果的进价分别为8元、12元 , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.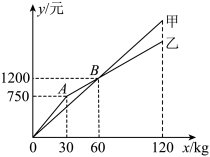 (1)、当甲、乙两种苹果销售量都为60时,甲种苹果销售额元,乙种苹果销售额元;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元,求a的值.
(1)、当甲、乙两种苹果销售量都为60时,甲种苹果销售额元,乙种苹果销售额元;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元,求a的值.