福建省福州市闽侯县2022-2023学年七年级下学期数学期末试题

试卷更新日期：2023-09-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列调查中，调查方式选择合理的是（）

A、为了了解某一品牌家具的甲醛含量，选择全面调查； B、为了了解神舟飞船的设备零件的质量情况，选择抽样调查； C、为了了解某公园全年的游客流量，选择抽样调查； D、为了了解一批袋装食品是否含有防腐剂，选择全面调查.

查看试题解析
2. 如图，在数轴上表示的x的取值范围是（）

A、 $x < 2$ B、 $x \leq 2$ C、 $x > 2$ D、 $x \geq 2$

查看试题解析
3. 下列四个图形中， $∠ 1$ 与 $∠ 2$ 是邻补角的是（）

A、 B、 C、 D、

查看试题解析
4. 已知 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 是二元一次方程 $a x + 3 y = 0$ 的解，则 $a$ 的值为（）

A、0 B、1 C、2 D、3

查看试题解析
5. 课间操时，小华、小军、小刚的位置如图．小华对小刚说：“如果我的位置用 $(0 ， 0)$ 表示，小军的位置用 $(2 ， 1)$ 表示，那么你的位置可以表示成（）

A、 $(5 ， 4)$ B、 $(4 ， 5)$ C、 $(3 ， 4)$ D、 $(4 ， 3)$

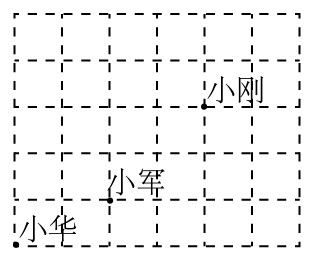查看试题解析
6. 下列命题中，真命题的是（）

A、相等的角是对顶角 B、两条直线被第三条直线所截，内错角相等 C、垂直于同一条直线的两条直线互相垂直 D、平行于同一条直线的两条直线互相平行

查看试题解析
7. 在平面直角坐标系中 $A (- 3 ， - 2)$ ， $B (3 ， 4)$ ， $C (x ， y)$ ，若 $A C ∥ x$ 轴，则线段 $B C$ 取最小值时点 $C$ 的坐标为（）

A、 $(3 ， - 4)$ B、 $(3 ， - 2)$ C、 $(- 3 ， 4)$ D、 $(- 3 ， 2)$

查看试题解析
8. 《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有醇酒一斗，值钱五十；行酒一斗，值钱一十．今将钱三十，得酒二斗．问醇酒、行酒各得几何？”其意思是：今有醇酒（优质酒）1斗，价值50钱；行酒（劣质酒）1斗，价值10钱；现有30钱，买得2斗酒．问可以买醇酒和行酒各多少斗？设可以买醇酒x斗，行酒y斗，则可列方程组为（）

A、 ${\begin{array}{l} 10 x + 50 y = 30 \\ x + y = 2 \end{array}$ B、 ${\begin{array}{l} 50 x + 10 y = 30 \\ x + y = 2 \end{array}$ C、 ${\begin{array}{l} 10 x + 50 y = 2 \\ x + y = 30 \end{array}$ D、 ${\begin{array}{l} 50 x + 10 y = 2 \\ x + y = 30 \end{array}$

查看试题解析
9. 已知 $a$ 是正数，下列关于 $x$ 的不等式组无解的是（）

A、 ${\begin{array}{l} x > a \\ x > 0 \end{array}$ B、 ${\begin{array}{l} x > a \\ x < 0 \end{array}$ C、 ${\begin{array}{l} x < a \\ x > 0 \end{array}$ D、 ${\begin{array}{l} x < a \\ x < 0 \end{array}$

查看试题解析
10. 在平面直角坐标系中，将 $A (1 ， m^{2})$ ，沿着 $y$ 轴的负方向向下平移 $2 m^{2} + 3$ 个单位后得到 $B$ 点．有四个点 $M (1 ， - m^{2} - 4)$ ， $N (1 ， - 2 m^{2} - 3)$ ， $P (1 ， - m^{2})$ ， $Q (1 ， - 3 m^{2})$ 一定在线段 $A B$ 上的是（）

A、点 $M$ B、点 $N$ C、点 $P$ D、点 $O$

查看试题解析

二、填空题

11. 请写出一个比﹣ $\sqrt{2}$ 小的无理数：.

查看试题解析
12. 点 $A (3 ， a + 1)$ 在 $x$ 轴上，点 $B (b - 2 ， 5)$ 在 $y$ 轴上，则 $a^{b}$ 的值为．

查看试题解析
13. 体育老师从七年级学生中抽取40名参加全校的健身操比赛．这些学生身高（单位； $c m$ ）的最大值为186，最小值为158．若取组距为3，则可以分成组．

查看试题解析
14. 如图， $A B ∥ C D$ ， $∠ D = 36 °$ ， $∠ A B C = 65 °$ ，则 $∠ C B D$ 的度数是．

查看试题解析
15. 如果 $| x - 3 | = x - 3$ ，那么 $x$ 的取值范围是．

查看试题解析
16. 定义：若两个有理数的和等于这两个有理数的积，则称这两个数是一对“友好数”．如：有理数 $\frac{4}{3}$ 与4，因为 $\frac{4}{3} + 4 = \frac{4}{3} \times 4$ ，所以 $\frac{4}{3}$ 与4是一对“友好数”．设 $x$ （ $x \neq 0$ 或 $x_{1} \neq 1$ ）的“友好数”为 $x_{1}$ ； $x_{1}$ 的倒数为 $x_{2}$ ； $x_{2}$ 的“友好数”为 $x_{3}$ ； $x_{3}$ 的倒数为 $x_{4}$ ；……依次按如上的操作，得到一组数： $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ ， …， $x_{n}$ ．当 $x = \frac{3}{2}$ 时， $x_{2023}$ 的值为．

查看试题解析

三、解答题

17. 计算下列各式的值：

(1)、 $3 \sqrt{2} - | \sqrt{3} - \sqrt{2} |$ ；

(2)、 $\sqrt{3} (\sqrt{3} + \frac{1}{\sqrt{3}})$ ．

查看试题解析
18. 解方程组： ${\begin{array}{l} \frac{1}{2} x + 3 y = - 6 \\ \frac{1}{2} x + y = 2 \end{array}$ ．

查看试题解析
19. 解不等式组： ${\begin{array}{l} 5 x - 1 > 3 (x + 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$

查看试题解析
20. 如图，已知 $∠ B A F = ∠ A F D$ ， $∠ A B C + ∠ C D E = 180 °$ ．求证： $B C ∥ D E$ ．

查看试题解析
21. 如图，在平面直角坐标系 $x O y$ 中， $A (5 ， 3)$ ， $B (3 ， 1)$ ， $C (1 ， 2)$ ．将三角形 $A B C$ 向左平移5个单位长度，再向上平移3个单位长度，可以得到三角形 $A_{1} B_{1} C_{1}$ ，其中点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 分别与点 $A$ ， $B$ ， $C$ 对应．

(1)、画出平移后的三角形 $A_{1} B_{1} C_{1}$ ；

(2)、直接写出 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 三个点的坐标；

(3)、若点 $P$ 在 $y$ 轴上，以 $A_{1}$ ， $B_{1}$ ， $P$ 为顶点的三角形面积为2，求点 $P$ 的坐标．

查看试题解析
22. 为了更加扎实、有效地开展劳动教育，落实“五育并举”，某校倡议学生在家帮助父母做一些力所能及的家务．校学生会随机抽取该校部分学生进行问卷调查．现得到如下信息：
根据以上信息，回答下列问题：

(1)、这次抽样调查的学生人数是， $C$ 对应的扇形圆心角的度数是°；

(2)、请根据题中已有的信息补全频数分布直方图；

(3)、该校有1800名学生，根据抽样调查结果，请你估计该校平均每周做家务的时间不少于3小时的学生人数．

查看试题解析
23. 学校为了支持体育社团开展活动，鼓励同学们加强锻炼，准备增购一些羽毛球和乒乓球拍．

(1)、根据图中信息，求出每支羽毛球拍和每支乒乓球拍的价格；

(2)、学校准备用不超过6400元购羽毛球拍和乒乓球拍，且乒乓球拍的数量为羽毛球拍数量的3倍，请问最多能购买多少支羽毛球拍？

查看试题解析
24. 若点 $P (x ， y)$ 的坐标满足 ${\begin{array}{l} x + y = 2 a - b - 5 \\ x - y = b - 5 \end{array}$ ．

(1)、若点 $P$ 的坐标为 $(- 2 ， - 1)$ ，求 $a$ ， $b$ 的值；

(2)、若点 $P$ 在第二象限，且符合要求的整数 $a$ 只有五个，求 $b$ 的取值范围；

(3)、若点 $P$ 为不在 $x$ 轴上的点，且关于 $z$ 的不等式 $y z + 3 x + 15 > 0$ 的解集为 $z < \frac{3}{5}$ ，求关于 $t$ 的不等式 $a t \leq b$ 的解集．

查看试题解析
25. 如图1，在平面直角坐标系中，已知点 $A (- 5 ， - 1)$ ， $B (- 3 ， 2)$ ，将线段 $A B$ 平移至线段 $C D$ ，使点 $A$ 的对应点 $C$ 恰好落在 $x$ 轴的正半轴上，设点 $C$ 的坐标为 $(k ， 0)$ ，点 $B$ 的对应点 $D$ 在第一象限．

(1)、求点 $D$ 的坐标（用含 $k$ 的式子表示）；

(2)、连接 $B D$ ， $B C$ ．如图2，若三角形 $B C D$ 的面积为8，求 $k$ 的值；

(3)、连接 $A D$ ，如图3，分别作 $∠ A B C$ 和 $∠ A D C$ 的平分线，交于点 $P$ ，试探究 $∠ B A D$ ， $∠ B C D$ 和 $∠ B P D$ 之间的等量关系，并说明理由．

查看试题解析