福建省福州市台江区2022-2023学年七年级下学期数学期末试题
试卷更新日期:2023-09-28 类型:期末考试
一、单选题
-
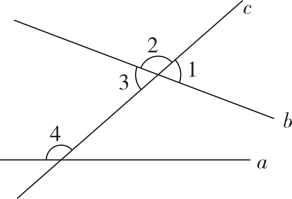
1. 下列给出的数中,是无理数的是( )A、 B、0 C、 D、2. 下列有序数对满足方程的是( )A、 B、 C、 D、3. 如图,直线 , 被直线所截,则下列符合题意的结论是( )
 A、 B、 C、 D、4. 空气是由多种气体混合组成的,为了直观地介绍空气各成分的百分比,最适合使用的统计图是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布直方图5. 下列调查中,适合采用全面调查方式的是( )A、对某班学生的校服尺寸大小的调查 B、对福州闽江的水质情况的调查 C、对我区市民“五一”出游情况的调查 D、对我国初中生近视情况的调查6. 下列变形错误的是( )A、由得 B、由得 C、由得 D、由得7. 某学校的平面示意图如图所示,如果医院所在位置的坐标为 , 则所在的位置是( )
A、 B、 C、 D、4. 空气是由多种气体混合组成的,为了直观地介绍空气各成分的百分比,最适合使用的统计图是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布直方图5. 下列调查中,适合采用全面调查方式的是( )A、对某班学生的校服尺寸大小的调查 B、对福州闽江的水质情况的调查 C、对我区市民“五一”出游情况的调查 D、对我国初中生近视情况的调查6. 下列变形错误的是( )A、由得 B、由得 C、由得 D、由得7. 某学校的平面示意图如图所示,如果医院所在位置的坐标为 , 则所在的位置是( )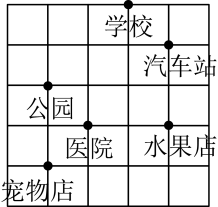 A、医院 B、学校 C、汽车站 D、水果店8. 如图,估计的值所对应的点可能落在( )
A、医院 B、学校 C、汽车站 D、水果店8. 如图,估计的值所对应的点可能落在( )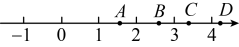 A、点A处 B、点B处 C、点C处 D、点D处9. 《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”译文:今有优质酒1斗的价格是50钱,普通酒1斗的价格是10钱,现在买了两种酒2斗,共付30钱.问优质酒、普通酒各买多少斗? 如果设买优质酒x斗,普通酒y斗,则可列方程组为( )
A、点A处 B、点B处 C、点C处 D、点D处9. 《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”译文:今有优质酒1斗的价格是50钱,普通酒1斗的价格是10钱,现在买了两种酒2斗,共付30钱.问优质酒、普通酒各买多少斗? 如果设买优质酒x斗,普通酒y斗,则可列方程组为( ) A、 B、 C、 D、10. 已知两个不相等的实数x , y满足: , , 则的值为( )A、 B、0 C、1 D、
A、 B、 C、 D、10. 已知两个不相等的实数x , y满足: , , 则的值为( )A、 B、0 C、1 D、二、填空题
-
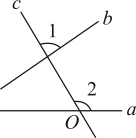
11. 把方程2x+y=1改写成用含x的式子表示y的形式,则y= .12. 已知是方程的一个解,那么a的值为 .13. 把命题“对顶角相等”改写成“如果……,那么……”的形式为 .14. 已知点M(3a-9,1-a),将M点向左平移3个单位长度后落在y轴上,则点M的坐标为 .15. 如图,直线c与a、b相交, , , 要使直线a与b平行,直线a绕点O逆时针旋转的度数最小的度数是°.
 16. 如图,在大正方形中剪去一个小正方形,再将图中的阴影剪拼成一个长方形,如图2,这个长方形的长为24,宽为16,则图2中S2部分的面积是 .
16. 如图,在大正方形中剪去一个小正方形,再将图中的阴影剪拼成一个长方形,如图2,这个长方形的长为24,宽为16,则图2中S2部分的面积是 .
三、解答题
-
17. 计算: .18. 解方程组:(1)、;(2)、19. 解不等式 , 并把解集在数轴上表示出来.20. 已知不等式与同时成立,求的整数值.21. 如图,点A在直线l外,点B在直线l上,选择适当的工具画图.
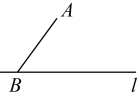 (1)、过点A , 画直线l的垂线 , 垂足为C;(2)、平移 , 点A、B、C的对应点分别是点D、C、E , 画出平移后的;(3)、如果 , 求的度数.22. 某小区为了解居民的健步走情况,调查了部分居民某天行走的步数(单位:千步),并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图.
(1)、过点A , 画直线l的垂线 , 垂足为C;(2)、平移 , 点A、B、C的对应点分别是点D、C、E , 画出平移后的;(3)、如果 , 求的度数.22. 某小区为了解居民的健步走情况,调查了部分居民某天行走的步数(单位:千步),并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图.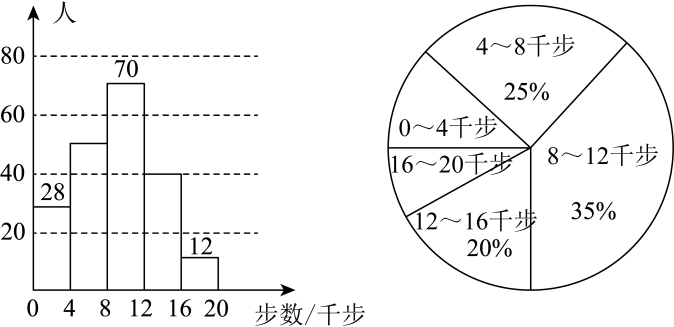
根据图表提供的信息,回答下列问题:
(1)、此次调查的样本容量是;(2)、行走步数为4~8千步的人数为人;(3)、行走步数为12~16千步的扇形圆心角为°;(4)、如该小区有3000名居民,请估算一下该小区行走步数为0~4千步的人数.23. 某校组织学生去游乐园参加拓展体验活动,活动中有“空中飞人”和“保卫地球”两个体验项目供同学选择.如果4名同学选择“空中飞人”,1名同学选择“保卫地球”,购票费用共需195元;如果3名同学选择“空中飞人”,2名同学选择“保卫地球”,购票费用共需190元.(1)、求每张“空中飞人”的票价和每张“保卫地球”的票价各为多少元;(2)、在(1)的条件下,某班有45名同学全部参加体验,购票总费用不超过1700元,那么最多有多少名同学选择“空中飞人”体验项目?