福建省福州市平潭综合实验区2022-2023学年七年级下学期数学期末试题
试卷更新日期:2023-09-28 类型:期末考试
一、单选题
-
1. 2的平方根为( )A、4 B、±4 C、 D、±2. 如图,直线AC和直线BD相交于点O,若∠1+∠2=70°,则∠BOC的度数是( ).
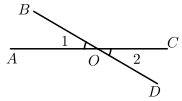 A、100° B、115° C、135° D、145°3. 下列方程是二元一次方程的是( )A、x-xy=1 B、x2-y-2x=1 C、3x-y=1 D、-2y=14. 下列不等式中,属于一元一次不等式的是( )A、 B、 C、 D、5. 下列调查方式,最适合全面调查的是( )A、检测某品牌鲜奶是否符合食品卫生标准 B、了解某班学生一分钟跳绳成绩 C、了解北京市中学生视力情况 D、调查某批次汽车的抗撞击能力6. 下列命题中,是假命题的是( )A、如果两个角相等,那么它们是对顶角 B、同旁内角互补,两直线平行 C、如果 , , 那么 D、负数没有平方根7. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间8. 北京成功举办了2022年冬奥会,吉祥物冰墩墩深受人们的喜爱,下面四个图案可以看作由“如图的冰墩墩”经过平移得到的是( )
A、100° B、115° C、135° D、145°3. 下列方程是二元一次方程的是( )A、x-xy=1 B、x2-y-2x=1 C、3x-y=1 D、-2y=14. 下列不等式中,属于一元一次不等式的是( )A、 B、 C、 D、5. 下列调查方式,最适合全面调查的是( )A、检测某品牌鲜奶是否符合食品卫生标准 B、了解某班学生一分钟跳绳成绩 C、了解北京市中学生视力情况 D、调查某批次汽车的抗撞击能力6. 下列命题中,是假命题的是( )A、如果两个角相等,那么它们是对顶角 B、同旁内角互补,两直线平行 C、如果 , , 那么 D、负数没有平方根7. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间8. 北京成功举办了2022年冬奥会,吉祥物冰墩墩深受人们的喜爱,下面四个图案可以看作由“如图的冰墩墩”经过平移得到的是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 劳动委员统计了某周全班同学的家庭劳动次数(单位:次),按劳动次数分为4组: , , , , 绘制成如图所示的频数分布直方图.从中任选一名同学,则该同学这周家庭劳动次数不足6次的概率是( )
9. 劳动委员统计了某周全班同学的家庭劳动次数(单位:次),按劳动次数分为4组: , , , , 绘制成如图所示的频数分布直方图.从中任选一名同学,则该同学这周家庭劳动次数不足6次的概率是( )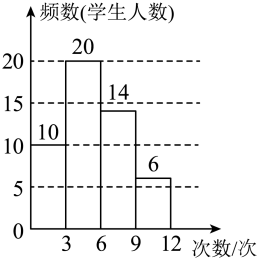 A、 B、 C、 D、10. 如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3 , 第4次向右跳动3个单位至点P4 , 第5次又向上跳动1个单位至点P5 , 第6次向左跳动4个单位至点P6 , ….照此规律,点P第100次跳动至点P100的坐标是( )
A、 B、 C、 D、10. 如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3 , 第4次向右跳动3个单位至点P4 , 第5次又向上跳动1个单位至点P5 , 第6次向左跳动4个单位至点P6 , ….照此规律,点P第100次跳动至点P100的坐标是( )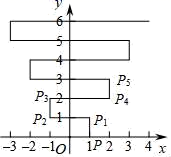 A、(﹣26,50) B、(﹣25,50) C、(26,50) D、(25,50)
A、(﹣26,50) B、(﹣25,50) C、(26,50) D、(25,50)二、填空题
-
11. 不等式 的解集是 .12. 比较大小:(选填“>”、“=”、“<”).13. 如图, 与 都相交, ,则 .
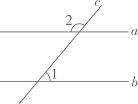 14. 把命题“对顶角相等”改写成“如果……,那么……”的形式为 .15. 直角坐标系中,点在第二象限,且到轴和轴的距离分别为 , , 则点的坐标为 .16. 在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为 .
14. 把命题“对顶角相等”改写成“如果……,那么……”的形式为 .15. 直角坐标系中,点在第二象限,且到轴和轴的距离分别为 , , 则点的坐标为 .16. 在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为 .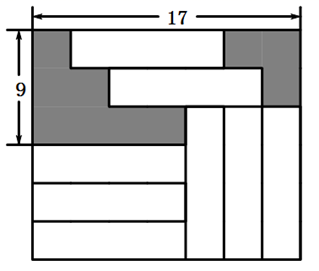
三、解答题
-
17. 计算:18. 解方程组: .19. 解不等式组: .20. 完成下面的证明:如图,AB 和CD相交于点O,AC//BD,∠A=∠AOC.求证∠B=∠BOD.
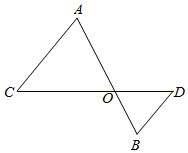
证明:∵AC//BD(已知)
∴∠A=∠B( ).
∵∠A=∠AOC(已知)
∴∠B=∠AOC( ).
∵∠AOC=∠ ▲ ( ).
∴∠B=∠BOD(等量代换).
21. 为了解某市初中学生课外阅读情况,调查小组对该市这学期初中学生阅读课外书籍的册数进行了抽样调查,并根据调查结果绘制成如下统计图.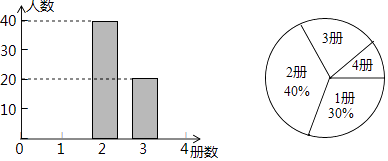
根据统计图提供的信息,解答下列问题:
(1)、本次抽样调查的样本容量是;(2)、补全条形统计图;(3)、该市共有12000名初中生,估计该市初中学生这学期课外阅读超过2册的人数.
22. 如图,在直角坐标系xOy中,已知A , B , C三点的坐标分别为 , , . (1)、把三角形ABC向右平移4个单位长度,得到三角形 , 再向上平移5个单位长度,得到三角形 , 画出三角形和三角形;(2)、写出平移后三角形的各顶点的坐标.23. 国家实行一系列“三农”优惠政策后,使农民收入大幅度增加,也调动了农民生产积极性.某农业基地去年种植蔬菜和茶叶的总收入是万元,今年扩大了蔬菜和茶叶的种植面积,这样按照去年的平均每亩收入,预计今年蔬菜和茶叶的种植总收入将比去年增加万元,其中蔬菜的种植收入将增加 , 茶叶种植收入将增加 .(1)、问该农业基地去年种植蔬菜和茶叶的收入各是多少万元?(2)、经测算茶叶平均每亩的收入要比蔬菜平均每亩的收入多万元,日常管理中,蔬菜平均每亩需人管理,茶叶平均每亩需人管理.若今年新增的管理蔬菜和茶叶的人数比为: , 问该农业基地管理蔬菜和茶叶今年共需新增多少人?24. 先阅读下面的文字,然后解答问题.
(1)、把三角形ABC向右平移4个单位长度,得到三角形 , 再向上平移5个单位长度,得到三角形 , 画出三角形和三角形;(2)、写出平移后三角形的各顶点的坐标.23. 国家实行一系列“三农”优惠政策后,使农民收入大幅度增加,也调动了农民生产积极性.某农业基地去年种植蔬菜和茶叶的总收入是万元,今年扩大了蔬菜和茶叶的种植面积,这样按照去年的平均每亩收入,预计今年蔬菜和茶叶的种植总收入将比去年增加万元,其中蔬菜的种植收入将增加 , 茶叶种植收入将增加 .(1)、问该农业基地去年种植蔬菜和茶叶的收入各是多少万元?(2)、经测算茶叶平均每亩的收入要比蔬菜平均每亩的收入多万元,日常管理中,蔬菜平均每亩需人管理,茶叶平均每亩需人管理.若今年新增的管理蔬菜和茶叶的人数比为: , 问该农业基地管理蔬菜和茶叶今年共需新增多少人?24. 先阅读下面的文字,然后解答问题.大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是 , 将这个数减去其整数部分,差就是小数部分.
由此我们还可以得到一个真命题:
如果 , 其中是整数,且 , 那么 , .
请解答下列问题:
(1)、如果 , 其中是整数,且 , 那么 , ;(2)、已知 , 其中是整数,且 , 求的值.25. 如图①,E是直线 , 内部一点, , 连接 .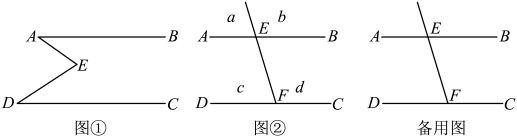 (1)、探究猜想:
(1)、探究猜想:①若 , 则 ▲ .
②猜想图①中 , , 的关系,并用两种不同的方法证明你的结论(可以用三角形内角和等于180度).
(2)、拓展应用:如图②,射线与交于分别交于点E、F , , a , b , c , d分别是被射线隔开的4个区域(不含边界,其中区域a , b位于直线上方,P是位于以上四个区域上的点,猜想:的关系.