黑龙江省佳木斯市五中联考2023-2024学年八年级上学期数学开学考试试题

试卷更新日期：2023-09-28 类型：开学考试

进入出卷网下载

一、单选题

1. 化简 $\pm \sqrt{36}$ 的值为（）

A、 $+ 6$ B、 $\pm 4$ C、 $- 6$ D、 $\pm 6$

查看试题解析
2. 点C在x轴的上方，y轴的左侧，距离x轴3个单位长度，距离y轴5个单位长度，则点C的坐标为（）

A、 $(- 3 ， 5)$ B、 $(3 ， - 5)$ C、 $(5 ， - 3)$ D、 $(- 5 ， 3)$

查看试题解析
3. 如图，给出下列条件.① $∠ 3 = ∠ 4$ ；② $∠ 1 = ∠ 2$ ；③ $∠ 4 + ∠ B C D = 180 °$ ，且 $∠ D = ∠ 4$ ；④ $∠ 3 + ∠ 5 = 180 °$ 其中，能推出 $A D ∥ B C$ 的条作为（）

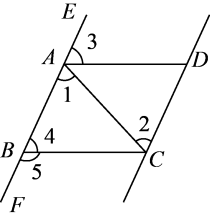A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
4. 下面调查方式中，合适的是（）

A、试航前对我国第一艘国产航母各系统的检查，选择抽样调查方式 B、了解一批袋装食品是否含有防腐剂，选择普查方式 C、为有效控制“新冠疫情”的传播，对国外入境人员的健康状况，采用普查方式 D、调查某新型防火材料的防火性能，采用普查的方式

查看试题解析
5. 判断命题“如果 $n < 1$ ，那么 $n^{2} - 1 < 0$ ”是假命题，只需举出一个反例，反例中的n可以为（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、0 D、 $- 2$

查看试题解析
6. 下列说法不正确的是（）

A、如果 $a < b$ ，那么 $- a > - b$ B、由 $- \frac{1}{2} x < y$ 可得 $x > - 2 y$ C、不等式 $x \leq 9$ 的解一定是不等式 $x < 10$ 的解 D、若 $a < b$ ，则 $a c^{2} > b c^{2}$

查看试题解析
7. 已知二元一次方程组 ${\begin{array}{l} 5 m + 4 n = 200 ① \\ 4 m - 5 n = 8 ② \end{array}$ ，如果用加减法消去n，则下列方法可行的是（）

A、①×4+②×5 B、①×5+②×4 C、①×5﹣②×4 D、①×4﹣②×5

查看试题解析
8. 如果不等式组 ${\begin{array}{l} \frac{x}{3} < 1 - \frac{x - 3}{6} \\ x < m \end{array}$ 的解集是 $x < 3$ ，那么 $m$ 的取值范围是（）

A、 $m < \frac{7}{8}$ B、 $m \geq \frac{7}{8}$ C、 $m > 3$ D、 $m \geq 3$

查看试题解析
9. 下列命题中：①同旁内角互补，两直线平行；②无理数都是无限不循环小数；③经过一点有且只有一条直线与已知直线平行；④如果一个数的立方根是这个数本身，那么这个数是0或1，是真命题的个数有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 一张长方形纸条按如图所示折叠， $E F$ 是折痕，若 $∠ E F B = 40 °$ ，则：① $∠ G E F = 40 °$ ；② $∠ E G B = 70 °$ ；③ $∠ A E G = 100 °$ ；④ $∠ C F C^{'} = 80 °$ ．以上结论正确的有（）

A、①③④ B、②③④ C、①②③ D、①②

查看试题解析

二、填空题

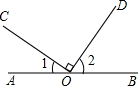
11. 如图，点O为直线AB上一点，OC⊥OD ，如果∠1＝35°，那么∠2的度数是；

查看试题解析
12. 如图，将 $△ D E F$ 沿 $F E$ 方向平移 $3 c m$ 得到 $△ A B C$ ，若 $△ D E F$ 的周长为 $20 c m$ ，则四边形 $A B F D$ 的周长为．

查看试题解析
13. 已知 $2 x - y = 4$ ，用含x的代数式表示y为： $y =$ ．

查看试题解析
14. 已知方程组 ${\begin{array}{l} 3 x + y = 1 + 3 m \\ x + 3 y = 1 - m \end{array}$ 的解满足 $x + y < 0$ ，则 $m$ 取值范围是．

查看试题解析
15. 若点N的坐标为 $(a ， 2 a - 1)$ ，则点N一定不在第象限．

查看试题解析
16. 已知关于 $x$ 的方程： $x - \frac{2 - a x}{6} = \frac{x}{3} - 1$ 有非负整数解，则整数 $a$ 的所有可能的值之和为．

查看试题解析
17. 已知关于 $x$ 、 $y$ 的方程 $x^{2} m^{2} - x^{2} + (m + 1) y + 2 x = 6$ 是二元一次方程，则 $m =$ ．

查看试题解析
18. 若不等式组 ${\begin{array}{l} 2 x - 4 > 0 \\ x < m \end{array}$ 无解，则m的取值范围是．

查看试题解析
19. 关于 $x$ 、 $y$ 的二元一次方程 $2 x + 5 y = 17$ 的非负整数解是．

查看试题解析
20. 如图，动点 $P$ 在平面直角坐标系中按图中箭头所示方向运动，第 $1$ 次从原点运动到点 $(- 1 ， 1)$ ，第 $2$ 次接着运动到点 $(- 2 ， 0)$ ，第 $3$ 次接着运动到点 $(- 3 ， 2)$ ， ……，按这样的运动规律，经过第 $2025$ 次运动后，动点 $P$ 的坐标是．

查看试题解析

三、解答题

21. 计算： $- 2^{3} + | - \sqrt{16} + \sqrt[3]{- 27} | \times \frac{1}{- 7^{2}} + \sqrt{{(- 6)}^{2}}$ ．

查看试题解析
22. 解方程组： ${\begin{array}{l} 2 y - x = 2 \\ \frac{x}{2} - \frac{y}{3} = 1 \end{array}$ ．

查看试题解析
23. 解不等式组： ${\begin{array}{l} 3 x - \frac{x}{2} \geq 5 \\ \frac{x - 1}{2} - \frac{x}{3} \leq 1 \end{array}$ 并把它的解集在数轴上表示出来．

查看试题解析

24. 在2020年为了调查五中学生对“新型冠状病毒”的知识了解程度，我校在学生中做了一次抽样调查，调查结果共分为四个等级：A ．非常了解；B ．比较了解；C ．基本了解；D ．不了解．根据调查统计结果，绘制了不完整的三种统计图表.请结合统计图表，回答下列问题．

如下是对病毒了解程度的统计表：

对病毒的了解程度	A ．非常了解	B ．比较了解	C ．基本了解	D ．不了解
百分比	$5 %$	$m$	$45 %$	$n$

(1)、本次参与调查的学生共有人，

m =

，

n =

；

(2)、图2所示的扇形统计图中

D

和

B

部分扇形所对应的圆心角度数之差是

°

；

(3)、请补全图1的条形统计图；

(4)、若我校有学生3500人，根据样本估计全校对病毒“不了解”的学生约是多少人？

查看试题解析

25. 已知直线 $A B ∥ C D$ ， $O F$ 平分 $∠ B O D$ 且 $O E ⊥ O F$ ， $∠ B = 58 °$ ，求 $∠ C O E$ 的度数．

查看试题解析
26. 佳木斯市决定购置一批共享单车，经过市场调查发现：购买3辆电动单车与4辆脚踏单车花费相同；购买5辆电动单车与4辆脚踏单车共花费16000元．

(1)、求每辆电动单车和脚踏单车的单价？

(2)、佳市经济开发部门决定，先在市内某一社区配发共享单车；要求在这社区内配发电动单车比脚踏单车多4辆；且两种单车的总和至少需要24辆，要购置这两种共享单车的费用不超过50000元；问：该社区有哪几种购车方案？采用哪种方案所需费用最低？最低费用是多少元？

查看试题解析
27. 在平面直角坐标系中，点 $A$ 、 $B$ 的坐标分别为 $A (a ， 0)$ ， $B (0 ， b)$ 且 $a$ ， $b$ 满足 $| a + 3 | = - \sqrt{b + 1}$ ，已知点 $C$ 坐标为 $(0 ， 4)$ ，

(1)、求 $a$ 、 $b$ 的值及 $S_{△ A B C}$ 的面积；

(2)、若点 $M$ 在坐标轴上，且 $S_{△ A C M} = \frac{1}{5} S_{△ A B C}$ ，请直接写出点 $M$ 的坐标．

查看试题解析