广西壮族自治区南宁市邕宁区2022-2023学年八年级下学期数学期末试题

试卷更新日期：2023-09-28 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\sqrt{x}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x > 0$ B、 $x \geq 0$ C、 $x < 0$ D、 $x \leq 0$

查看试题解析
2. 下列各图象中，表示 $y$ 是 $x$ 的函数的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各组数为边长能构成直角三角形的是（）

A、1，2，3 B、2，3，4 C、1，1， $\sqrt{2}$ D、6，8，11

查看试题解析
4. 某鞋店销售同种品牌不同尺码的男鞋，采购员再次进货时，对于男鞋的尺码，他最关注的是（　　）

A、方差 B、众数 C、中位数 D、平均数

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{8} - \sqrt{2} = 2$ B、 $\sqrt{13} + \sqrt{3} = \sqrt{16} = 4$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{8} \div \sqrt{2} = 4$

查看试题解析
6. 把两块形状大小完全相同的含有45°角的三角板的一边拼在一起，则所得到的图形不可能有（）

A、正方形 B、等边三角形 C、等腰直角三角形 D、平行四边形（非矩形、菱形、正方形）

查看试题解析
7. 八年级某班甲、乙、丙、丁四位同学准备选一人参加学校“跳绳”比赛．经过三轮测试，他们的平均成绩都是每分钟 $180$ 个，方差分别是 $S_{甲}^{2} = 65 ， S_{乙}^{2} = 56.5 ， S_{丙}^{2} = 53 ， S_{丁}^{2} = 50.5$ ，你认为派哪一个同学去参赛更合适（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 如图，矩形ABCD中，对角线AC ， BD交于点O ．若∠AOB＝60°，BD＝6，则AB的长为（）．

A、4 B、4 $\sqrt{3}$ C、3 D、5

查看试题解析
9. 把函数y＝x的图象向上平移2个单位，下列各点在平移后的函数图象上的是（）

A、（2，2） B、（2，3） C、（2，4） D、（2，5）

查看试题解析
10. 某汽车在某一直线道路上行驶，该车离出发地的距离 $s$ （千米）和行驶时间 $t$ （小时）之间的函数关系如图所示（折线 $A B C D E$ ）．根据图中提供的信息，下列说法正确的是（）

A、汽车共行驶了120千米； B、汽车在行驶途中停留了2小时； C、汽车在行驶过程中的平均速度为 $\frac{80}{3}$ 小时/千米； D、汽车自出发后3小时至4.5小时之间行驶的速度不变．

查看试题解析
11. 如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8 m处，发现此时绳子末端距离地面2 m，则旗杆的高度(滑轮上方的部分忽略不计)为（）

A、12 m B、13 m C、16 m D、17 m

查看试题解析
12. 对于函数 $y = - 5 x + 1$ ，下列结论：①它的图象必经过点 $(- 1 ， 5)$ ②它的图象经过第一、二、四象限 ③当 $x > 1$ 时， $y < 0$ ④ $y$ 的值随 $x$ 值的增大而增大，其中正确的个数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

13. 化简： $\sqrt{9}$ = ．

查看试题解析
14. 已知，如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距．

查看试题解析
15. 已知点 $(- 2 ， m) ， (3 ， n)$ 都在直线 $y = - \sqrt{2} x + b$ 上，则 $m$ $n$ ．（填“ $>$ ”“ $<$ ”或“ $=$ ”）

查看试题解析
16. 小颖同学参加学校举办的“抗击疫情，你我同行”主题演讲比赛，她的演讲内容、语言表达和形象风度三项得分分别为86分、90分、80分，若这三项依次按照50%，40%，10%的百分比确定成绩，则她的成绩为.

查看试题解析
17. 若函数 $y = a x$ 和函数 $y = b x + c$ 的图象如图所示，则关于 $x$ 的不等式 $a x - b x \geq c$ 的解集是．

查看试题解析
18. 如图，在平面直角坐标系中，点 $A_{1}$ 的坐标为 $(1 ， 2)$ ，以点 $O$ 为圆心，以 $O A_{1}$ 长为半径画弧，交直线 $y = \frac{1}{2} x$ 于点 $B_{1}$ ，过点 $B_{1}$ 作 $B_{1} A_{2} ∥ y$ 轴，交直线 $y = 2 x$ 于点 $A_{2}$ ，以点 $O$ 为圆心，以 $O A_{2}$ 长为半径画弧，交直线 $y = \frac{1}{2} x$ 于点 $B_{2}$ ；过点 $B_{2}$ 作 $B_{2} A_{3} ∥ y$ 轴，交直线 $y = 2 x$ 于点 $A_{3}$ ，以点 $O$ 为圆心，以 $O A_{3}$ 长为半径画弧，交直线 $y = \frac{1}{2} x$ 于点 $B_{3}$ ；过 $B_{3}$ 点作 $B_{3} A_{4} ∥ y$ 轴，交直线 $y = 2 x$ 于点 $A_{4}$ ，以点 $O$ 为圆心，以 $O A_{4}$ 长为半径画弧，交直线 $y = \frac{1}{2} x$ 于点 $B_{4}$ ， …，按照如此规律进行下去，点 $B_{2023}$ 的坐标为．

查看试题解析

三、解答题

19. 计算： $(- 1)^{2023} - | 1 - \sqrt{3} | + \sqrt{6} \times \sqrt{\frac{1}{2}}$ ．

查看试题解析
20. 先化简，再求值： $\frac{a^{2} - b^{2}}{a} \div (a + \frac{2 a b + b^{2}}{a})$ ，其中 $a = \sqrt{2} + 1 ， b = \sqrt{2} - 1$ ．

查看试题解析
21. 如图， $A C ⊥ B C ， A C = B C = B D = 1 ， A D = \sqrt{3}$ ．

(1)、求 $A B$ 的长；

(2)、求 $△ A D B$ 的面积．

查看试题解析
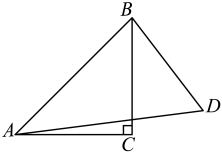22. 为比较营养液 $A$ 和营养液 $B$ 对某种小西红柿产量的影响，甲、乙两个生物小组各选取了10株长势相近的小西红柿秧苗进行对照实验．甲组使用营养液 $A$ ，乙组使用营养液 $B$ ．将每株的产量记录整理，并绘制了如下两个条形图．

解答下列问题：

(1)、甲组产量的中位数为，乙组每株产量的众数为；

(2)、为了使产量更稳定，请计算两组产量的平均数，再结合条形图，则应选择营养液；（填“ $A$ ”或“ $B$ ”）；

(3)、产量30个及以上为秧苗长势良好．现在选用第（2）问推荐的营养液培育1000株秧苗，请估计长势良好的大约有多少株？

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，以B为圆心， $B C$ 为半径画弧，交线段 $A B$ 于点 $D$ ，以A为圆心， $A D$ 为半径画弧，交线段 $A C$ 于点 $E$ ．

(1)、若 $∠ A = 26 °$ ，求 $∠ A C D$ 的度数；

(2)、若 $B C = 8 c m ， C E = 6 c m$ ，求 $A D$ 的长．

查看试题解析

24.

A 、 B

两个水果市场各有芒果15吨，现从

A 、 B

向甲、乙两地运送芒果，其中甲地需要芒果16吨，乙地需要芒果14吨，从

A

到甲地的运费为50元/吨，到乙地的运费为30元/吨，从

B

到甲地的运费为60元/吨，到乙地的运费为45元/吨．

(1)、设

A

地到甲地运送芒果

x

吨，请完成下表：

	调往甲地（单位：吨）	调往乙地（单位：吨）
A	$x$	①
B	②	③

(2)、设总运费为

y

元，请写出

y

与

x

的函数关系式，并直接写出

x

的取值范围．

(3)、怎样调送芒果才能使运费最少？

查看试题解析

25. 把一张矩形纸片 $A B C D$ 按如图方式折叠，使顶点 $B$ 和点 $D$ 重合，折痕为 $E F$ ．若 $A B = 6 c m ， B C = 8 c m$ ．

(1)、求线段 $D F$ 的长；

(2)、连接 $B E$ ，求证：四边形 $B F D E$ 是菱形；

(3)、求线段 $E F$ 的长．

查看试题解析
26. 已知直线 $l$ 为 $x + y = 8$ ，点 $P (x ， y)$ 在 $l$ 上，且 $x > 0 ， y > 0$ ，点 $A$ 的坐标为 $(4 ， 0)$ ．

(1)、设 $△ O A P$ 的面积为 $S$ ，求 $S$ 与 $x$ 的函数关系式，并直接写出 $x$ 的取值范围；

(2)、当 $S = 10$ 时，求点 $P$ 的坐标；

(3)、在直线 $l$ 上有一点 $M$ ，使 $O M + M A$ 的和最小，求点 $M$ 的坐标．

查看试题解析